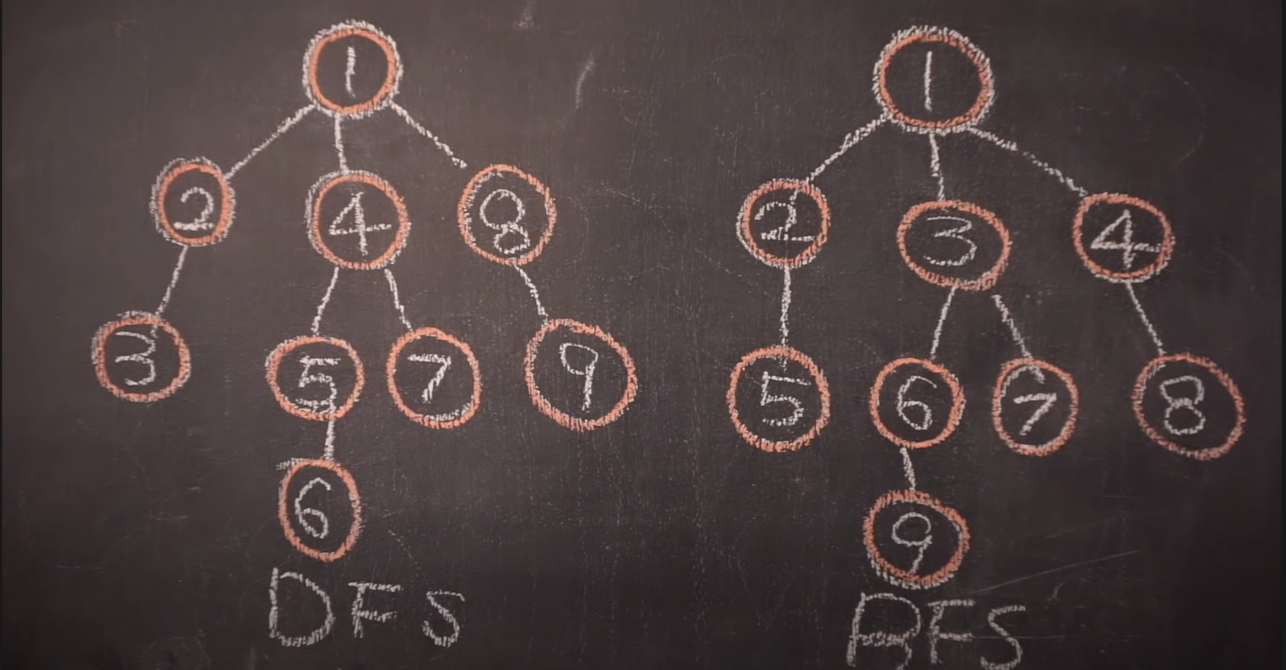
섹션2에서 잘 모르고 넘어갔던 BFS와 DFS가 내일 알고리즘 시간에 나오던데 다시 짚어 보기로 했다.
DFS와 BFS는 모두 노드 수+간선 수만큼의 복잡도를 지닌다. 즉, O(n)
BFS 구조는 두 개의 큐를 활용하는데, DFS는 한 개의 스택과 한 개의 큐를 사용한다는 차이가 있음
BFS 구조는 이전 노드와 연결된 노드들을 먼저 탐색해야 하기 때문에 queue,
DFS는 이전 노드가 아니라 자기 자신과 연결되었던 노드들 먼저 탐색하기 때문에 stack을 사용한다.
DFS
DFS는 Depth-First Search의 약자로 깊이 우선 탐색이라고 한다.
한 정점에서 시작해서 다음 경로로 넘어가기 전에 해당 경로를 완벽하게 탐색할 때 사용한다.
전위 순회(Preorder), 중위 순회(Inoder), 후위 순회(Postorder)가 DFS에 속한다.
DFS는 시작점에서 인접 노드를 방문하고 그 인접 노드의 인접 노드로 쭉 파고들다
마지막까지 방문했다면 형제 노드를 방문하는 검색 방법이다.
DFS는 Stack과 Queue를 이용해서 구현한다.
진행 순서
DFS를 진행할때에는 Stack을 하나 만들고, 시작 노드를 Stack에 담아두어 시작한다.
탐색을 마친 노드를 담아줄 Queue도 하나 만든다.
-
시작 노드를 Stack에서 꺼내고 그 노드의 인접 노드들을 Stack에 담아준다.
-
꺼낸 노드를 탐색을 마친 Queue에 담아준다.
-
Stack의 특성을 따라 마지막 인덱스에 위치한 노드를 꺼내 탐색을 마친 Queue에 담아준다.
-
꺼낸 노드의 인접 노드들을 Stack에 담아준다.
-
이때 이미 Stack에 담겨 있거나 출력 된 노드는 생략한다.
-
모든 노드를 순회하면 종료한다.
const graph = {
A: ["B", "C"],
B: ["A", "D"],
C: ["A", "G", "H", "I"],
D: ["B", "E", "F"],
E: ["D"],
F: ["D"],
G: ["C"],
H: ["C"],
I: ["C", "J"],
J: ["I"],
};
// (graph, 시작 정점)
const dfs = (graph, startNode) => {
let needVisitStack = []; // 탐색을 해야 할 노드들
let visitedQueue = []; // 탐색을 마친 노드들
needVisitStack.push(startNode);
// 탐색을 해야 할 노드가 남아 있다면
while (needVisitStack.length !== 0) {
const node = needVisitStack.pop();
if (!visitedQueue.includes(node)) {
visitedQueue.push(node);
needVisitStack = [...needVisitStack, ...graph[node]];
}
}
return visitedQueue;
};
console.log(dfs(graph, "A"));
// ["A", "C", "I", "J", "H", "G", "B", "D", "F", "E"]출처 : https://ryusm.tistory.com/48
BFS
BFS는 Breadth-First Search의 약자로 너비 우선 탐색이라고 한다.
주로 두 정점 사이의 최단 경로를 찾을 때 사용한다.
BFS는 시작점에서 인접 노드들을 방문하여 모두 방문한뒤 인접 노드를 방문하는 레벨 단위 검색 방식이다.
BFS는 Queue를 이용해서 구현한다.
진행순서
BFS를 진행할때에는 Queue을 하나 만들고, 시작 노드를 Stack에 담아두어 시작한다.
탐색을 마친 노드를 담아줄 Queue도 하나 만든다.
-
시작 노드를 Queue에서 꺼내고 꺼낸 노드의 인접 노드들을 Queue에 담아준다.
-
꺼낸 노드를 탐색을 마친 노드에 담아준다.
-
Queue의 특성을 따라 가장 앞 인덱스에 위치한 노드를 꺼낸다.
-
꺼낸 노드의 인접 노드들을 Queue에 담아준다.
-
이때 이미 Queue에 담겨 있거나 출력 된 노드는 생략한다.
-
모든 노드를 순회하면 종료한다.
const graph = {
A: ["B", "C"],
B: ["A", "D"],
C: ["A", "G", "H", "I"],
D: ["B", "E", "F"],
E: ["D"],
F: ["D"],
G: ["C"],
H: ["C"],
I: ["C", "J"],
J: ["I"]
};
const bfs = (graph, startNode) => {
let visited = []; // 탐색을 마친 노드들
let needVisit = []; // 탐색해야할 노드들
needVisit.push(startNode); // 노드 탐색 시작
while (needVisit.length !== 0) { // 탐색해야할 노드가 남아있다면
const node = needVisit.shift(); // queue이기 때문에 선입선출, shift()를 사용한다.
if (!visited.includes(node)) { // 해당 노드가 탐색된 적 없다면
visited.push(node);
needVisit = [...needVisit, ...graph[node]];
}
}
return visited;
};
console.log(bfs(graph, "A"));
// ["A", "B", "C", "D", "G", "H", "I", "E", "F", "J"]출처 : https://ryusm.tistory.com/48
참고 사이트
https://www.youtube.com/watch?v=_hxFgg7TLZQ
https://ryusm.tistory.com/48
