부스트캠프 AI Tech 3기(week1) Day1

정재욱·2022년 1월 17일

목록 보기

2/30

드디어 부스트캠프 AI Tech 3기가 오늘 시작했습니다.
코어타임은 10시부터 오후 7시까지 입니다. 오늘은 첫 날이라 10시부터 1시간동안 오리엔테이션을 진행했고, 11시부터 12시까지 앞으로 약 7주간 같이 공부할 피어들을 만나는 MeetUP이 진행되었습니다.

처음 만나는 자리라서 다들 어색했고... 피어 한분이 개인사정으로 인하여 참여하지 못해서 4명이서 같은 팀이 되었습니다. 하지만 팀원분들이 다들 먼저 대화를 유도해주셔서 어색함이 많이 풀린 것 같습니다. 저는 개인적으로 피어분들이 매우 좋은것 같아요ㅎㅎ.
저희는 간단하게 자기소개를 진행하고 앞으로 우리 팀이 학습을 하는데 있어서 필요한 그라운드룰을 정했습니다.

이번주는 과목이 Python Basics for AI과 AI Math가 있는데, AI Math는 하루에 2강, Python Basics for AI는 각자 들을 수 있을만큼 듣기로 했습니다. Python Basics for AI는 Pre-course에서 들은 강의가 대부분이라 초반에는 회고를 하지 않고 중반부터 회고를 하겠습니다.

📌 (AI Math 1강) 벡터가 뭐에요?

✍벡터가 뭔가요?

벡터는 숫자를 원소로 가지는 리스트(list) 또는 배열(array)입니다.
벡터는 공간에서 한 점을 나타냅니다.
벡터는 원점으로부터 상대적 위치를 표현합니다.
벡터에 숫자를 곱해주면 길이만 변합니다. 이를 스칼라곱이라 부릅니다.
- aX에서 a < 1 이면 길이가 줄어들고, a > 1 이면 길이가 늘어납니다.
- 단, 0보다 작으면 반대 방향이 됩니다.
벡터끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있습니다.
벡터끼리 같은 모양을 가지면 성분곱(Hadamard product)을 계산할 수 있습니다. element-wise product라고도 합니다. 기호로는 ⊙로 표시합니다.

✍벡터의 덧셈, 뺄셈을 알아보자

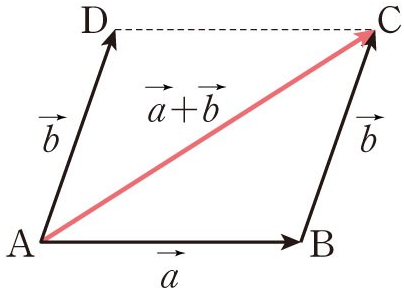
두 벡터의 덧셈은 다른 벡터로부터 상대적 위치이동을 표현합니다.
- 즉, 두 벡터 Y + X는 원점을 Y로 옮기는 것입니다. 그렇게 되면 Y + X는 벡터 Y로 부터 X만큼의 상대적 위치를 표현합니다.
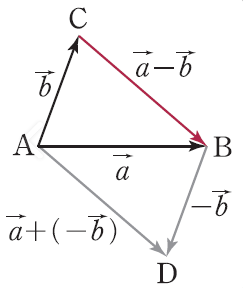
두 벡터의 뺄셈은 방향을 뒤집은 덧셈입니다.

✍벡터의 노름 구해보기

벡터의 노름(norm)은 원점에서부터의 거리를 말합니다.
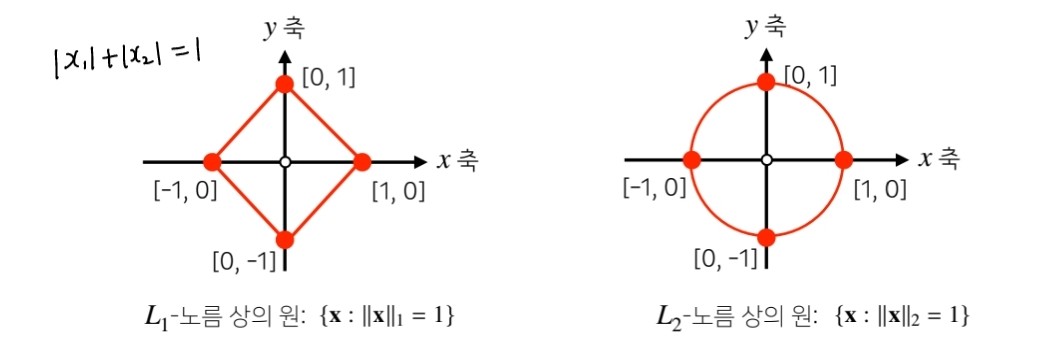
∥·∥기호는 노름(norm)이라 부릅니다.
$L_1$ -norm은 각 성분의 변화량의 절대값을 모두 더합니다.
- $∥x∥_1 = \sum_{i=1}^{d} |x_i|$
$L_2$ -norm은 피타고라스 정리를 이용해 유클리드 거리를 계산합니다.
- $∥x∥_2 = \sqrt{\sum_{i=1}^{d}{|x_i|^2}}$
- $L_2$ -norm은 np.linalg.norm을 이용해서 구현 가능합니다.
벡터의 노름은 임의의 차원 d에 대해 성립하는 것을 명심해야 합니다.

✎ 왜 다른 norm을 소개하나요?

노름의 종류에 따라 기하학적 성질이 달라지기 때문입니다.
머신러닝에서는 각 성질들이 필요할 때가 있으므로 둘 다 사용합니다.

✎ 두 벡터 사이의 거리를 구해보자

$L_1$ -norm, $L_2$ -norm을 이용해 두 벡터 사이의 거리를 계산할 수 있습니다.
두 벡서 사이의 거리를 계산할 때는 벡터의 뺄셈을 이용합니다.
뻴셈을 거꾸로 해도 거리는 같습니다.
- $∥a-b∥ = ∥b-a∥$

✎ 두 벡터 사이의 각도를 구해보자

제2 코사인 법칙에 의해 두 벡터 사이의 각도를 계산할 수 있습니다.
- $cos\theta = \frac{∥x∥^2_2+∥y∥^2_2-∥x-y∥^2_2}{2∥x∥_2∥y∥_2}$
분자를 쉽게 계산하는 방법이 있는데, 바로 내적 이용하는 것입니다.
- 내적은 정사영의 길이를 벡터 $Y$ 의 길이 $∥Y∥$ 만큼 조정한 값입니다.
- 내적은 두 벡터의 유사도(similarity)를 측정하는데도 사용 가능합니다.
- $cos\theta = \frac{2\sum^{d}_{i=1}x_iy_i}{2∥x∥_2∥y∥_2}$

📌 (AI Math 2강) 행렬이 뭐에요?

✍행렬은 뭔가요?

행렬(matrix)은 벡터를 원소로 가지는 2차원 배열입니다.
행렬은 행(row)과 열(column)이라는 인덱스(index)를 가집니다.
전치행렬(transpose matrix)은 행과 열의 인덱스가 바뀐 행렬을 말합니다.
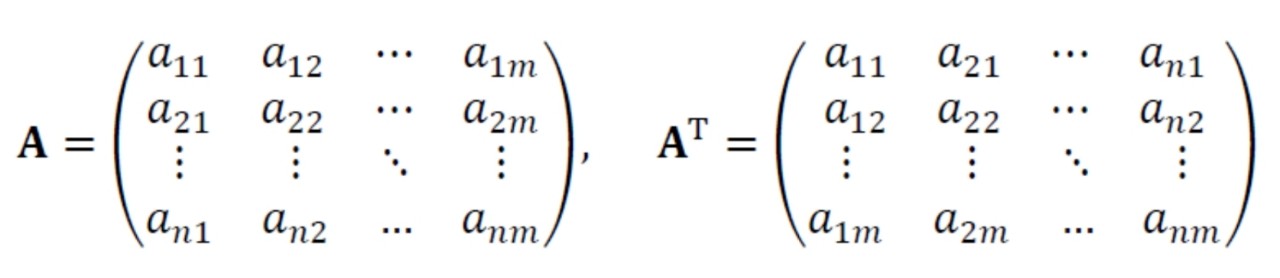
벡터가 공간에서 한 점을 의미한다면, 행렬은 여러 점들을 나타냅니다.
행렬의 행벡터 $X_i$ 는 i번째 데이터를 의미합니다.
행렬의 $x_{ij}$ 는 i번째 데이터의 j번째 변수의 값을 말합니다.

✍행렬의 덧셈, 뺄셈, 성분곱, 스칼라곱

행렬끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있습니다.
성분곱(element-wise product)은 벡터와 똑같습니다. 즉, 각 인덱스 위치끼리 곱합니다.
스칼라곱도 벡터와 차이가 없습니다.

✍행렬 곱셈

행렬 곱셉(matrix multiplication)은 i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산합니다.
- numpy 에선 @ 연산을 사용합니다.
- $XY = \left(\sum_{k} x_{ik}y_{kj}\right)$

✍행렬도 내적이 있을까?

넘파이의 np.inner는 i번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산합니다.
수학에서는 $X^TY$ 이지만, 넘파이의 np.inner은 행벡터 기준 이므로 $XY^T$ 입니다.
$XY^T = (\sum_{k}x_{ik}y_{ik})$

✍행렬은 연산자다?

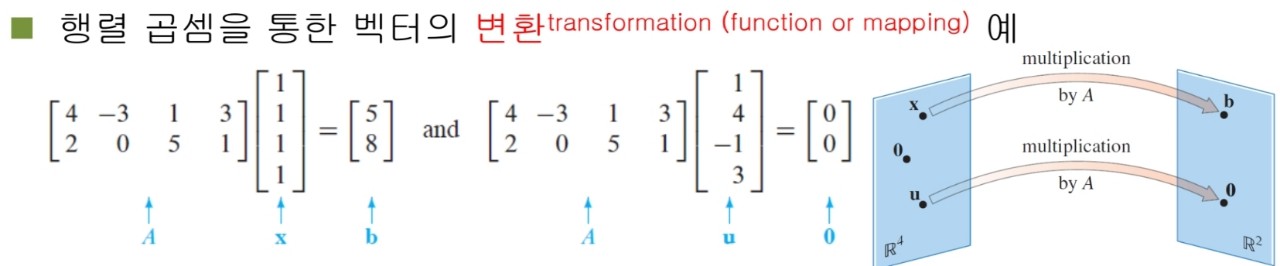
행렬은 벡터공간에서 사용되는 연산자(operator)로 이해합니다.
행렬곱을 통해서 벡터를 다른 차원의 공간으로 보낼 수 있습니다.

✍역행렬 이해하기

어떤 행렬 $A$ 의 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix)이라 부르고 $A^{-1}$ 라 표기합니다. 역행렬은 행과 열 숫자가 같고 행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있습니다.
- numpy.linalg.inv로 구할 수 있습니다.

만일 역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬 $A^+$ 을 이용합니다.
$n<=m$ 인 경우는 식의 개수가 변수 개수보다 작거나 같으므로 연립방정식을 풀 때 응용할 수 있습니다.
- 무어-펜로즈 역행렬을 이용하면 연립방정식의 해를 구할 수 있습니다.
- np.linalg.pinv로 무어-펜로즈 역행렬을 구할 수 있습니다.
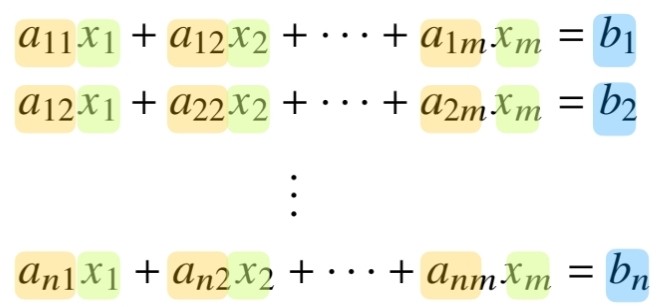
$n>=m$ 인 경우는 식의 개수가 변수 개수보다 크거나 같은 경우입니다. 이는 선형회귀분석에 사용됩니다. 왜냐하면 데이터가 변수 개수보다 많기 때문입니다.
- np.linalg.pinv를 이용하면 데이터를 선형모델(linear model)로 해석하는 선형회귀식을 찾을 수 있습니다.
- 또한 sklearn의 LinearRegression과 같은 결과를 가져올 수 있습니다.

import numpy as np 
%matplotlib inline 
import matplotlib
import matplotlib.pyplot as plt 
X = 2 * np.random.rand(100, 1)  # 0 부터 1 사이의 균일 분포에서 난수 matrix array 생성
y = 4 + 3 * X + np.random.randn(100, 1)  # random.randn : 가우시안 표준 정규 분포에서 난수 matrix array 생성
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
plt.show()

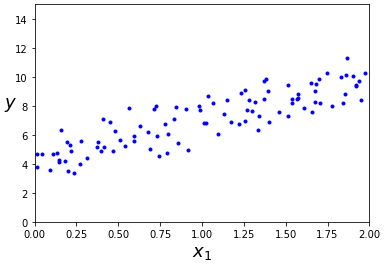데이터를 생성하기 위해 사용한 함수는 $y = 4+3x+가우시안잡음$ 입니다.
Scikit Learn과 Moore-Penrose 역행렬을 사용하여 같은 결과를 도출하는지 확인해보겠습니다.

from sklearn.linear_model import LinearRegression 
lin_reg = LinearRegression()
lin_reg.fit(X, y)          # 선형회귀 모델 훈련

# (5) lin_reg.intercept_, lin_reg.coef_ 출력 확인 
print(f"lin_reg.intercept_ : {lin_reg.intercept_}\nlin_reg.coef_  :    {lin_reg.coef_}\n")
# 각각 절편과 기울기

# (6) lin_reg.predict(X_new) 출력 확인
print(f"lin_reg.predict(X_new) : \n{lin_reg.predict(X_new)}\n")

# (7) np.linalg.pinv(X_b).dot(y) 출력 확인 
X_b = np.c_[np.ones((100, 1)), X]  # 데이터에 y절편(intercept)항 추가하기
print(f"np.linalg.pinv(X_b).dot(y) : \n{np.linalg.pinv(X_b).dot(y)}")   
# 유사역행렬을 직접 계산하여 구하기

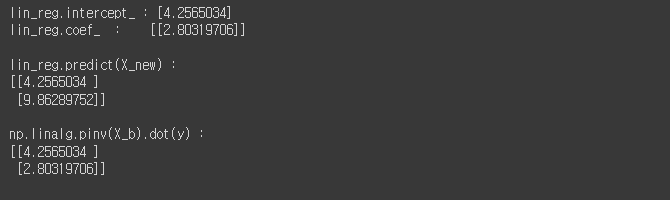위 그림을 보시면 편향과 기울기가 각각 $\theta_0 = 4$ , $\theta_1 = 3$ 와 유사하게 결과가 나온 것을 확인할 수 있습니다.
또한, Scikit Learn과 Moore-Penrose 역행렬을 이용하여 구한 결과가 서로 똑같게 나온 것을 확인할 수 있습니다.