
⭐️ LeetCode 알고리즘 풀이 (with Python)
# Implement Trie (Prefix Tree)
[Quetion]
📌 접근법
[문제 이해]
- Trie 자료구조를 class로 구현
- Trie에 문자열 삽입, 문자열 탐색, 접두사가 존재하면 True, 아니면 False
Trie 자료구조는 문자열 검색에 최적화된 자료구조이다. 주로 자동완성 기능에 많이 활용한다.
접두사 검색이 가능한데, 예를들어 apple에서 "a" 혹은 "app"등을 접두사라고 이해하면 편하다.
이 자료구조의 특징은 뿌리부터 시작해서 각각의 가지가 알파벳 문자를 표현한다는 것과 각 단어가 끝나는 지점에 특별한 표시를 해둠으로써 해당 위치 노드까지 문자열을 이루고 있음을 알린다는 것이다.
즉, 특정 문자열을 입력시 서브 트리의 리프노드까지 탐색한다는 것이다.
노드는 문자열에서 마지막 문자라는 표시인 bool값, 자식 노드를 담는 배열 혹은 해쉬 테이블로 구성된다.
의사코드로 작성하는 것보다 그림으로 표현하는게 더 이해하기 편해서 동작과정을 그림으로 표현해보았다.
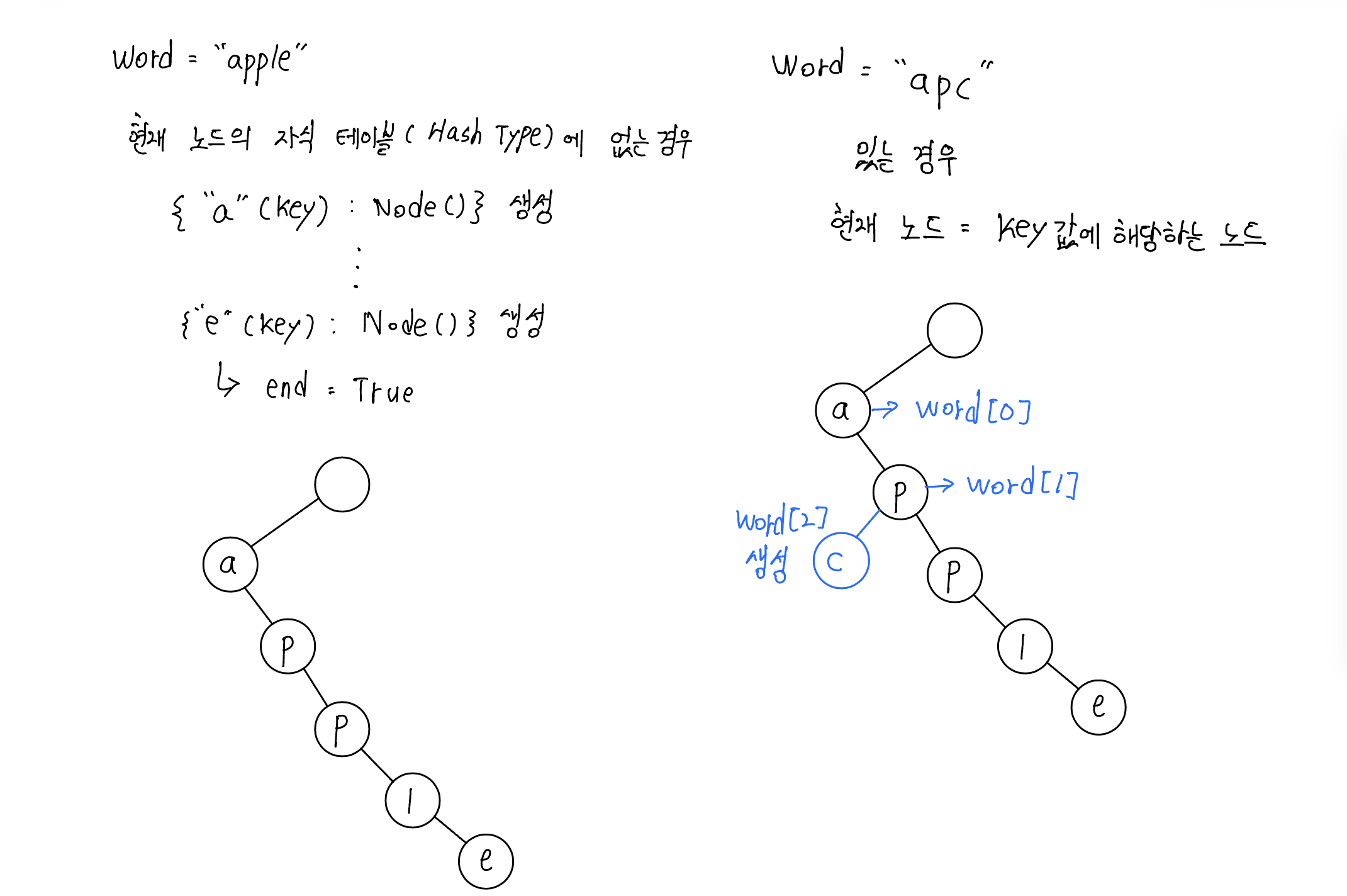
- 루트부터 찾아서 들어간다.
- 삽입의 경우, 삽입하려는 문자열을 키로 가지는 해쉬테이블이 없으면 키로 가지는 노드 생성
- 있으면 현재 노드를 다음 노드로 가르킴
- 탐색의 경우도 현재 노드 값을 기준으로 판단, 현재 노드가 end표시가 있는 문자열이면 end bool값 반환
💻 구현
# Trie의 노드
class Node:
def __init__(self):
self.children = {}
self.isEndOfWord = False
# Trie 구현 class
class Trie:
def __init__(self):
self.root = Node()
# 문자열 삽입
def insert(self, word: str) -> None:
curr = self.root
for i in word:
if i not in curr.children:
curr.children[i] = Node()
curr = curr.children[i]
curr.isEndOfWord = True
# 문자열 탐색
def search(self, word: str) -> bool:
curr = self.root
for i in word:
if i not in curr.children:
return False
curr = curr.children[i]
return curr.isEndOfWord
# 접두사 탐색
def startsWith(self, prefix: str):
curr = self.root
for i in prefix:
if i not in curr.children:
return False
curr = curr.children[i]
return TrueRuntime: 145ms | Memory: 33.9MB
LeetCode 코드 중 Runtime 79%, Memory 45% 해당하는 결과
📝 Implement Trie (Prefix Tree) 회고
-
구현한 Trie의 시간복잡도는 O(n), 공간복잡도는 O(Node의 총 개수 x Node의 크기)인데 Node 개수의 최악은 모든 문자열들의 길이 합이기 때문에 단순히 O(n)보다 훨씬 높다.
-
현재 코드는 for문으로 작성했지만 재귀적으로도 구현이 가능하고, Node의 children은 해쉬 테이블 뿐 아니라 배열로도 구현이 가능하다.
-
하지만 key값을 통한 탐색의 성능이 O(1)으로 좋다고 생각하여 해쉬 테이블인 Dictionary로 구현했다. 재귀적으로 구현해 볼 경우 성능은 같지만 코드의 복잡도 개선될 것이라고 생각한다.
# Kth Largest Element in an Array
[Quetion]
📌 접근법
[문제 이해]
- 배열에서 k번째로 큰 요소 반환
- 단, 정렬을 하지 않고 해결이 가능한지?
정렬의 방법을 사용하지 않고 k번째로 큰 요소를 반환하기 위해서는 Heap 자료구조를 활용해야한다.
Heap은 모든 부모 노드가 자식 노드보다 크거나 같은 값을 가지거나 모든 부모 노드가 자식 노드보다 작거나 같은 값을 가진다. 또한 완전 이진 트리의 형태이다.
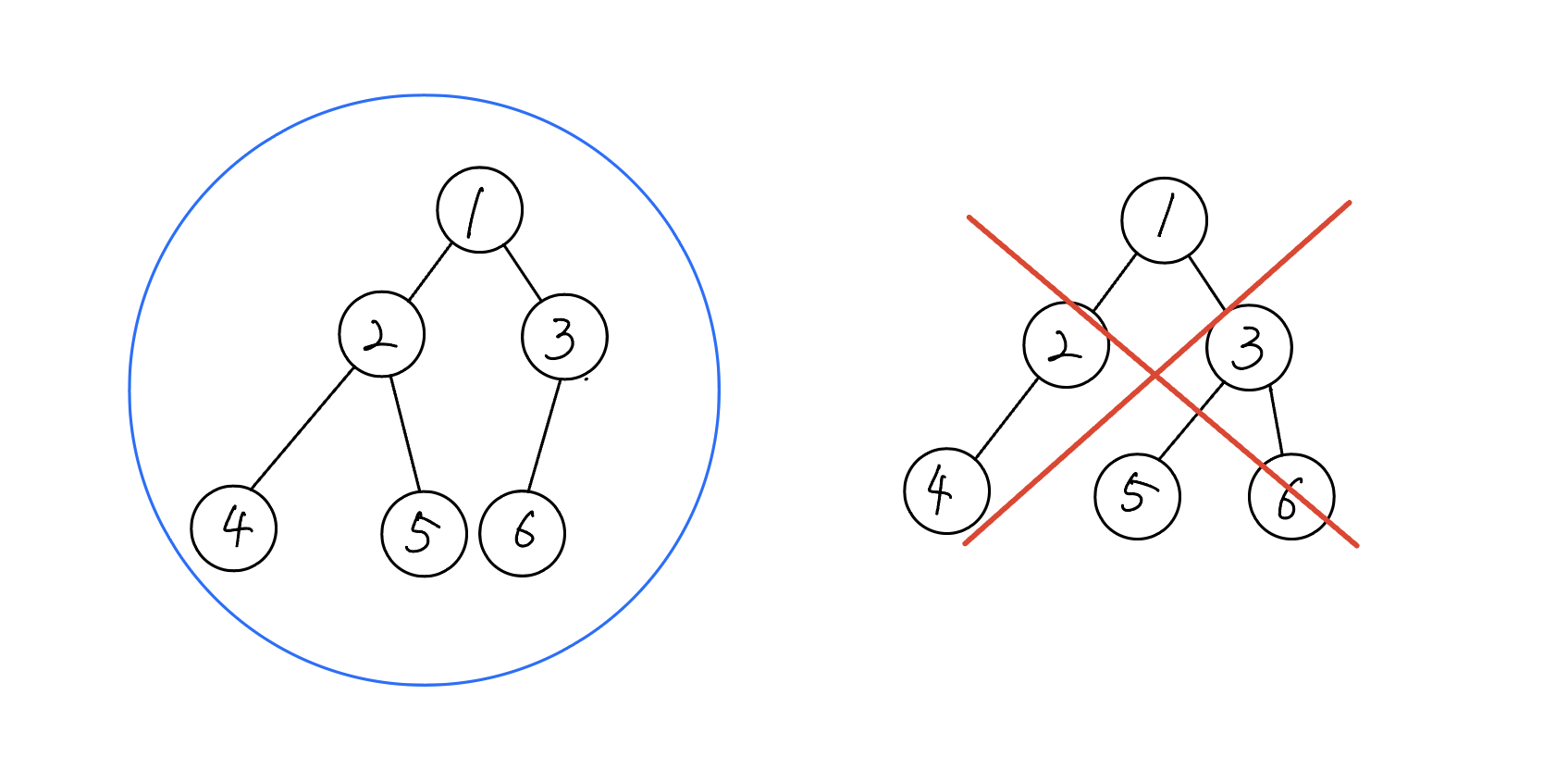 완전 이진트리는 마지막 레벨의 노드들이 왼쪽부터 차례로 채워져있는 특징과 배열로 표현이 가능하다는 특징을 가진다.
완전 이진트리는 마지막 레벨의 노드들이 왼쪽부터 차례로 채워져있는 특징과 배열로 표현이 가능하다는 특징을 가진다.
우측 그림의 노드처럼 마지막 레벨의 노드가 왼쪽 부터 채워지지 않으면 완전 이진트리라고 할 수 없다.
이번 문제는 왼쪽 그림의 노드와 같은 최소 Heap을 활용하여 주어진 배열을 Heap화 한 후, 각 하위 노드들의 값을 교체하며 정렬하는 방법으로 접근해보았다.
💻 구현
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
# 하위트리 반복 bubledown 정렬
self.bubledown(nums, len(nums), 0)
# 리프 노드 인접 값 정렬
self.childsort(nums)
return nums[k-1]
def bubledown(self, nums, n, i):
small = i
left = 2 * i + 1
right = 2 * i + 2
if left < n and nums[i] > nums[left]:
small = left
if right < n and nums[small] > nums[right]:
small = right
if small != i:
nums[i], nums[small] = nums[small], nums[i]
self.bubledown(nums, n, small)
def childsort(self, nums):
n = len(nums)
for i in range(n//2 - 1 , -1 , -1):
self.bubledown(nums, n, i)
for i in range(n-1 ,0 ,-1):
nums[i],nums[0]=nums[0],nums[i]
self.bubledown(nums, i, 0)Runtime: 2043ms | Memory: 29.6MB
LeetCode 코드 중 Runtime 5%, Memory 36% 해당하는 결과
📝 Kth Largest Element in an Array 회고
-
구현한 코드의 동작은 bubledown -> childsort를 재귀적으로 계속 반복한다.
[3, 2, 1, 5, 6, 4]의 배열을 최종 [1, 2, 3, 4, 5, 6]으로 만들어준다.
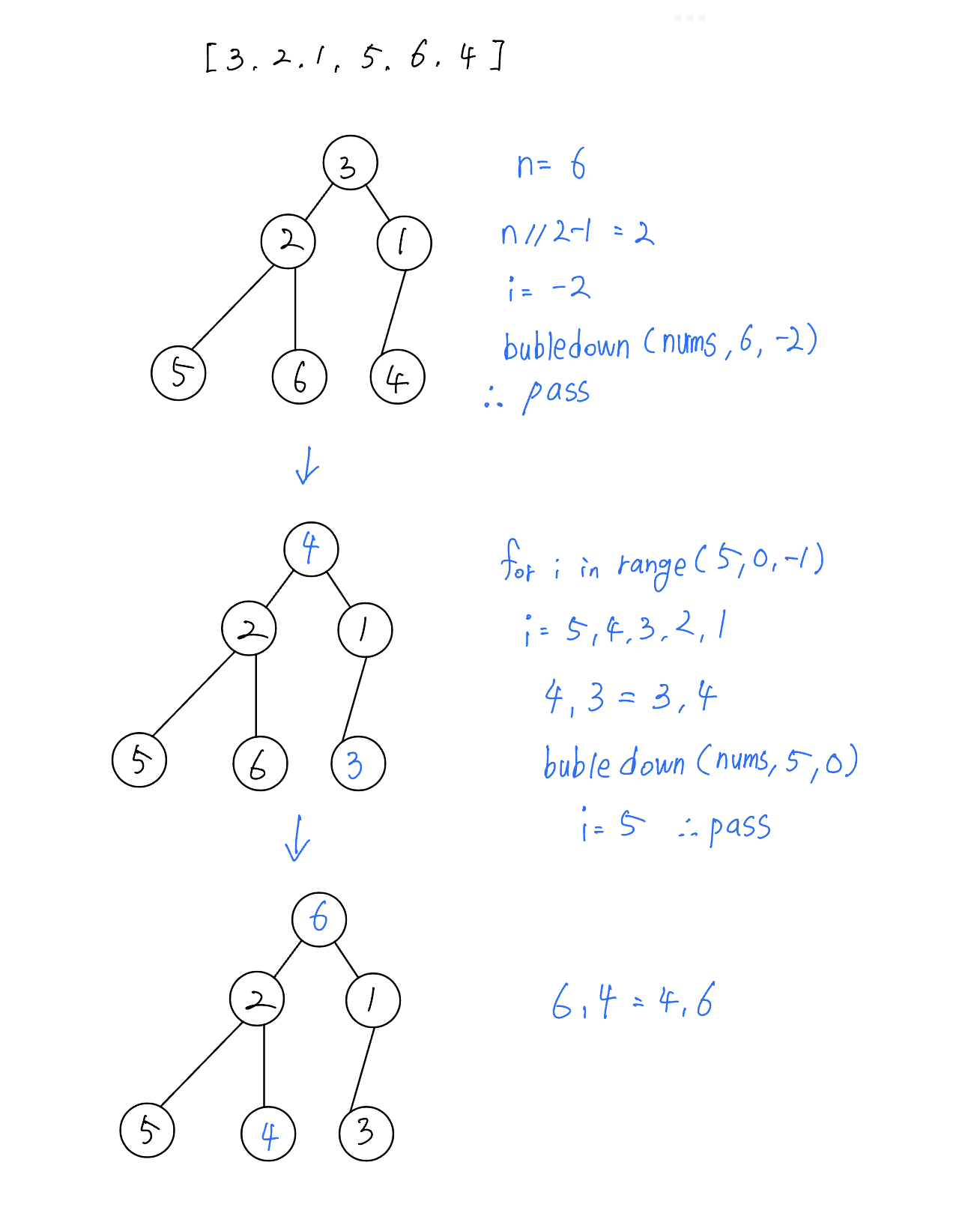
-
Heapify 방법으로 구성하려 했지만 구현하다보니 뭔가 많이 복잡해진 것 같다.
-
과정이 생각대로 이루어지지 않은 것 같은데 일단 모든 테스트 케이스를 통과해서 최종 값은 원하는 값을 반환했지만 굉장히 많은 재귀반복 탓에 성능적으로는 매우 안좋고, 코드 흐름도 따라가기 힘든 것 같다.
-
다른 솔루션을 참고하여 다시 최소 Heap을 활용하여 코드를 구현해보았다.
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
# heapipy 연산을 자동으로 해주는 heap 모듈
import heapq
if not nums:
return 0
heap = []
for i in nums:
heapq.heappush(heap, i)
if len(heap) > k:
heapq.heappop(heap)
return heapq.heappop(heap)Runtime: 2043ms ---> 569ms
Memory: 29.6MB ---> 29.4MB
-
솔루션을 참고해보니 heapq라는 모듈을 알게되었다. heapq 모듈은 최소 Heap 자료구조를 제공하는 파이썬 내장 모듈이었다.
-
heapq를 활용하니 원하는 흐름대로 구현할 수 있었고 수정된 코드는 다음과 같이 동작한다.
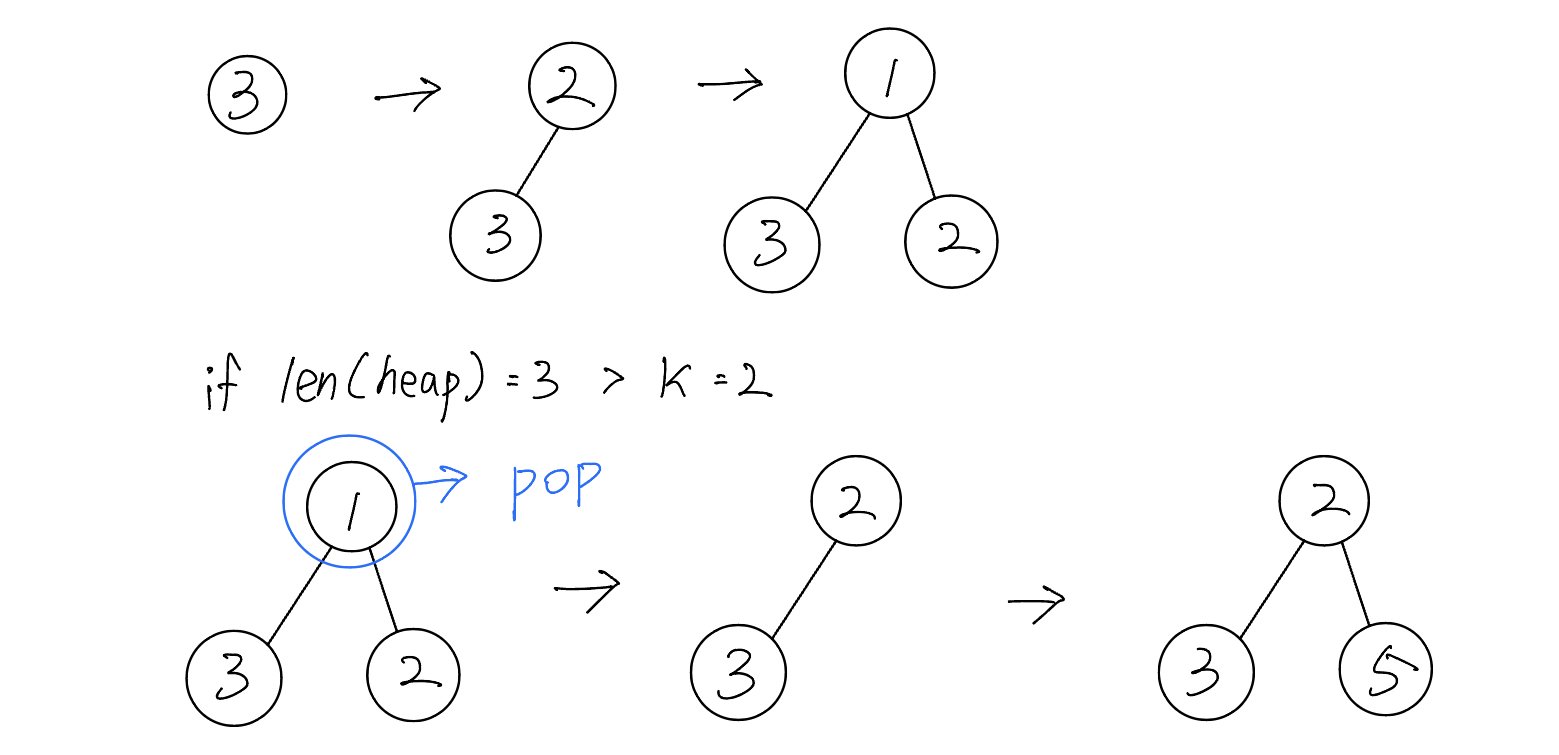
-
heap에 push하면 자동으로 최소 Heap 트리를 구성해주고, push하는 값에 따라 heap이 정렬된다.
-
만약 k보다 heap에 push한 수가 많아지면 root 노드를 pop하고 다시 heap을 구성한다.
-
이렇게 반복되면 k번째 큰 수가 가장 root 노드에 오게 되고, 그 값을 pop한 것을 반환한다.
Runtime은 무려 1/4가량 개선되었다. 기존 코드는 Heapify 과정에서 많이 꼬인 것 같다는 것을 느꼈다.
Heap은 우선순위 큐와 관계가 깊기 때문에 매우 중요한 자료구조라고 생각하며, 앞으로도 Heap을 사용할 때 heapq 모듈도 적극적으로 활용 해봐야겠다.
그리고 하면 할 수록 자료구조가 어렵게 느껴지지만, 그만큼 성능적인 코드구현에는 중요하다는 것을 깨달으며 Heap과 같은 트리구조에 익숙해지도록 여러 문제들을 풀어봐야겠다.
