[코테] 99클럽 코테 스터디 1일차 TIL (BOJ 11657)

문제

https://www.acmicpc.net/problem/11657

풀이

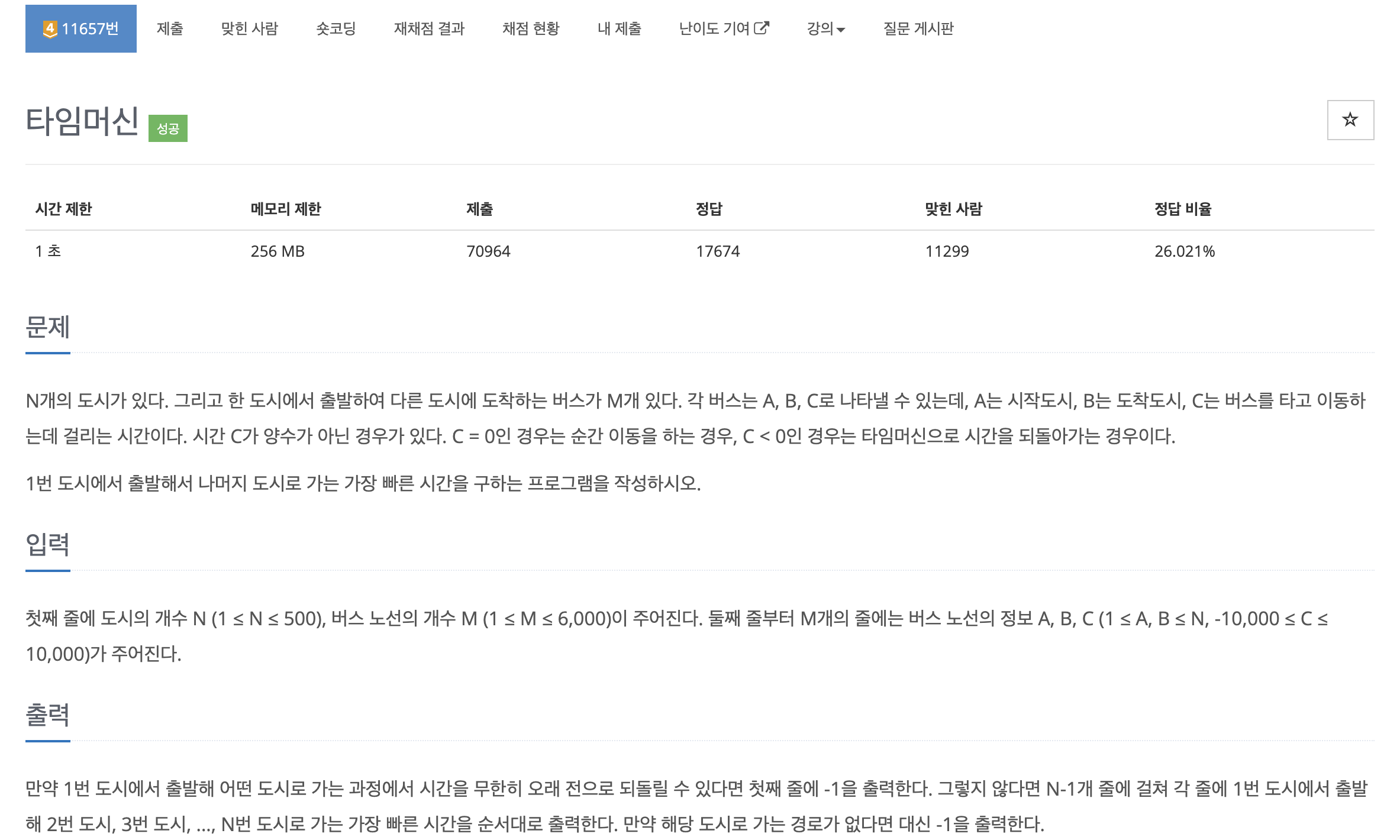
1번 도시에서 출발해 다른 도시로 가는 가장 빠른 시간을 구하는 문제였다.
다익스트라 알고리즘이 먼저 떠올랐으나 음수 간선이 포함되어 있어 대신 벨만-포드 알고리즘을 사용했다.

N-1번 반복 후에도 최단 거리가 갱신되는 간선이 있다면, 음수 사이클이 존재한다고 판단하였다.

import sys

def bellmanford(start):
    distance = [INF] * (n + 1)
    distance[start] = 0

    for i in range(n):
        for now in range(1, n+1):
            for node, node_cost in graph[now]:
                if distance[now] != INF and distance[now] + node_cost < distance[node]:
                    distance[node] = distance[now] + node_cost
                    if i == n-1:
                        return -1

    return distance

INF = sys.maxsize
n, m = map(int, input().split())
graph = [[] for _ in range(n+1)]

for _ in range(m):
    a, b, c = map(int, input().split())
    graph[a].append((b, c))

result = bellmanford(1)

if result == -1:
    print(-1)
else:
    for i in range(2, n+1):
        if result[i] == INF:
            print(-1)
        else:
            print(result[i])

TIL

벨만-포드 알고리즘의 음수 사이클 검출 방식과 다익스트라와의 차이점을 명확히 이해하였다.
다만 다익스트라 알고리즘에 비해 시간이 오래 걸린다는 단점이 있다.