통계_기초

wonder1ng·2024년 3월 28일

통계 기초

빅데이터 교육

목록 보기

1/4

01_통계 기초

01-01_확률

확률: 특정한 사건이나 결과가 발생할 가능성
확률의 종류:
- 주관적 판단-주관적 확률: 경험과 직관에 의한 주관적인 판단
- 객관적 판단-객관적 확률-사전적 평가-고전적 확률(사전 확률): 각각의 결과가 나올 확률을 객관적으로 미리 판단 가능한 경우
- 객관적 판단-객관적 확률-사전적 평가-장기적 상대도수 확률(사후 확률): 같은 실험을 수없이 반복했을 때 특정 사건이 발생할 상대적 가능성

01-02_표본과 모집단

실험: 어떤 행위의 결과를 관찰하고 측정하여 그 결과에 대해 구체적인 값을 부여하는 행위
표본점, 단일사상, 단일사건: 한 번의 실험 결과
표본 공간: 실험 결과로 발생할 수 있는 모든 가능한 결과의 집합
모집단: 분석하고자 하는 대상 전체
모수: 모집단 특성을 나타내는 대푯값(전수조사로 도출)
표본: 모집단의 일부로 실제 관측한 대상
자유도(Degree Of Freedom): 표본-1( $n-1$ ).
평균: 모평균 $(\mu)=\frac{1}{N}\sum_{i=1}^Nx_i$ , $\overline{X}$ , 표본평균 $(\overline{X})=\frac{1}{n}\sum_{i=1}^nx_i$
통계량: 표본집단의 특성을 나타내는 대푯값
분산: 데이터의 퍼짐 정도. 모분산 $(\sigma^2)=\frac{1}{N}\sum_{i=1}^N(x_i-\mu)^2$ , 표본분산 $(V　or　S^2)=\frac{1}{n-1}\sum_{i=1}^n(x_i-\overline{X})^2$
표준편차: 각 측정값과 평균의 차이를 측정하여 나타낸 산포도. 모표준편차 $(\sigma)=\sqrt{\sigma^2}$ , 표본표준편차 $(S)=\sqrt{S^2}$
비율: 모비율 $(P)=\frac{k}{N}$ , 표본비율 $(\hat{p})=\frac{k}{n}$
변수(variable): 관찰 대상의 속석을 척도로 측정하여 그 결과를 수치로 기록한 값

01-03_확률 변수

01-03-01_개념

확률변수: 표본 공간 상의 모든 표본점들에 수치를 부여하는 규칙
- 이산확률변수: 변수 값이 명확하고 연속되지 않음. 분포 합산 시 1.
- 연속확률변수: 변수 값이 연속됨. 분포 적분 시 면적이 1.
확률분포: 확률변수가 가질 수 있는 값과 확률을 표현한 것.
확률분포 용어
- 확률질량함수(probability mass function: pmf): 이산확률변수에 대응하는 이산확률밀도함수. ex) 이항분포, 초기하분포, 포아송분포
- 확률밀도함수(probability density function: pdf): $f(x)$ . 연속확률변수에 대응하는 연속확률밀도함수. ex) 카이제곱( $X^2$ )분포, t분포, 정규(Z)분포, F분포
- 누적분포함수(cumulative distribution function: cdf): $F(x)$ . 확률분포함수를 누적한 함수

01-03-02_파이썬 구현(scipy, numpy, pandas)

통계를 가르쳐주신 하정훈 교수님의 블로그 참고

확률변수 다루기

rvs: 랜덤 변량
pdf: 확률밀도함수(Probability Density Function)
cdf: 누적 분포 함수
sf: 생존 함수(1-CDF)
ppf: 퍼센트 포인트 함수(CDF의 역함수)
isf: 역 생존 함수(SF의 역함수)
stats: 반환 평균, 분산, (Fisher’s) 스큐 또는 (Fisher’s) 첨도
moment: 분포의 중심이 아닌 모멘트
scipy

from scipy.stats import norm    # norm: 정규확률분포

print(norm.pdf(1))	# pdf: 확률 분포 함수
print(norm.cdf(1))	# cdf: 누적 확률 분포 함수
print(norm.sf(1))	# sf: 생존함수(1-CDF)
print(norm.cdf(1)+norm.sf(1))
print(norm.ppf(norm.cdf(1)), norm.ppf(0.8413447460685429)); # ppf: 확률 분포의 분위수
print(norm.rvs(size=10))	# 임의 난수 size개 생성
# 결과
0.24197072451914337
0.8413447460685429
0.15865525393145707
1.0
1.0 1.0
[ 0.17937386 -0.56137664  0.04134692  0.40640069  0.54560686 -0.33583934
 -0.33333319 -1.50424958  0.87519049  1.03110364]

연습 문제
1. 정규분포의 누적확률값이 0.75인 x값을 구하시오( $\mu=5, \sigma=3$ ).
2. df(dof)=10인 t분포 값을 50개 생성하시오.
3. $\lambda=0.5$ 인 Exp분포의 $x$ =3인 확률값을 찾으시오.

from scipy.stats import t, norm, expon

print(norm.ppf(0.75, loc=5, scale=3))
print(t.rvs(df=10, size=50))
print(expon.pdf(2, scale=1/0.5))

기술통계(descriptive statistics): 데이터의 특성을 한눈에 파악할 수 있도록 데이터를 정리하고 표현하는 방법

기술통계량: 모집단의 특성을 나타내는 통계량. ex) 중심경향: 평균(mean), 중위수(median), 최빈값(mode) / 산포: 분산(variance), 표준편차(standard deviation), 범위(range), 사분위수(IQR) / 분포의 형태: 왜도(skewness), 첨도(kurtosis)

numpy: 수학 계산 관련 패키지

import numpy as np

x = [1,2,3,4,5,6,7,8,9,10]

len(x) # 데이터의 개수
print('평균 = ', np.mean(x)) # 평균
print('분산 = ', np.var(x)) # 분산
print('표본 분산 = ', np.var(x, ddof=1)) # 표본 분산
print('표준편차 = ', np.std(x)) # 표준 편차
print('표본 표준편차 = ', np.std(x, ddof=1)) # 표본 표준 편차
print('최대값 = ', np.max(x)) # 최대값
print('최소값 = ', np.min(x)) # 최소값
print('중앙값 = ', np.median(x)) # 중앙값
print('1사분위수 = ', np.percentile(x, 25)) # 1사분위 수
print('중앙값 = ', np.percentile(x, 50)) # 2사분위 수 = 중앙값
print('3사분위수 = ', np.percentile(x, 75)) # 3사분위 수
print('배열생성 = ', np.linspace(-5,5,5)) # -5에서 5까지 5개의 값을 가진 배열 생성

pandas: 데이터 관련 패키지

import pandas as pd

x = [1,2,3,4,5,6,7,8,9]
y = [_**2. for _ in x]
x, y = x+[10], y+[None]
df = pd.DataFrame({'x': x, 'y': y})
display(df.describe())
df.info()

# 결과
            x			y
count	10.00000	10.000000
mean	5.50000		38.500000
std		3.02765		34.173577
min		1.00000		1.000000
25%		3.25000		10.750000
50%		5.50000		30.500000
75%		7.75000		60.250000
max		10.00000	100.000000

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10 entries, 0 to 9
Data columns (total 2 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   x       10 non-null     int64  
 1   y       9 non-null      float64
dtypes: float64(1), int64(1)
memory usage: 288.0 bytes

##############################################

df = pd.Series(x)
len(df) # 데이터의 개수
print('평균 = ', df.mean()) # 평균
print('표본 분산 = ', df.var(ddof=0)) # 분산
print('분산 = ', df.var()) # 표본 분산
print('표본 표준편차 = ', df.std(ddof=0)) # 표준 편차
print('표준편차 = ', df.std()) # 표본 표준 편차
print('최대값 = ', df.max()) # 최대값
print('최소값 = ', df.min()) # 최소값
print('중앙값 = ', df.median()) # 중앙값
print('1사분위수 = ', df.quantile(0.25)) # 1사분위 수
print('중앙값 = ', df.quantile(0.50)) # 2사분위 수 = 중앙값
print('3사분위수 = ', df.quantile(0.75)) # 3사분위 수

01-04_분포

01-04-01_개념

정규분포: 연속확률분포 중 가장 대표적 분포로 종모양.
- 특징:
  1)평균 중심으로 종모양 좌우대칭.
  2)확률밀도함수 곡선과 X축 사이의 전체면적의 합은 1.
  3)확률변수 X가 취할 수 있는 값의 구간에 정규분포 곡선도 존재하는 것으로 가정
- 조건: 1)확률변수 값의 68.26%가 $\mu\pm1\sigma$ 안에, 95.44%가 $\mu\pm2\sigma$ 안에, 99.74%가 $\mu\pm3\sigma$ 안에 있어야 함.
  2) 종모양의 중앙이 볼록할수록 정규분포에 가까워짐.
- 위치모수(location parameter): 평균에 따라 그래프 자체가 좌우로 이동
- 척도모수(scale parameter): 분산에 따라 분포 변양 변화
- 표준정규분포: $\mu$ (평균)=0, $\sigma^2$ (분산)=1인 정규분포
t분포: 평균이 0, 표준편차가 1인 구릉이나 종모양의 좌우대칭 분포. 자유도에 따라 그 모양이 변하고 자유도가 30개 이상이면 표준정규분포와 거의 일치함.
표준분산 이용하여 모평균 추정
- 특징:
1) 평균값 0.
2) 자유도에 따라 분포 모양 변화
3) 자유도가 30미만인 경우 양쪽 끝이 평평하고 두터운 꼬리모양
4) 자유도 증가에 따라 분산 1에 수렴
5) 표본이 30개 이상일 경우 Z분포와 거의 동일
카이제곱분포: 독립적인 확률변수를 각각 제곱힌 후 합한 분포.
모분산 추정에 사용.
- 특징:
1) 항상 양의 값만 가짐
2) 오른쪽 꼬리 형태의 비대칭분포
3) 자유도에 따라 모양 변화
4) 자유도가 커질수록 정규분포에 가까워짐
F분포: 2개의 카이제곱분포하는 확률변수값을 각각의 자유도로 나눈 평균 카이제곲값의 비를 변수값으로 하는 확률변수 분포.
분산의 비율 비교.
- 특징:
1) 확률변수 F는 항상 양의 값만 갖는 연속확률변수
2) 카이제곱분포와 다르게 2개의 자유도
3) 자유도에 따라 분포 모양 변화
4) 오른쪽 꼬리 형태의 비대칭분포
5) 자유도가 커질수록 정규분포에 가까워짐

01-04-02_파이썬 구현

정규분포 그리기

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import erf  #erf: 가우스 오차함수(error function)

mu = 0.0        # 모평군
sigma = 0.5     # 모표준편차

x = np.linspace(-5, 5, 1000)
y = (1 / np.sqrt(2 * np.pi * sigma**2)) * np.exp(-(x-mu)**2 / (2 * sigma**2))
y_cum = 0.5 * (1 + erf((x - mu)/(np.sqrt(2 * sigma**2))))

plt.plot(x, y, label=f'pdf of N({mu:.1f}, {sigma:.1f}$^2$)') # Latex 적용 python이 아닌 matplotlib에서 지원. 별도 라이브러리 존재
plt.plot(x, y_cum, label='cdf of N(%.1f, %.1f$^2$)'%(mu, sigma))
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend(loc='upper left')
plt.show()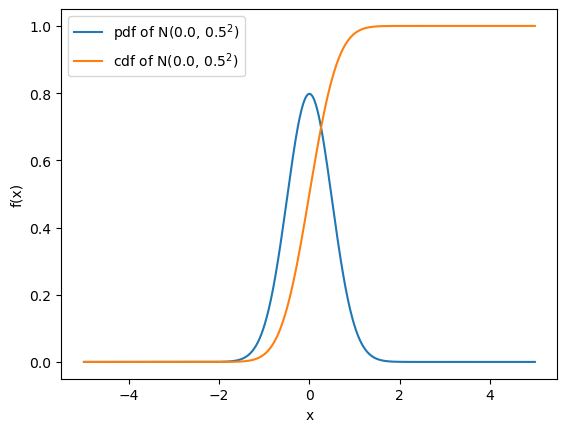

t분포 그리기

import scipy.stats as st

dof = 30
mu = 0.0
sigma = 1.0

x = np.linspace(-5, 5, 1000)

y_normal = st.norm(mu, sigma).pdf(x)
y_t = st.t(dof).pdf(x)

plt.plot(x, y_normal, label='pdf of N(%.1f, %.1f$^2$)'%(mu, sigma))
plt.plot(x, y_t, label='pdf of t(%d)'%dof)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend(loc='upper left')
plt.show()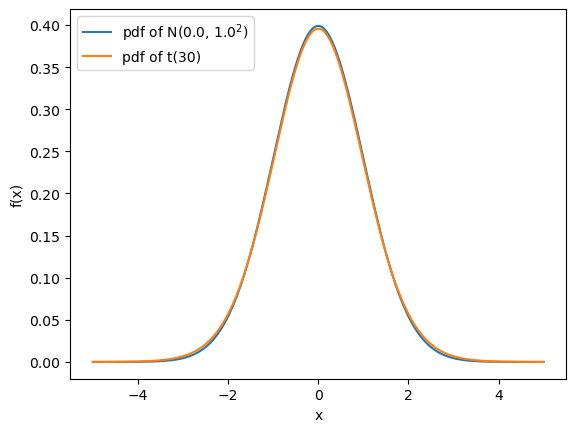

인터렉티브 그래프

import plotly.graph_objs as go
import numpy as np
import pandas as pd
import scipy.stats as stats

dof = 10
mu = 0.0
sigma = 1.0

x = np.linspace(-5, 5, 1000)

y_normal = stats.norm(mu, sigma).pdf(x)
y_t = stats.t(10).pdf(x)

fig = go.Figure()

fig.add_scatter(x=x, y=y_normal, name='pdf of N(%d, %d<sup>2 </sup>)'%(mu, sigma))
fig.add_scatter(x=x, y=y_t, name='pdf of t(%d)'%dof)
fig.show()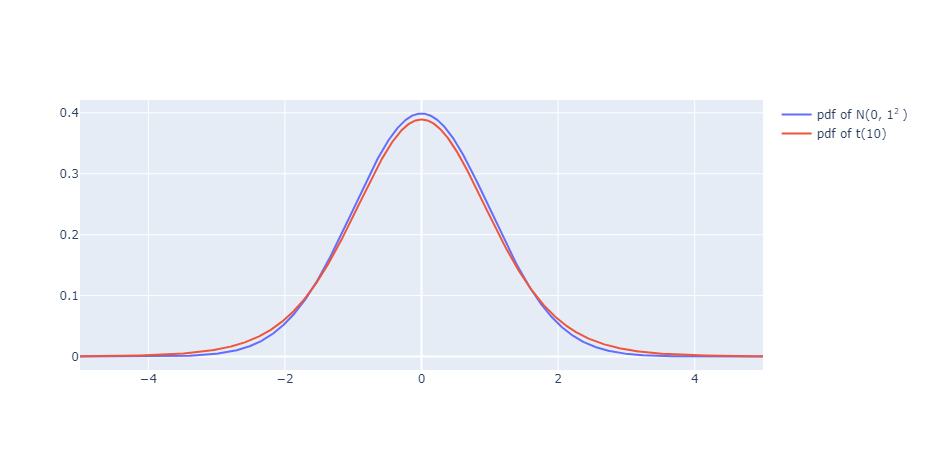

분포 생성하기

import numpy as np
import seaborn as sns

rand_norm = np.random.normal(5,2,100)
print(rand_norm[:5])
print(len(rand_norm))

sns.histplot(rand_norm, bins=np.linspace(0, 10, 10), kde=True);

# 결과
[3.74574333 6.61745706 1.83785367 6.08475513 4.07543715]
100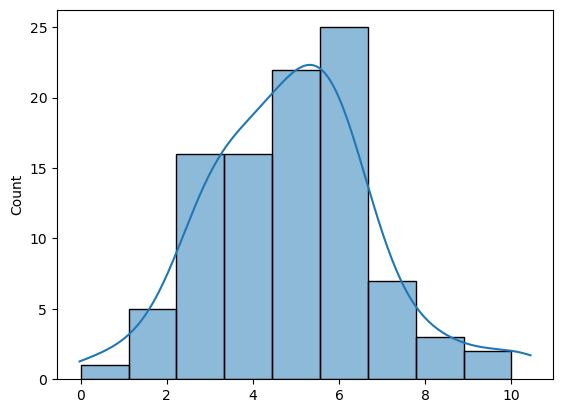

02_중심극한정리와 추정

02-01_중심극한정리

중심극한정리: 표본이 충분히 크면 표본의 값을 모집단의 값처럼 사용할 수 있다.

모집단의 분포와 별개로 추출한 표본크기가 커질수록(30개 이상) 정규분포에 거의 근접하는 분포를 가짐.
평균이 $\mu$ 이고 분산이 $\sigma^2$ 인 임의의 분포를 가진 모집단에서 표본의 크기( $n$ )이 충분히 큰 표본( $n\geq30$ ) 표본평균( $\overline{X}$ )의 분포는 $\overline{X}\sim{N}(\mu, \frac{\sigma^2}{n})$

02-02_추정

02-02-01_개념

추정: 표본을 분석한 통계량으로 모수를 예측하는 일련의 과정
검정: 통계량을 기반으로 통계적 판단을 내리는 것.
통계량(statistic): 표본값을 이용하여 어떤 값을 구하는 수식
추정량(esrimator): 추정을 목적으로 사용하는 특별한 통계량
추정값(estimate): 표본값을 추정량에 대입하여 구한 값
점추정: 추정하고자 하는 모수를 하나의 수치로 추정. ex) 평균, 분산, 표준편차
구간추정: 추정하고자 하는 모수가 존재하리라 예상되는 구간을 정하여 추정.
바람직한 추정량의 조건
- 불편성(Unbiasedness): 추정량의 정확성
- 효율성(Efficiency): 분산이 작을수록 효율적
- 일치성(Consistency): 표본의 크기가 모집단의 크기와 가까운 정도.
- 충족성(Sufficiency): 모수에 대해 정보를 제공하는 정도. 가장 많은 정보 제공할 경우 충족추정량이라 함.
유의수준(significance level, 허용오차수준, $\alpha$ ): 모수( $\delta$ )가 신뢰구간에 포함되지 않을 확률
신뢰계수(confidence coefficient): 1- $\alpha$
신뢰수준(confidence level): 신뢰계수의 백분율
신뢰한계(confidence limits)
- 하한 $\hat\delta_L$ : 추정량의 cdf가 $\frac{\alpha}{2}$
- 상한 $\hat\delta_H$ : 추정량의 cdf가 $1-\frac{\alpha}{2}$
신뢰구간(confidence interval)[ $\hat\delta_L, \hat\delta_U$ ]
- 유의수준이 작을수록 신뢰구간은 커짐
표본평균( $\overline{X}$ )의 분산: $\frac{S^2}{n}\approx\frac{\sigma^2}{n}$
- 유의수준이 작을수록 신뢰구간은 커짐
표본평균( $\overline{X}$ )의 표준편차인 표준오차: $\frac{S^2}{\sqrt{n}}\approx\frac{\sigma^2}{\sqrt{n}}$
표본의 크기( $n$ ): 허용할 수 있는 오차의 크기와 신뢰수준을 고려하여 산정
- $e=\frac{\left(Z(\frac{\alpha}{2})\right)^2S^2}{e^2}$

02-02-02_파이썬 구현

점추정

import numpy as np

# 모집단 생성
from scipy.stats import norm
population1 = np.random.normal(170, 10, 1000)
population2 = norm.rvs(loc=170, scale=10, size=1000)

# 모집단의 평균, 분산, 표준편차
print('모평균 = ', np.mean(population2)) # 평균
print('모분산 = ', np.var(population2)) # 분산
print('모표준편차 = ', np.std(population2)) # 표준 편차

import matplotlib.pyplot as plt
import seaborn as sns
plt.subplot(1,2,1)
sns.histplot(population1, bins=np.linspace(140, 200, 10), kde=True)
plt.subplot(1,2,2)
sns.histplot(population2, bins=np.linspace(140, 200, 10), kde=True)
plt.show()

# 결과
모평균 =  169.775013672695
모분산 =  94.25625021597496
모표준편차 =  9.70856581663713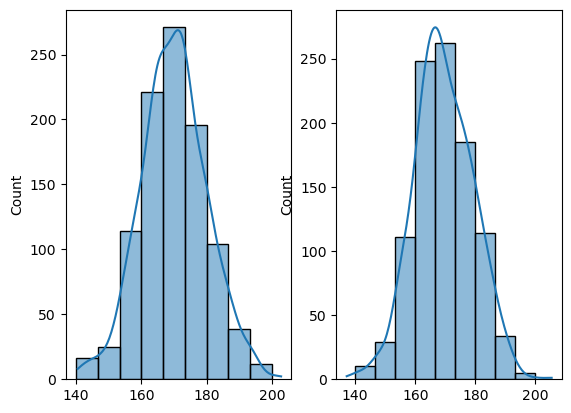

표본 점추정

# 모집단으로 부터 표본의 크기에 따라 샘플링하여 sample에 저장
import random
sample = np.array(random.sample(list(population2),20))

# 표본의 평균, 분산, 표준편차
print('표본평균 = ', np.mean(sample)) # 평균
print('표본분산 = ', np.var(sample, ddof=1)) # 분산, 자유도-1
print('표본표준편차 = ', np.std(sample, ddof=1)) # 표준 편차, 자유도-1

# 결과
표본평균 =  170.15314985143294
표본분산 =  96.92867099409949
표본표준편차 =  9.845235954211534

구간추정

모평균추정(모분산을 모를 경우 $t$ 분포 적용

from scipy.stats import t
import numpy as np, random

sample = np.array(random.sample(list(population2),20))
# 표본크기와 허용오차수준
n = len(sample)
alpha = 0.05

# 1) 표본평균 계산
x_bar = sample.mean()
print('표본평균 = ', x_bar)

# 2) 신뢰수준에 따른 t값계산(t(n-1) 분포의 오른쪽 꼬리의 누적밀도가 alpha/2가 되는 지점)
t_value_low = t.ppf(alpha/2,df=n-1)
t_value_high = t.ppf(1-alpha/2,df=n-1)
print('t값 = ', t_value_low, t_value_high)

# 3) 표준오차(표본평균의 표준편차)
se = np.std(sample, ddof=1)/np.sqrt(n)
print('표준오차 = ', se)

# 4) 신뢰구간 계산
ci_lower = x_bar-t_value_low*se
ci_upper = x_bar+t_value_high*se

print("신뢰구간 = [%.4f, %.4f]"%(ci_lower, ci_upper))

# 결과
표본평균 =  169.9000252659096
t값 =  -2.0930240544082634 2.093024054408263
표준오차 =  1.9289674291023817
신뢰구간 = [173.9374, 173.9374]

# 표본크기와 허용오차수준
n = len(sample)
alpha = 0.05

# 1) 표본평균 계산
x_bar = np.mean(sample)
print('표본평균 = ', x_bar)

# 2) 표준오차(표본평균의 표준편차)
se = np.std(sample, ddof=1)/np.sqrt(n)
print('표준오차 = ', se)

(ci_lower, ci_upper) = t.interval(1-alpha, df=n-1, loc=x_bar, scale=se)

print("신뢰구간 = [%.4f, %.4f]"%(ci_lower, ci_upper))

# 결과표본평균 =  169.9000252659096
표준오차 =  1.9289674291023817
신뢰구간 = [165.8627, 173.9374]

모분산 추정

from scipy.stats import chi2
# 표본크기와 허용오차수준
n = len(sample)
alpha = 0.05

# 1) 표본 표준편차 계산
S = np.std(sample, ddof=1)
print('S = ', S)

# 2) 신뢰수준에 따른 카이제곱값계산
chi2_lvalue = chi2.ppf(1-alpha/2,df=n-1)
chi2_uvalue = chi2.ppf(alpha/2,df=n-1)
print('카이제곱값 = [%.4f, %.4f]'%(chi2_lvalue, chi2_uvalue))

# 3) 신뢰구간 계산
ci_lower = (n-1)*(S**2)/chi2_lvalue
ci_upper = (n-1)*(S**2)/chi2_uvalue

print("신뢰구간 = [%.4f, %.4f]"%(ci_lower, ci_upper))

# 결과
S =  8.626604595711864
카이제곱값 = [32.8523, 8.9065]
신뢰구간 = [43.0395, 158.7543]

예제 보고 풀기

03_가설과 검정

03-01_개념

가설 검정: 모집단 모수에 대한 연구가설의 채택 여부를 모집단으로부터 추출한 표본의 통계량을 이용해서 검정하는 일련의 과정
가설: 두 개 이상의 변수 또는 현상 간의 관계를 검정 가능한 형태로 서술한 것으로 과학적 조사에 의하여 검정이 가능한 사실.
연구가설(대립가설): 연구자가 검정하고자 하는 가설(예상·주장하는 가설)
귀무가설(영가설): 연구자의 가설을 반박하는 가설(기존에 인정되어온 연구자가 반박하고자 하는 가설)
가설 검정 용어
- 유의수준( $\alpha$ ): 귀무가설이 잘못됐다 판단하여 귀무가설을 기각할 확률
- 가설 검정의 3종 오류
  1) 제1종 오류: 귀무가설이 옳은데 기각.
  2) 제2종 오류: 대립가설이 옳은데 기각,
  3) 제3종 오류: 문제 자체를 잘못 정의함. 연구 설계부터 오류.
임계치: 검정의 종류(양측, 단측)와 유의수준( $\alpha$ )을 고려해 산출한 가설 채택 여부를 결정짓는 경계값.
검정통계량( $t$ 값): 표본으로부터 추출한 통계량이나 검정에 사용할 분포에 따라 그에 맞는 값으로 치환한 통계량. $t_x=\frac{\overline{x}-\mu}{S\sqrt{n}}$
$p$ 값( $p$ -value): 표본으로부터 얻은 통계량 혹은 이를 치환한 검정통계량의 절대값보다 더 큰 절대값을 다른 표본으로부터 얻을 수 있는 확률.
두 모집단편균에 대한 표준오차와 t분포 자유도
- 분산이 다른 경우
  - 표준오차: $\sqrt{\frac{S^2_A}{n_A} + \frac{S^2_B}{n_B}}$
  - 자유도: $\frac{\left(\frac{S^2_A}{n_A} + \frac{S^2_B}{n_B}\right)^2}{\frac{\left(\frac{S^2_A}{n_A}\right)^2}{n_A-1} + \frac{\left(\frac{S^2_B}{n_B}\right)^2}{n_B-1}}$
- 분산이 같은 경우
  - 표준오차: $\sqrt{S^2\left(\frac{1}{n_A}+\frac{1}{n_B}\right)}$ ,　　　　　　 $S^2_P=\frac{(n_a-1)S^2_A+(N_B-1)S^2_B}{(nA-1)+(n_B-1)}$
  - 자유도: $n_A+n_B-2$
$F$ 분포의 임계치: 분자 먼저 분모 먼저. $\frac{\sigma^2_A}{\sigma^2_B}<1$ , $1<\frac{\sigma^2_B}{\sigma^2_A}$
검정통계량 F값: $F=\frac{S^2_A}{S^2_B}$

03-02_파이썬

평균차이 검정

scipy 함수
- ttest_1samp(): 단일모집단 평균
- ttest_real(): 단일 모집단 전후 평균 비교
- ttest_ind(): 두개의 모집단 평균 비교
단일표본 t 검정
구현

import numpy as np
from scipy.stats import t

n = 100         # 표본 갯수
mu = 1500       # 모평균(귀무가설)
x_bar = 1420    # 표본평균
S = 200         # 표본오차
akpha = 0.05    # 유의수준

# 임계치 계산
c_val = t.ppf(akpha, df=n-1)
print(f"{c_val = }")

# t 검정통계량 계산
stat = (x_bar-mu)/(S/np.sqrt(n))
print(f"{stat = }")

print(f'H1: mu <  {mu:,}')
print(f'H0: mu >= {mu:,}')
print(f't-stat = {stat:.4f}, critical value = {c_val:.4f}')

if stat > c_val:
    print("Reject_H1")
else:
    print("Accept_H1")
    
# 결과
c_val = -1.6603911559963902
stat = -4.0
H1: mu <  1,500
H0: mu >= 1,500
t-stat = -4.0000, critical value = -1.6604
Accept_H1

예제 및 함수

from scipy import stats
from sklearn.datasets import load_breast_cancer
import numpy as np

# 데이터셋 로딩
data = load_breast_cancer()
# 'mean radius' 특성만 선택
mean_radius = data['data'][:, 0]

# one sample t-test 수행 (귀무가설: mean_radius의 평균은 15)
mu = 15
t_stat, p_value = stats.ttest_1samp(mean_radius, mu)

# 소수점 4자리로 제한하여 출력
print(f"t-statistic: {t_stat:.4f}")
print(f"p-value: {p_value:.4f}")

# p-value 판정
alpha = 0.05  # 신뢰수준 95%
if p_value < alpha:
    print(f"평균이 {mean_radius.mean():.2f}이므로 귀무가설을 기각하므로, mean_radius의 평균은 {mu}가 아닙니다.")
else:
    print(f"평균이 {mean_radius.mean():.2f}이므로 귀무가설을 채택하므로, mean_radius의 평균은 {mu}일 가능성이 높습니다.")

쌍체 비교

from scipy import stats
import numpy as np

# 가상의 무게 데이터 (식용 전, 식용 후)
x_before = np.array([82, 54, 74, 75, 71, 76, 70, 62, 77, 75, 72, 83, 78, 74, 68, 76, 75, 75, 75, 71])
x_after = np.array([75, 50, 74, 71, 69, 73, 68, 62, 68, 72, 70, 77, 71, 74, 67, 73, 77, 71, 76, 74])
x_d = x_before-x_after

n = len(x_d)    # 표본 갯수
mu = 0 # 모평균
x_bar = x_d.mean() # 표본 평균
S = x_d.std(ddof=1) # 표본 오차
print(f'{x_bar = }, {S = }')

# 임계치 계산
alpha = 0.05    # 유의 수준
c_val = t.ppf(akpha, df=n-1)
print(f"{c_val = }")

# t 검정통계량 계산
stat = (x_bar-mu)/(S/np.sqrt(n))
print(f"{stat = }")

print(f'H1: mu <  {mu:,}')
print(f'H0: mu >= {mu:,}')
print(f't-stat = {stat:.4f}, critical value = {c_val:.4f}')

if stat <= c_val:
    print("Reject_H1")
else:
    print("Accept_H1")
    
#### 함수 사용
# # t 검정통계량 계산
# t_stat, p_value = stats.ttest_rel(x_before, x_after)
# # 소수점 4자리로 제한하여 출력
# print(f"t-statistic: {t_stat:.4f}")
# print(f"p-value: {p_value:.4f}")

# print(f't-statistic = {stat:.4f}, p-value = {p_value:.4f}')

# if p_value > alpha:
#     print("Reject_H1")
# else:
#     print("Accept_H1")

두 모집단 평균 비교

from scipy.stats import t
import numpy as np

alpha = 0.05 #유의수준
n_a = 30  #표본 갯수
x_bar_a = 48500 #표본평균 
S_a = 3600  #표본오차
n_b = 30  #표본 갯수
x_bar_b = 52000 #표본평균 
S_b = 4200  #표본오차

# 합동 표준오차 계산
var_ab = np.sqrt(S_a**2/n_a + S_b**2/n_b)

# 자유도 계산
dof_ab = (S_a**2/n_a + S_b**2/n_b)**2/((S_a**2/n_a)**2/(n_a-1) + (S_b**2/n_b)**2/(n_b-1))
print(f'{dof_ab = }')

# t 검정통계량 계산 
stat = (x_bar_a-x_bar_b)/var_ab
print(f'{stat = }')

# 임계치 계산 alpha=0.05 
c_val_low = t.ppf(alpha/2,dof_ab)
c_val_high = t.ppf(1-alpha/2,dof_ab)
print(f'{c_val_low = }, {c_val_high = }')

print('H1: mu_a != mu_b')
print('H0: mu_a = mu_b')
print(f'{stat = :.4f}', f'{c_val_low = :.4f}, {c_val_high = :.4f}')

if (stat <= c_val_low) or (stat >= c_val_high):
	print('Accept H1')    
else:
	print('Reject H1')
    
#### 힘수 사용
# from scipy.stats import ttest_ind

# a = np.random.normal(x_bar_a, S_a, n_a)
# b = np.random.normal(x_bar_b, S_b, n_b)

# stat, p = ttest_ind(a, b)

# print('H1: mu_before > mu_after')
# print('H0: mu_before <= mu_after')
# print('t-stat = %.4f, p = %.4f' % (stat, p))
# if p > 0.05:
# 	print('Reject H1')
# else:
# 	print('Accept H1')

분산차이검정(카이제곱검정)

from scipy.stats import chi2

alpha = 0.05 #유의수준
n = 30  #표본 갯수
sigma_squared = 1.2 #모분산(귀무가설)
S_squared = 1.7 #표본분산 

# Xai2 검정통계량 계산 
stat = (n-1)*S_squared/sigma_squared 

# 임계치 계산 
c_val_l = chi2.ppf(alpha/2,df=n-1)
c_val_u = chi2.ppf(1-alpha/2,df=n-1)

print(f'H1: sigma2_a != {sigma_squared}')
print(f'H0: sigma2_a = {sigma_squared}')
print(f'chi2-stat = {stat:.4f}, critical value = ({c_val_l:.4f}, {c_val_u:.4f})')

# 양측검정
if (stat <= c_val_l) or (c_val_u <= stat):
	print('Accept H1')
else:
	print('Reject H1')

두 모집단분산검정(F-test)

from scipy.stats import f

alpha = 0.05 #유의수준
n_a = 16  #표본 갯수
#x_bar_a = 78.3 #표본 평균
S2_a = 37.5 #표본분산 
n_b = 21  #표본 갯수
#x_bar_b = 76.7 #표본 평균
S2_b = 98.6 #표본분산 

# F 검정통계량 계산 
stat = S2_a/S2_b 

# 임계치 계산 
c_val = f.ppf(alpha,n_a-1,n_b-1)

print('H1: sigma2_a/sigma2_b < 1')
print('H0: sigma2_a/sigma2_b = 1')
print('F-stat = %.4f, critical value = %.4f' % (stat, c_val))

if stat >= c_val:
	print('Reject H1')
else:
	print('Accept H1')

04_분산분석

04-01_개념

분산분석: 3개 이상의 집단 간 평균을 검정하는 분석
- 단일변량 분산분석: 종속변수 1개
  - 일원 분산분석: 독립변수 1개
  - 다원 분산분석: 독립변수 2개 이상
    - 주효과분석: 모든 집단에 1개씩 관측치. 각각의 독립변수가 종속변수에 미치는 영향 분석.
    - 주효과와 상호작용효과분석: 2개 이상의 관측치. 주효과분석 + 2개의 독립변수가 동시에 종속변수에 미치는 영향 분석.
- 다변량 분산분석: 종속변수 2개 이상
일원분산분석 수식
- 편차 수식
  $(y_{ij}-\overline{y}) = (\overline{y}_j-\overline{y}) + (y_{ij}-\overline{y}_j)$
  총 편차　= 집단간 편차+집단내 편차
- 제곱합 수식
  $\sum^{g}_{j}\sum^{n_i}_{i}(y_{ij}-\overline{y})^2 = \sum^{g}_{j}\sum^{n_i}_{i}(\overline{y}_j-\overline{y})^2 + \sum^{g}_{j}\sum^{n_i}_{i}(y_{ij}-\overline{y}_j)^2$
  총 제곱합(SST) 　　= 집단간 제곱합(SSB) + 집단내 제곱힙(SSW)
- 자유도 수식
  $n-1 　　　　= 　　　(g-1)　　　 +　　　 (n-g)$
  총제곱합의 자유도 = 집단간 제곱합의 자유도 + 집단내 제곱합의 자유도
- 분산 수식
  $\frac{\sum^{g}_{j}\sum^{n_i}_{i}(y_{ij}-\overline{y})^2}{n-1} =$ 총평균제곱(MST) = 총분산
  $\frac{\sum^{g}_{j}\sum^{n_i}_{i}(\overline{y}_j-\overline{y})^2}{g-1} =$ 집단간 평균제곱(MSB) = 집단간 분산
  $\frac{\sum^{g}_{j}\sum^{n_i}_{i}(y_{ij}-\overline{y}_j)^2}{n-g} =$ 집단내 평균제곱(MSW) = 집단내 분산
- 검정통계량 F값 수식
  $\frac{MSB}{MSW}$
이원분산분석 주효과 수식
- 편차 수식
  $(y_{ij}-\overline{y}_{··}) = (\overline{y}_{i·}-\overline{y}_{··}) + (\overline{y}_{·j}-\overline{y}_{··}) + (\overline{y}_{··}-\overline{y}_{i·}-\overline{y}_{·j}+y_{ij})$
  총 편차 = 요인 i에 의한 편차(요인 i의 주효과) + 요인 j에 대한 편차(요인 j의 주효과) + 요인 i와 j에 의하여 설명할 수 없는 편차(오차)
- 제곱합 수식
  $\sum^{c}_{i=1}\sum^{g}_{j=1}(y_{ij}-\overline{y}_{··})^2 = \sum^{c}_{i=1}\sum^{g}_{j}(\overline{y}_{i·}-\overline{y})^2 + \sum^{c}_{i}\sum^{g}_{j=1}(\overline{y}_{·j}-\overline{y}_{··})^2 + \sum^{c}_{i=1}\sum^{g}_{j=1}(\overline{y}_{··}-\overline{y}_{i·}-\overline{y}_{·j}+y_{ij})^2$
  총 제곱합(SST) = 요인 i에 의한 제곱합(SSB $_i$ ) + 요인 j에 의한 제곱합(SSB $_j$ ) + 오차제곱합(SSE)
- 자유도 수식
  $cg-1 = (c-1) + (g-1) + (c-1)(g-1)$
  총제곱합의 자유도 = 요인 i에 의한 집단간 제곱합의 자유도 + 요인 j에 의한 집단간 제곱합의 자유도 + 요인 i와 요인 j에 의한 집단간 제곱합의 자유도
- 분산 수식
  -
- 검정통계량 F값 수식
  요인 i $= \frac{MSB_i}{MSE}$ , 요인 j $= \frac{MSB_j}{MSE}$
이원분산분석 주효과와 상호작용효과 수식
- 편차 수식
  $(y_{ijk}-\overline{y}_{··}) = (\overline{y}_{i·}-\overline{y}_{··}) + (\overline{y}_{·j}-\overline{y}_{··}) + (\overline{y}_{··}-\overline{y}_{i·}-\overline{y}_{·j}+y_{ij}) + (y_{ijk}-\overline{y}_{ij})$
  총 편차 = 요인 i에 의한 편차(요인 i의 주효과) + 요인 j에 대한 편차(요인 j의 주효과) + 요인 i와 j의 상호작용에 의한 편차(상호작용효과) + 요인 i와 요인 j에 의해 설명되지 않는 집단내 편차(오차)
- 제곱합 수식
  $\sum^{c}_{i=1}\sum^{g}_{j=1}\sum^{h_ij}_{k=1}(y_{ijk}-\overline{y}_{··})^2 = \sum^{c}_{i}\sum^{g}_{j}\sum^{h_ij}_{k=1}(\overline{y}_{i·}-\overline{y})^2 + \sum^{c}_{i}\sum^{g}_{j}\sum^{h_ij}_{k=1}(\overline{y}_{·j}-\overline{y}_{··})^2 + \sum^{c}_{i}\sum^{g}_{j}\sum^{h_ij}_{k=1}(\overline{y}_{··}-\overline{y}_{i·}-\overline{y}_{·j}+y_{ij})^2 + \sum^{c}_{i}\sum^{g}_{j}\sum^{h_ij}_{k=1}(y_{ijk}-\overline{y}_{ij})^2$
  총 제곱합(SST) = 요인 i에 의한 제곱합(SSB $_i$ ) + 요인 j에 의한 제곱합(SSB $_j$ ) + 요인 i와 j에 의한 제곱합(SSB $_{ij}$ ) + 오차제곱합(SSE)
  - c: 요인 i에 의해 구분되는 집단의 수(i첨자로 구분)
  - g: 요인 j에 의해 구분되는 집단의 수(j첨자로 구분)
  - $h_{ij}$ : 요인 i와 요인 j에 의해 구분되는 집단 내 관측치의 수(k첨자로 구분)
- 자유도 수식
  $\sum^{c}_{i}\sum^{g}_{j}h_{ij}-1 = (c-1) + (g-1) + (c-1)(g-1) + \sum^{c}_{i}\sum^{g}_{j}(h_{ij}-1)$
  총제곱합의 자유도 = 요인 i에 의한 집단간 제곱합의 자유도 + 요인 j에 의한 집단간 제곱합의 자유도 + 요인 i와 요인 j에 의한 집단간 제곱합의 자유도 + 오차 제곱합의 자유도
- 분산 수식
  -
- 검정통계량 F값 수식
  요인 i $= \frac{MSB_i}{MSE}$ , 요인 j $= \frac{MSB_j}{MSE}$ , 요인 i와 요인 j의 상호작용 $= \frac{MSB_{ij}}{MSE}$

04-02_파이썬

일원분산분석

import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt
import seaborn as sns
import warnings

warnings.filterwarnings("ignore") # hide warnings
major = ['ma', 'ar', 'en','ma', 'ar', 'ma', 'ar', 'en', 'ma', 'en', 'ma', 'en']
soju = [2.5, 0.5, 2.0, 3.0, 2.0, 2.0, 1.0, 1.0, 1.0, 0.5, 3.0, 1.5]

df = pd.DataFrame({'major': major, 'soju': soju})    
print(df[df.major=='ar'])
print(df[df.major=='en'])
print(df[df.major=='ma'])
# the "C" indicates categorical data
formula = 'soju ~ C(major)'
model = ols(formula, df).fit()

print(model.summary())

print(sm.stats.anova_lm(model))

이원분산분석(주효과)

# 불러올 파일의 경로를 filename 변수에 저장
filename = '../data/data_2_2.csv'
# pandas read_csv로 불러오기
df = pd.read_csv(filename)
print(df)

# data 변환
df = df.melt(id_vars=['volumn'],var_name='location', value_name='sales')
print(df)

# the "C" indicates categorical data
formula = 'sales ~ C(volumn) + C(location)'
model = ols(formula, df).fit()

#print(model.summary())

print(sm.stats.anova_lm(model))

이원분산분석(주+상호작용 효과)

# 불러올 파일의 경로를 filename 변수에 저장
filename = '../data/data_2_3.csv'
# pandas read_csv로 불러오기
df = pd.read_csv(filename)
print(df)

# the "C" indicates categorical data
formula = 'sales ~ C(volumn)*C(location)'
model = ols(formula, df).fit()

print(sm.stats.anova_lm(model))

# interaction plot
from statsmodels.graphics.factorplots import interaction_plot
fig = interaction_plot(df.volumn, df.location, model.fittedvalues, 
            colors=['red','blue'], markers=['D','^'], ms=10)
import matplotlib.pyplot as plt
plt.show()

# Pooling
formula_p = 'sales ~ C(volumn) + C(location)'
model_p = ols(formula_p, df).fit()

print(sm.stats.anova_lm(model_p))

# interaction plot
from statsmodels.graphics.factorplots import interaction_plot
fig = interaction_plot(df.volumn, df.location, model_p.fittedvalues, 
            colors=['red','blue'], markers=['D','^'], ms=10)
import matplotlib.pyplot as plt
plt.show()

정규성 검정(Shapiro Test)

print('\n*****   Normality Test   *********************************************')
df.boxplot('strength', by='temp')
s,p = shapiro(a1); print('A1: stat = %.4f, p-value = %.4f' %(s, p))
s,p = shapiro(a2); print('A2: stat = %.4f, p-value = %.4f' %(s, p))
s,p = shapiro(a3); print('A3: stat = %.4f, p-value = %.4f' %(s, p))
s,p = shapiro(a4); print('A4: stat = %.4f, p-value = %.4f' %(s, p))
print('************************************************************************')

등분산 검정(Bartlett, Levene Test)

print('\n*****   Equal Variance Test   ****************************************')
s,p = bartlett(a1, a2, a3, a4) 
print('Bartlett: stat = %.4f, p = %.4f' %(s, p))
s,p = levene(a1, a2, a3, a4) 
print('Levene:   stat = %.4f, p = %.4f' %(s, p))
print('************************************************************************')

잔차플롯(Residual Plots)

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import seaborn as sns

#define figure size
fig = plt.figure(figsize=(10,10))
#produce regression plots
resid = np.array(model.resid)
fitted = np.array(model.fittedvalues)

# Q-Q Plot
ax1 = plt.subplot(221)
stats.probplot(resid, dist=stats.norm, sparams=(0,1), plot=plt)
plt.xlabel("Residuals")
plt.title("Normal Q-Q Plot")

# Residual Plot
ax1 = plt.subplot(222)
plt.scatter(fitted, resid)
plt.hlines(0,np.min(fitted),np.max(fitted),color="red")
plt.xlabel("Fitted values")
plt.ylabel("Residuals")
plt.title('Residual plot')

# Histogram
ax1 = plt.subplot(223)
sns.histplot(resid,bins=10)
#plt.hist(resid,bins=10,rwidth=0.8)
plt.title("Histogram of Residuals")

# Scale-Location plot
ax1 = plt.subplot(224)
model_norm_residuals_abs_sqrt = np.sqrt(np.abs(resid))
sns.regplot(x=fitted, y=model_norm_residuals_abs_sqrt,
              scatter=True,
              lowess=True,
              line_kws={'color': 'red', 'lw': 1, 'alpha': 0.8})
plt.ylabel("Standarized residuals")
plt.xlabel("Fitted value")
plt.title("Scale-Location plot")

사후분석 다중비교(FWER: Familywise Error Rate): 여러 개의 가설 검정을 할 때 적어도 하나의 가설에서 1종 오류가 발생할 가능성

from statsmodels.sandbox.stats.multicomp import MultiComparison
import scipy.stats

comp = MultiComparison(df.strength, df.temp)

# Bonferroni Correction
result = comp.allpairtest(scipy.stats.ttest_ind, method='bonf')
print(result[0])

# Tuckey's Honestly Significant Difference = "진정으로 유의미한 차이"
from statsmodels.stats.multicomp import pairwise_tukeyhsd

hsd = pairwise_tukeyhsd(df['strength'], df['temp'], alpha=0.05)
print(hsd.summary())

05_상관분석과 회귀분석

05-01_상관분석

05-01-01_개념

상관분석: 변수 간의 상관 관계를 파악하는 분석법
- 교차분석: 명목 및 서열 척도
- 스피어만 상관분석: 서열 척도
- 피어슨 상관분석: (제3변수 통제하지 않은) 등간 및 비율 척도
- 편상관분석: (제3변수 통제한) 등간 및 비율 척도
공분산: $\sigma_{xy}=\frac{ \sum_{i=1}^{N}(x_i-\mu_x)(y_i-\mu_y)}{N}$ , $S_{xy}=\frac{ \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{n-1}$
상관계수: 변수 간의 선형적인 관계 정도와 방향을 정량화 하여 표시하는 지수로 표준화된 공분산. $p=\frac{\sigma_{xy}}{\sigma_x\sigma_y}$ , $r=\frac{S_{xy}}{S_xS_y}$
공분산: 변수 간의 공통된 분포를 나타내는 분산으로 변수 간의 선형적인 연관성 정도를 나타냄.

상관계수의 평가: 목적과 자료에 따라 기준은 상이하나 일반적 기준은 다음과 같음

상관계수(r)	r값의 해석
0.2 미만	관계가 거의 없음
0.2 이상 0.4 미만	낮은 상관관계
0.4 이상 0.6 미만	비교적 높은 상관관계
0.6 이상 0.8 미만	높은 상관관계
0.8 이상	매우 높은 상관관계

통계모형
- 수학적 모형: 현상이나 문제를 수학적 개념과 언어를 사용하여 묘사한 것.
- 통계 모형: 변수 간 관계를 나타내며 데이터의 불확실성과 변동성을 설명하는 수학적 모형
  - 통계모형 수립 목적
    - 불확실성의 정량화 -> 구간 추정
    - 추론 -> 표본을 이용한 모집단에대한 추정과 검정
    - 가설에 대한 지지도 측정 -> 가설검정
    - 예측 -> 회귀모형
변수의 종류와 기능적 관계
- 독립변수(X): 종속변수에 영향을 미치는 주요 변수
- 종속변수(Y): 독립변수에 의해 변하는 주요 변수
- 교란변수, 외생변수: 주요 변수 외에 독립변수나 종속변수에 영향을 미치는 변수
- 공변량: Y에 영향을 미칠것으로 판단되는 제3의변수(연속형)
- 매개변수(I): 독립 변수가 종속 변수에 영향 미치는데 중간자 역할을 하는 변수. X->I->Y
- 조절변수(M): X->Y에 영향 미쳐 상관 관계를 다르게 하는 변수
- 선행변수: X를 선행하여 X->Y의 크기에 영향을 미치는 변수
- Collider(C): X, Y에 모두 영향주며 C를 통제하면 X->Y가 변하는 변수
- 억제변수: X, Y에 모두 영향 미쳐 X->Y가 없는 것처럼 만드는 변수
- 허위변수: X, Y 모두에 영향을 미쳐 상관관계가 없으나 있는 것처럼 만드는 변수.
편상관계수: 제3의 변수가 미치는 영향을 제거 후, 두 변수 간의 순수한 상관관계를 나타내는 계수. 제3의 통제변수를 Z라 할 때, 두 변수 X와 Y간의 편상관계수는 Z가 X와 Y에 미치는 선형효과를 제거 후 남은 자차 간의 상관계수.
교차분석: 명목(서열)척도로 측정된 두 변수 간의 상호연관성을 알아보기 위한 분석 방법. 빈도 수와 기대 빈도의 차이를 분석하여 변수 간 연관성 검증.

05-01-02_파이썬 구현

상관분석(피어슨)

import numpy as np
import pandas as pd
import scipy.stats as stats
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns

filename = '../data/data_3_1.csv'
df = pd.read_csv(filename)

# 눈금선 포맷
sns.set_theme(color_codes=True)
# 단순 산점도
#sns.scatterplot(x='weight', y='height', data=df)
# 회귀선 포함 산점도 95% 신뢰구간
sns.regplot(x='weight', y='height', data=df)

# Pearson 상관계수 계산 : Pandas
print(df['weight'].corr(df['height'], method='pearson'))
print(df.weight.corr(df.height, method='pearson'))

# Pearson 상관계수 계산 : Scipy
corr, p = stats.pearsonr(df.weight, df.height)

# 상관계수의 유의성 검정
print('H1: rho != 0')
print('H0: rho = 0')
print('r = %.4f, p = %.4f' % (corr, p))
if p > 0.05:
    print('Reject H1')
else:
    print('Accept H1')

상관분석(스피어만)

filename = '../data/data_3_2.csv'
df = pd.read_csv(filename)

# Spearman 상관계수 계산 : Scipy
import scipy.stats as stats
corr, p = stats.spearmanr(df.prefer_ord, df.morality_ord)

# 상관계수의 유의성 검정
print('H1: rho != 0')
print('H0: rho = 0')
print('r = %.4f, p = %.4f' % (corr, p))
if p > 0.05:
    print('Reject H1')
else:
    print('Accept H1')

교차분석

filename = '../data/data_3_3.csv'
df = pd.read_csv(filename, index_col='telecom')

# Chi2 검정 : Scipy
stat, p, dof, expected =  stats.chi2_contingency(observed=df)

print(dof)
print(expected)

print('H1: row and column are dependent')
print('H0: row and column are independent')
print('chi2_stat = %.4f, p = %.4f' % (stat, p))
if p > 0.05:
    print('Reject H1')
else:
    print('Accept H1')

카이제곱을 이용한 교차분석

import pandas as pd
from scipy.stats import chi2_contingency

# 임의의 의료 데이터 (흡연자 및 비흡연자 중에서 폐암 발생 및 미발생 인원)
data = {'흡연 여부': ['흡연', '흡연', '비흡연', '비흡연'],
        '질병 발생': ['발생', '미발생', '발생', '미발생'],
        '빈도': [30, 70, 10, 90]}
df = pd.DataFrame(data)

# 교차표 생성
cross_tab = pd.crosstab(df['흡연 여부'], df['질병 발생'], values=df['빈도'], aggfunc='sum')

print("교차표:")
print(cross_tab)

# 카이제곱 검정
chi2, p_value, dof, expected = chi2_contingency(cross_tab)

print(f"\n카이제곱 통계량: {chi2:.4f}")
print(f"p-value: {p_value:.4f}")

# 오즈비(Odds Ratio) 계산
odds_ratio = (cross_tab.loc['흡연', '발생'] / cross_tab.loc['흡연', '미발생']) / (cross_tab.loc['비흡연', '발생'] / cross_tab.loc['비흡연', '미발생'])
print(f"\n오즈비: {odds_ratio:.4f}")

# 상대위험도(Relative Risk) 계산
relative_risk = (cross_tab.loc['흡연', '발생'] / (cross_tab.loc['흡연', '발생'] + cross_tab.loc['흡연', '미발생'])) / (cross_tab.loc['비흡연', '발생'] / (cross_tab.loc['비흡연', '발생'] + cross_tab.loc['비흡연', '미발생']))
print(f"상대위험도: {relative_risk:.4f}")

# 결론 도출
if p_value < 0.05:
    print("귀무가설을 기각합니다. 흡연 여부와 질병 발생은 독립적이지 않습니다.")
else:
    print("귀무가설을 기각하지 않습니다. 흡연 여부와 질병 발생은 독립적입니다.")

05-02_회귀분석

05-02-01_개념

회귀분석: 독립변수가 종속변수에 미치는 영향력의 크기를 파악하여 독립변수의 특정한 값에 대응하는 종속변수값을 예측(인과관계)하는 선형모형을 산출하는 방법.
- 단순 회귀분석: 독립변수 1개
- 다중 회귀분석: 독립변수 2개 이상
- 단변량 회귀분석: 종속변수 1개
- 다변량 회귀분석: 종속변수 2개
- 일반 회귀분석: 등간·비율 척도만 재
- 더미변수 회귀분석: 명목·서열 척도 포함
- 선형 회귀분석:독립변수와 종속변수의 관계가 선형
- 비선형 회귀분석: 독립변수와 종속변수의 관계가 비선형
회귀분석의 전재 조건: 독립변수 값을 갖는 종속변수값은 정규분포해야 하며 이들의 분산은 동일해야함. 종속변수값은 서로 독립적이어야 함. 독립변수 간에 다중공선성이 존재하지 않아야 함.
다중공선성: 독립변수 간의 상관성 정도.
최소제곱법: 잔차의 제곱합을 최소화하는 선형식을 찾는 방법.
결정계수( $R^2$ ): 추정된 회귀선이 실제값과 평균 사이의 편차를 얼마나 줄여주는가를 나타내는 지수
추정값의 표준오차: 오차 혹은 잔차의 표준편차. 잔차제곱합(SSE->MSE) 사용.
회귀분석의 분산분석표: 회귀식이 통계적으로 유의한가를 평가하는 방법. 검정통계량 F값으로 유의성 검정.

05-02-02_파이썬 구현

단일회귀분석

import numpy as np
import pandas as pd
import scipy.stats as stats
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns

# 데이터 
df = pd.DataFrame(
    {"weight": [72,72,70,43,48,54,51,52,73,45,60,62,64,47,51,74,88,64,56,56], 
     "height": [176,172,182,160,163,165,168,163,182,148,170,166,172,160,163,170,182,174,164,160]}
)

# 계산의 편의를 위해 변수명 변경 
x = df.weight
y = df.height

# 표본평균 계산
x_bar = x.mean()
y_bar = y.mean()
print('x_bar = %.4f, y_bar = %.4f'%(x_bar, y_bar))

# 제곱합 계산
SS_x = np.sum((x-x_bar)**2)
SS_xy =np.sum((x-x_bar)*(y-y_bar))
print('SS_x = %.4f, SS_y = %.4f'%(SS_x, SS_xy))

# 회귀계수 추정
beta1 = SS_xy/SS_x
beta0 = y_bar-beta1*x_bar
print('y_hat = %.4f + %.4f x_i'%(beta0, beta1))

#### 함수 사용
# 회귀모형 설계: 단순 선형회귀 모형
# formula = 'height ~ weight'

# # statmodels로 회귀분석실시
# # OLS = Ordinary Least Squares(일반 최소 제곱법)
# model = sm.OLS.from_formula(formula, data=df)
# result = model.fit()
# print(result.summary())

# # Outlier
# print('Outliers :')
# outtest = result.outlier_test()
# print(outtest[outtest['bonf(p)']<1])

다중회귀분석

filename = '../data/data_3_6.csv'
df = pd.read_csv(filename)

# 회귀모형 설계: 다중선형회귀 모형
#formula = 'HeatFlux ~ East + South + North'
formula = 'HeatFlux ~ South + North'

# statmodels로 회귀분석실시
# OLS = Ordinary Least Squares
model = sm.OLS.from_formula(formula, data=df)
result = model.fit()
print(result.summary())

# Outlier
print('Outliers :')
outtest = result.outlier_test()
print(outtest[outtest['bonf(p)']<1])

데이터, 풀스택

다음 포스트