FloorBoards

문제

정사각형의 방 String[] room 이 있다

각 격자에는 가로 또는 세로로 타일을 놓을수 있으며
같은 방향의 타일은 하나의 타일로 처리가 가능

타일을 놓을수 없는 곳은 # 로 표시가 되어 있다

방의 바닥을 덮는데 필요한 타일의 최소 수를 리턴

room : 1~10개의 요소가 있는 배열, 각 요소는 1~10 길이의 문자열

예시 입력

1)
".....",
".....",
".....",
".....",
"....."

2) 
".......",
".#..##.",
".#.....",
".#####.",
".##..#.",
"....###"

3)
"####",
"####",
"####",
"####"

4)
"...#..",
"##....",
"#.#...",
".#....",
"..#...",
"..#..#"

5)
".#....",
"..#...",
".....#",
"..##..",
"......",
".#..#."

예시 출력

5
7
0
9
9

생각의 변화

dp 저장의 기본컨셉은 다음과 같다

이전 타일정보에 따라 현재 (i, j) 에서 가질수 있는 최소 타일수가 바뀌게 된다

따라서 이전 타일정보를 dp 인덱스로 사용하고, dp 에는 최소 타일수를 저장한다

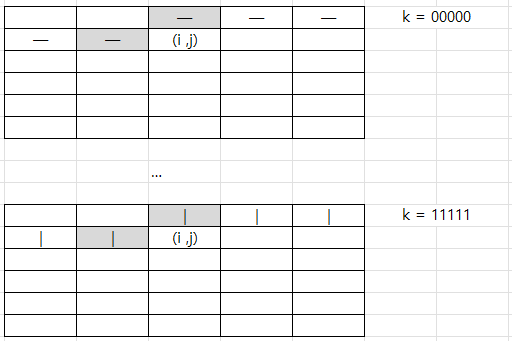
( 타일 하나마다 2개의 상태정보가 존재하므로, 이전 타일정보는 2^가로길이 로 표현된다 )

계산을 간소화 하기위해, dp 인덱스로 이전 타일정보를 표현할때

가로타일과 # 는 0으로 표현하고, 세로타일은 1로 표현한다

(아래에서 별도로 # 채크를 하므로, 둘을 동일하게 두어도 dp 저장결과에 영향을 주지않는다)

(i, j) 에서 가로 막대를 놓을 경우 dp 인덱스는 이렇게 되고

(k << 1) & ((1 << len) - 1)

(i, j) 에서 세로 막대를 놓을 경우 dp 인덱스는 이렇게 된다

horizontal + 1

추가적으로, 막대가 늘어나지 않는 경우는, 2가지 케이스가 존재한다.

1) 위쪽 타일 세로막대 + (i, j) 세로막대인 경우

(k >> (len - 1)) % 2 == 1

2) 왼쪽 타일 가로막대 + (i, j) 가로막대인 경우

k % 2 == 1

위쪽 타일과 왼쪽 타일이 '#' 인지도 체크가 필요하다

room[i-1][j], room[i][j-1

이제, dp[0] = 0 인 상태로 시작해서
room 을 한번 순회하고 나면 dp 에 정보가 채워진다

dp 내에서 최소값을 찾아서 리턴한다

pseudo code

layout(room)
    const int len = room[0].size()
    
    vector<int> dp(1 << len, 99999)
    
    dp[0] = 0
    
    for i=0  i<room.size()  i++
        for j=0  j<len  j++

            vector<int> nextdp(1 << len, 99999)
            
            for k=0  k<(1 << len)  k++
                if dp[k] == 99999
                    continue
                    
                horizontal = (k << 1) & ((1 << len) - 1)
                vertical = horizontal + 1
                
                if (room[i][j] == '#')
                    nextdp[horizontal] = min(nextdp[horizontal], dp[k])
                else
                    if (i != 0 && (room[i - 1][j] != '#') &&
                            (k >> (len - 1)) % 2 == 1)
                        nextdp[vertical] = min(nextdp[vertical], dp[k])
                    else
                        nextdp[vertical] = min(nextdp[vertical], dp[k] + 1)
                        
                    if (j != 0 && (room[i][j - 1] != '#') &&
                            (k % 2 == 0)
                        nextdp[horizontal] = min(nextdp[horizontal], dp[k])
                    else
                        nextdp[horizontal] = min(nextdp[horizontal], dp[k] + 1)
                        
            dp = nextdp
            
    int res = 99999
    
    for (auto d : dp)
        res = min(res, d)
        
    return res