Interesting Party

문제

화이트씨는 친구들을 초대하려고 한다.

친구들은 관심주제 first, second 를 갖고, 둘은 중복되지 않는다.
친구들은 파티주제가 '관심주제' 인 경우에만 초대가 가능하다.

화이트씨가 최대로 초대할수 있는 친구 수를 구한다.

예시 입력

1)
first = {"fishing", "gardening", "swiming", "fishing"}
second = {"hunting", "fishing", "fishing", "biting"}

2)
first = {"variety", "diversity", "loquacity", "courtesy"}
second = {"talking", "speaking", "discussion", "meeting"}

3)
first = {"snakes", "programming", "cobra", "monty"}
second = {"python", "python", "anaconda", "python"}

4)
first = {"t", "o", "p", "c", "o", "d", "e", "r", "s", "i", "n", "g", "l", "e", "r", "o", "u", "n", "d", "m", "a", "t", "c", "h", "f", "o", "u", "r", "n", "i"}
second = {"n", "e", "f", "o", "u", "r", "j", "a", "n", "u", "a", "r", "y", "t", "w", "e", "n", "t", "y", "t", "w", "o", "s", "a", "t", "u", "r", "d", "a", "y"}

예시 출력

4
1
3
6

생각의 변화

first 는 i 고, second 는 j 라는 생각에서 out

루프를 돌릴수 있는 가짓수가 4개

• f[i] 두고 s[j] 를 올려가며 ans 획득
• s[i] 두고 f[j] 를 올려가며 ans 획득

f 나 s 내에서만 나올수도 있으니 (3번 예시)

• f[i] 두고 f[j] 를 올려가며 ans 획득
• s[i] 두고 s[j] 를 올려가며 ans 획득

f[i] 를 두고 f[j] 를 올린것과, f[i] 두고 s[j] 를 올린것은 의미적으로 같은 효과

따라서 ans 를 합친다

pseudo code

bestInvitation(first, second)
    int ans
    
    for  i=0  i<first.size()  i++
        int f = 0
        int s = 0
        
        for  j=0  j<first.size()  j++
            if  first[i]==first[j]
                f++
            if  first[i]==second[j]
                f++
            if  second[i]==first[j]
                s++
            if  second[i]==second[j]
                s++
                
        if  f>s
            ans = max(f, ans)
        else
            ans = max(s, ans)

    return ans

응용 기술

연관배열 (map<string,int>) 을 사용하면 for 문을 1개로 줄일수 있다.

애초에

first[i] 가 first[j], second[j] 를 비교하고
second[i] 가 first[j], second[j] 를 비교하는 구조가 필요한 이유는

(두사람간) 집합관계가 4개 존재하기 때문이다

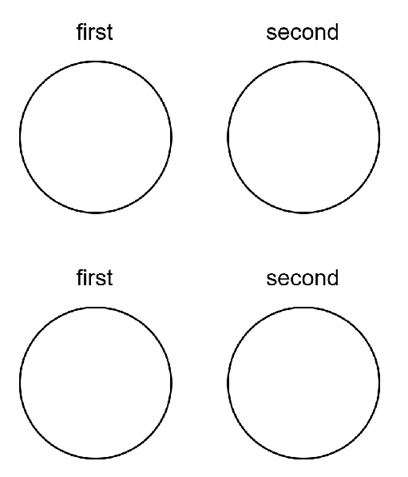
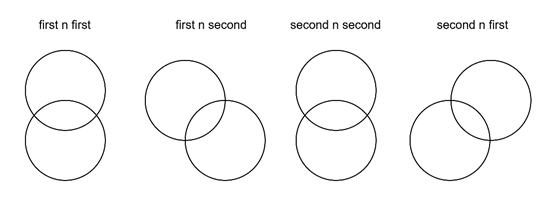
한 사람이 first second 가 같은 경우는 없으므로
key 가 다를 것이라는 걸 알 수 있고

자신이 듣고싶은 얘기를 자기들이 보드에 마킹해두는 식으로
문제를 변경하면 for loop 가 1개로 통일된다.

pseudo code

map<string,int> dict

for  i=0  i<first.size()  i++
    dict[first[i]]++
    dict[second[i]]++