Knapsack

문제

베낭에 최대 10까지의 무게를 담을 수 있고

각 물건의 무게와 가치는 아래와 같다

물건    A    B    C    D    E
무게    3    4    1    2    3
가치    2    3    2    3    6

가치가 최대가 되게 담았을때의 가치를 리턴한다

예시 입력

0 0

예시 출력

14

생각의 변화

깊이우선탐색의 경우

w0 v0
인자로 현재 무게와 현재 가치

무게가 넘으면 리턴은 0

사용한 물건을 기록, 탐색끝나면 복귀

무게가 넘으면 리턴은 v

재귀식에 가치를 더해주는 과정이 들어가있다

value 가 max 인 값을 얻어야 한다

weight 가 초과되는 경우 value 를 그대로 리턴하려면

v 누적을 위해 ret 을 사용하였음

무게가 넘으면 -1 리턴
그러면 max 에서 자연스레 거를 것

pseudo code

struct stuff {
    int weight;
    int value;
};

vector<stuff> s = {
    {3, 2},
    {4, 3},
    {1, 2},
    {2, 3},
    {3, 6}
}

bool in_use[] = { false, false, false, false, false };

knapsack(w, v)
    if w > 10
        return -1
        
    i = 0
    ret = v
    
    for e : in_use
        if e == false
            in_use[i] = true
            ret = max(ret, knapsack(w + s[i].weight, v + s[i].value))
            in_use[i] = false
        
        i++
    
    return ret

응용 기술

메모화 재귀가 가능한 방식으로 탐색하는 방법도 있다

기존엔 현재 weight 와 value 를 전달했지만

현재 탐색길이와 weight 를 전달하는 방식을 사용하면,
별도로 in_use[] 를 기록해두지 않아도 되고, 메모화 재귀가 가능하다

탐색길이로 하면, 중간에 빠진 경우는 고려가 안되는것 아닌가 라는 생각이 들수있다

ex)
3,2 탐색하고
4,3 건너뛰고 1,2 탐색하려는 경우

하지만, 이 또한 knapsack2(n+1, w) 를 사용해 고려되어있다.

knapsack2(0, 0) 시작

knapsack2(0+1, 0+2) 탐색            // 3,2 탐색
knapsack2(0+1+1, 0+2) 탐색          // 4,3 건너뛰고
knapsack2(0+1+1+1, 0+2+2) 탐색      // 1,2 탐색

pseudo code

dp 를 -1 로 초기화 한후 수행하였다

int weight[5] = {3, 4, 1, 2, 3}
int price[5] = {2, 3, 2, 3, 6}
int maxw = 10

int dp[6][11]  // -1

knapsack2(n, w)
    if w > maxw
        return -1
        
    if n >= 5
        return 0
        
    if dp[n][w] >= 0
        return dp[n][w]
        
    ret = knapsack2(n+1, w)
    
    if w + weight[n] <= maxw
        val = knapsack2(n+1, w+weight[n])
        
        if val != -1
            ret = max(ret, val + price[n])
            
    return dp[n][w] = ret

응용기술

dp 를 활용해 계산하는 방법도 있다

총 무게와 몇 번째 물건까지 고려했는지를 dp[i][j] 로 나타내는 것이다

• 무게 : 가로 눈금
• 값 : 최대 가치합계

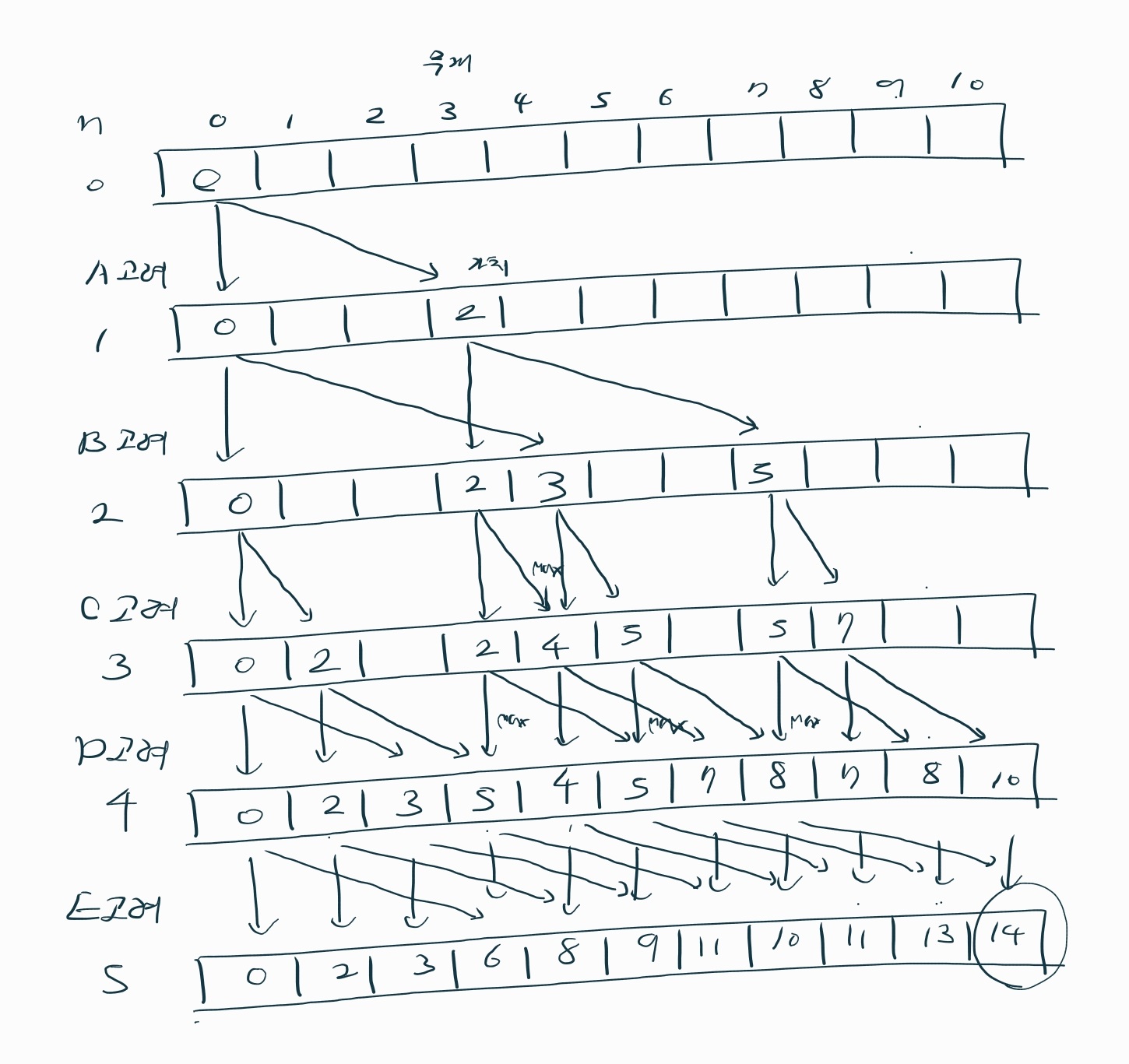
로직을 말로 쓰면 다음과 같다

caveat.
물건을 선택하지 않은 경우를 먼저 반영 (수직 화살표) 하고
이후 물건을 선택한 경우를 반영 (대각선 화살표) 한다

다음 행 값은 다음 행 값과 내 값(dp[i][j]) 중 큰 것

만약 현재 선택한 물건 무게가 눈금 내이면
다음 행 값은 다음 행 값과 내 값에 물건 가치를 더한 것(dp[i][j] + price[i]) 중 큰 것

caveat 에서 설명했듯이
dp의 경우 n[0..5] 로 진행하며 모든 경우를 체크하게 된다
여기에는 중간에 건너뛴 경우도 포함된다

pseudo code

dp 를 0 으로 초기화 한후 수행하였다

int weight[5] = {3, 4, 1, 2, 3};
int price[5] = {2, 3, 2, 3, 6};
int maxw = 10;

int dp[6][11];    // 0

knapsack(n, w)
    for i=0  i<5  i++
        for j=0  j<=maxw  j++
            dp[i+1][j] = max(dp[i+1][j], dp[i][j])
            
            if j+weight[i] <= maxw
                dp[i+1][j+weight[i]] = max(dp[i+1][j+weight[i]], 
                                           dp[i][j]+price[i])
                                           
    ret = 0
    
    for k=0  k<=maxw  k++
        ret = max(ret, dp[5][k]
        
    return ret