레드블랙 트리

레드블랙 트리 작성에 필요한 생각의 변화를 작성하고, 구현을 진행한다.

• 특히 주요 문제상황들과, 생각하기 쉽게 표현하는 방법에 초점을 맞추었다.
• 규칙(현상) 을 만들어내는 생각을 최대한 표현하였다.

기본규칙

1) 모든 node 는 red 나 black 이다.
2) root node 는 black 이다.
3) leaf node 는 black 이다.
4) red 의 자식은 항상 black 이다. (black 의 자식은 red/black 상관없음)
5) root -- leaf 사이의 black 갯수 (black height) 는 어딜 따라가던 동일하다.

규칙을 만든 생각은 다음과 같다.

• 같은 방향(LL, RR) 으로 2번 삽입되면 이진트리 balance 가 무너지므로,
  그걸 방지하기 위해 위 규칙 (rule) 을 부여한다.

구현 난이도를 낮추기 위해 파생규칙 2개가 더 추가된다.

6) 삽입하는 node 의 색은 항상 red 로 한다.

• 따라서 같은 곳에 2번 삽입이 되면 red-red 가 되면서 4번 규칙이 위배된다.

7) "NIL node 의 색은 black" 으로 한다.

• 삽입시 black height 가 변하는걸 방지해준다.
• 따라서 삽입시 P 가 black 이면 보정작업이 필요하지 않다.

삽입시 마주하는 문제

삽입 후의 상태가 '레드블랙 트리' 가 아니게 되면 보정작업이 필요하다.

삽입시 P 가 black 이면 별다른 규칙없이 그냥 삽입하면 된다.

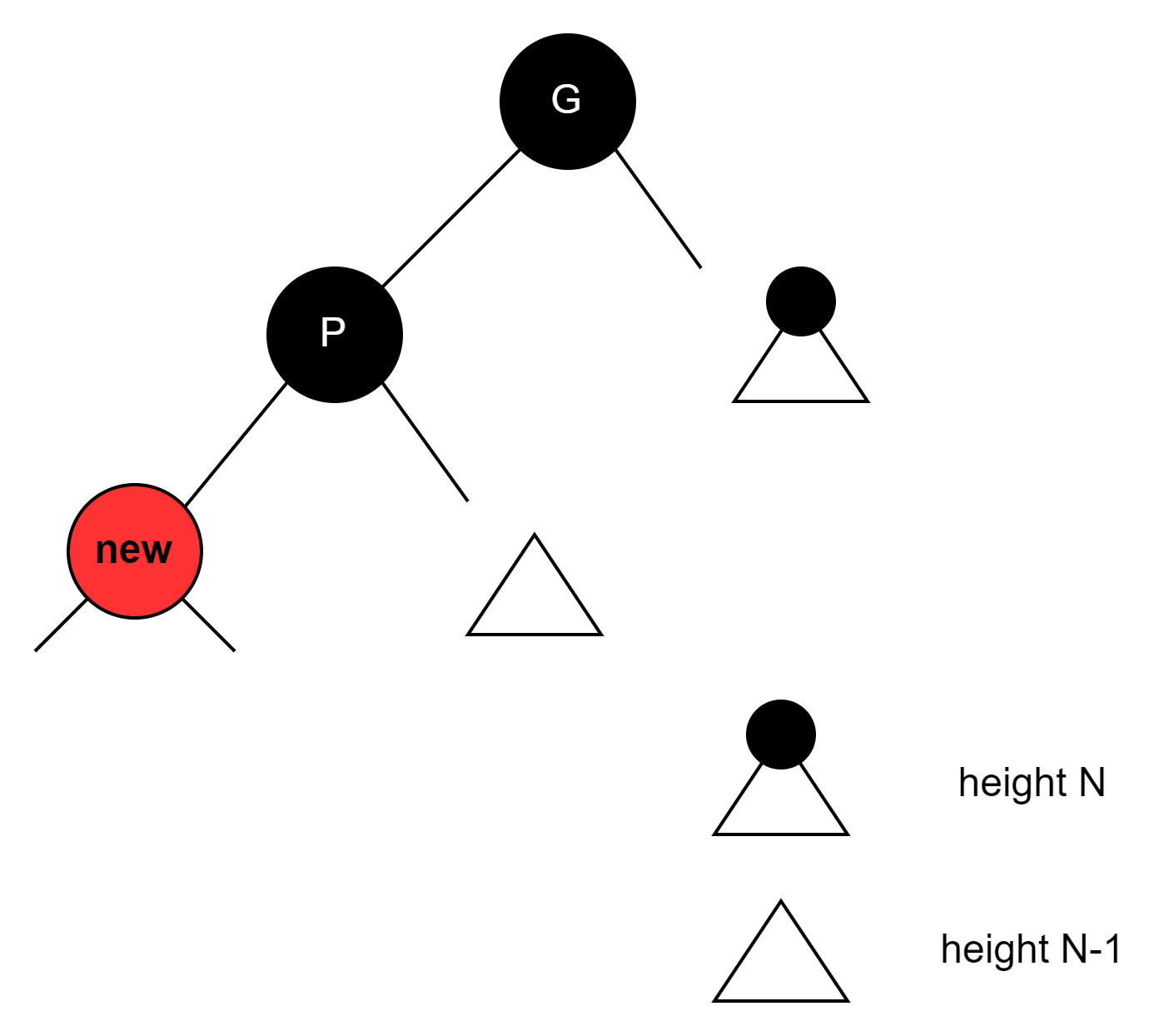
하지만, P 가 red 이면 문제가 있다.

naive 하게 생각하면 new 색깔을 black 으로 바꾸면 될듯 하다.
하지만, 지금 생각하고 있는건 삽입한 leaf node 주변이 아니라, 전체 트리의 상태를
점검하는 것이다. (삽입 후, '전체 트리가 레드블랙 트리' 인지 점검)

따라서 new node 는 처음엔 leaf node 지만, 보정 알고리즘을 돌리면서 트리 중간의
어떤 node 가 될수도 있다.

즉, naive 하게 new 색깔을 black 으로 바꾸면, 이쪽 path 만 black height 가 +1 되어버려, 해야할 일이 더 많아질수 있다.

전체 트리의 상태를 점검할때 고려할 건 2가지이다.
1) red-red 삽입인가
2) black height 가 달라지는가

전체 트리의 상태 관점에서,
red-red 삽입상태를 해소하는 방법은 P U 를 black 으로 바꾸고, G를 red 로 바꾸는 것이다.

( 물론 반대 색깔, 즉 P U 를 red 로 바꾸고, new G 를 black 으로 바꾸는 방법도 가능은 하지만, 이렇게 되면 P U 가 red 이므로 red-red 삽입인지 체크해야 하는 부분이 많아진다. )

그럼 U 가 red 일때랑 black 일때랑 차이점은 없을까? 한번 시도해보자

U 가 red 일때 : 깔끔하다.

U 가 black 일때 : 문제가 된다.

그럼 U 가 black 일때 어떻게 해야 black height 를 맞출수 있을까?
느낌적으로 avl tree 때처럼 회전을 해야 할것 같다. 그럼 n->p 회전이 필요할까 아니면
p->g 회전이 필요할까?

위 그림에서
g 의 right subtree 는 black height 가 n 이고, left subtree 는 black height 가 "n 이상" 이다.

따라서 n->p 회전을 하고서 색을 맞추는건 뭔가 black height 맞추는게 잘 안될것 같으므로,
p->g 회전을 한다.

p->g 회전을 한 후엔 편하게 black height 를 n+1 로 맞추는게 가능함을 볼수 있다.

근데 여기서 드는 생각이 있다.
avl tree 때처럼 p->g 회전을 할때, P의 right subtree 를 G 의 left subtree 로 옮겨주었다.
만약에 new 가 P의 right subtree 면 어떤 일이 일어날까?

이미 P 의 left subtree black height 가 n 으로 작아서, 오른쪽에선 black height 맞추는게
불가능해 보인다.

그럼 어떻게 하면 이 문제를 우회할수 있을까? 사실 문제에 곧 해답이 있다.
new 가 P 의 right subtree 기 때문에 G 의 left subtree 로 넘어간 것이다.

따라서 n->p 회전을 한번해서 아까 잘됬던 상황으로 만들어 준다.

이제 n->g 회전을 해주면 black height 통일이 가능한걸 볼수 있다.

여기까지가 삽입 규칙에 필요한 생각과 표현법들이 되겠다. 아래는 지금까지 설명한 내용들을 정리한 표이다.

삽입 규칙

red N 을 삽입한 후, P G U 에 대해, root 로 올라가는 방향으로 다음 규칙을 적용한다.

(P G 가 R R 일 수 없고, U G 가 R R 일수도 없으므로 표에서 뺐습니다.) 

P G U     행동
-----------------------
B X X     그냥 삽입
R B R     P U 는 BLACK 으로 변경, G 는 RED 로 변경, G 를 new 로 보고 다시 검사
R B B     new 가 outer node 면 p->g 회전, P 는 BLACK, G 는 RED 로 변경
          new 가 inner node 면 n->p 회전 먼저하고, n->g 회전, G 는 RED, new 는 BLACK 으로 변경

R B R 의 경우 root 까지 도달할수 있다. R B R 의 종료조건은 아래와 같다.

(. 는 node 가 없다는 표현)

P G U     행동
-----------------------
R . .    R 을 BLACK 으로 변경
. . .    new 를 BLACK 으로 변경

삭제시 마주하는 문제

삭제는 삽입보다 복잡하므로 red-red violation 문제를 최대한 우회할수 있고, black height 를 보정할수 있는 자연스러운 생각이 필요하다. (전체 케이스를 다 고려하는건 복잡도가 높고, 예외상황을 빼먹을 위험이 다분하다.)

먼저 문제를 단순화 하기위해 이진트리에서 삭제 노드를 보정하는 작업은 이 문제에선 빼둔다.

삭제시 N 이 red 이면 그냥 지우면 된다.

하지만 N 이 black 이면 보정이 필요하다.

먼저 가장 단순한 케이스에서 생각을 시작해본다.

P S C D 가 모두 black 이면, S를 red 로 변경해서 밸런스를 맞출수 있다.
하지만, black height 가 -1 되었으므로, 상위 트리에선 괜찮은지 체크하기 위해 P 를 new N 으로 바꿔서 계속 진행한다.

그럼 S가 red 인 경우엔 어떨까

S 의 색을 바꿔서 삭제된 N 에 대처할수가 없으므로, s->p 회전을 수행해
P 가 black height 를 +1 해주게 한다.

근데, 이렇게 되면 D 쪽이 black height 가 -1 되는 문제가 생긴다. 이를 방지하기 위해
s -- p 끼리 색을 교환한다.

점선친 부분은 P 가 red 인 subtree 이고, 이곳에 대해 분기를 시작할 것이다.

분기 1)
이번에도 가장 단순한 케이스부터 생각해본다

P 가 red 이고 S C D 가 모두 black 이면, s -- p 끼리 색을 교환하고 종료한다.

분기 2)
C 가 red 라면 어떨까

c->s 회전을 하고, 하지만, 이번분기에 나머지까지 다 맞춰지진 않을것 같다.
그래서, c -- s 끼리 색을 교환해서, 분기3 형태로 만들어버린다.

분기 3)
D 가 red 라면 어떨까

s->p 회전을 하고, p/d -- s 끼리 색을 교환해서 C 가 red 이던 black 이던 상관없이
동작할수 있게 안배한다.

여기까지가 삭제 규칙에 필요한 생각과 표현법들이 되겠다. 아래는 지금까지 설명한 내용들을 정리한 표이다.

삭제 규칙(?)

black N 을 삭제한 후, P S C D 에 대해, root 로 올라가는 방향으로 다음 규칙을 적용한다.

P S C D     행동
-----------------------
B B B B     S RED 로 변경, P 는 new 로 보고 다시 검사
B R B B     s->p 회전, s--p 색 교체, p(red) 를 root 로 하는 subtree 에 대해 분기

R B B B     분기1) s--p 색 교체, 종료
R B R B     분기2) c->s 회전, c--s 색 교체, 분기 3으로
R B ? R     분기3) s->p 회전, s--d 색 교체, s 색으로 p 변경, 종료

2번째 규칙에서 다 처리하지 않고, 분기 1~3 으로 현명하게 나누었기에 필요한 생각이 규칙에 잘 녹아들수 있었다.

근데, 한가지 의문점이 남을수 있다.

P S 가 black 이고, C D 중 하나이상이 R 이면 (ex. B B R R) 뭔가 처리해야 하는것 아닐까?

맞는 말이다.

삭제 규칙엔 3가지 경우( B B R R / B B R B / B B B R ) 에 대해 추가가 되어야 한다.

체크해본다.
먼저 B B R R 이다.

다음은 B B B R 이다.

마지막으로 B B R B 이다.

가만보면, D 가 red 일때 ( B B B R / B B R R ) 하는 작업은 위 삭제규칙의 "R B ? R" 과 동일하다. 그리고 C 가 red 일때 ( B B R B ) 하는 작업은 위 삭제규칙의 "R B R B" 와 동일하다.

그럼 지금 알아본 3가지 경우를, 기존 삭제규칙에 포함시킬수 있겠다.

아래는 수정된 삭제규칙이다.

수정된 삭제규칙

black N 을 삭제한 후, P S C D 에 대해, root 로 올라가는 방향으로 다음 규칙을 적용한다.

P S C D     행동
-----------------------
B B B B     S RED 로 변경, P 는 new 로 보고 다시 검사
B R B B     s->p 회전, s--p 색 교체, p(red) 를 root 로 하는 subtree 에 대해 분기

R B B B     분기1) s--p 색 교체, 종료
R/B B R B     분기2) c->s 회전, c--s 색 교체, 분기 3으로
R/B B ? R     분기3) s->p 회전, s--d 색 교체, s 색으로 p 변경, 종료

구현

https://gitlab.com/feather973/data_structure.git

• 커밋 59fc4d82cff9e17e58806dcb40e935fa1da8d588

root@user-virtual-machine:~/data_structure# ./ds -t rbtree3
insert 60
insert 50
insert 100
insert 70
insert 40
insert 80
insert 30
insert 10
insert 20
insert 90
delete 20
[test] remove 20
delete 50
[test] remove 50
delete 80
[test] remove 80
delete 70
[test] remove 70
delete 90
[test] remove 90
delete 40
[test] remove 40
delete 10
[test] remove 10
delete 60
[test] remove 60
delete 30
[test] remove 30
delete 100
[test] remove 100
root@user-virtual-machine:~/data_structure#

구현하면서 새로 알게된 내용

1) node swap 까지 할 필요없이, value 만 swap 하는게 유리하다

• n->val <==> rep->val

2) value swap 후 rep 을 삭제한다.

3) rep 은 자식이 있을 가능성이 있다. 이 경우 rep 을 삭제하지 않고, retry

• n(삭제) -- rep ==> rep(삭제) -- rep 자식 으로 바뀌게 된다.
• rep->val <==> rep자식->val
• value swap 후 rep자식을 삭제

이렇게 하는 이유는 rebalance 는 트리 root 쪽으로 진행하므로, 가급적 leaf node
혹은 leaf node 의 부모를 삭제하는 게, (코드를 깔끔하게 하는데) 유리하기 때문이다.