1 최대공약수, 최소공배수 구하기

---

2 문제

문제 설명
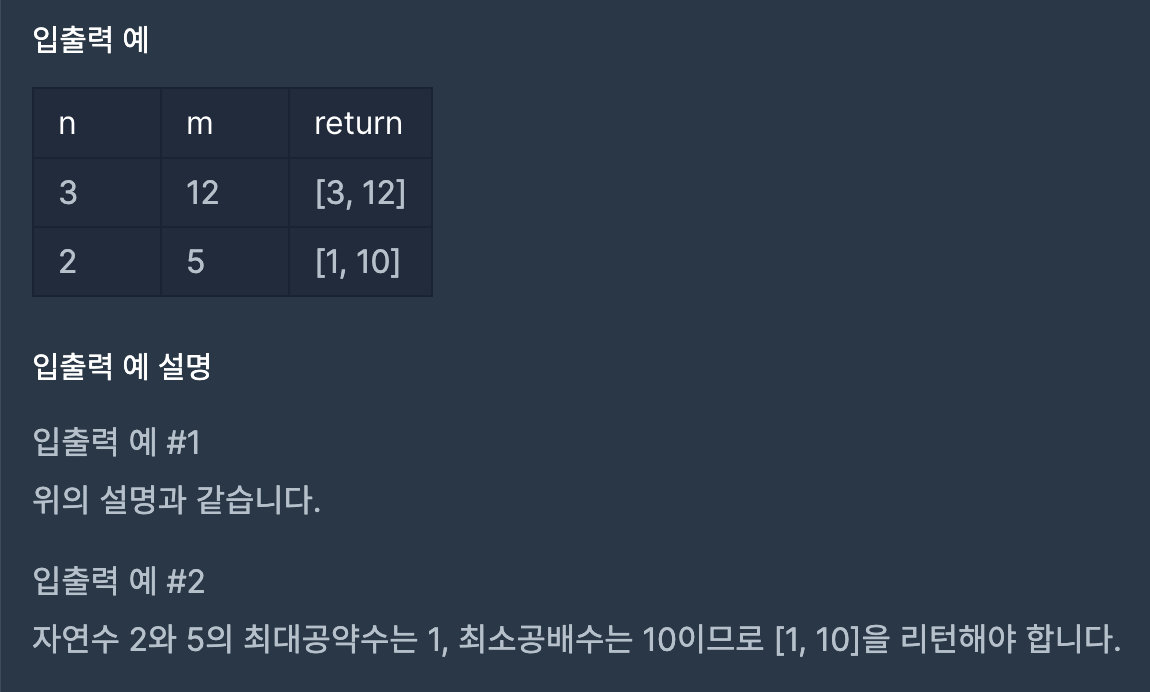
두 수를 입력받아 두 수의 최대공약수와 최소공배수를 반환하는 함수, solution을 완성해 보세요. 배열의 맨 앞에 최대공약수, 그다음 최소공배수를 넣어 반환하면 됩니다. 예를 들어 두 수 3, 12의 최대공약수는 3, 최소공배수는 12이므로 solution(3, 12)는 [3, 12]를 반환해야 합니다.

제한 사항
두 수는 1이상 1000000이하의 자연수입니다.

---

3 풀이

1. 1차 시도

class Solution {
    public int[] solution(int n, int m) {
        int[] answer = new int[2];
         int min = Math.min(n,m);
         int max = Math.max(n,m);
        
        answer[0] = min;
        if(max%min ==0){
            answer[0] = min;
            answer[1] = max;
            
        }else{
            answer[0] = 1;
            answer[1]= min*max;
        }
        
        
        return answer;
    }
}

✏️ 2번째케이스 최대공약수를 통과하지 못했다. 그래서 구글링을 하여
유클리드 호제법을 이용해 최대 공약수를 구할 수 있다는 걸 알게 됐다.

유클리드 호제법

2개 수의 최대 공약수를 구하는 알고리즘이다.

원리는 다음과 같다.

• 자연수 a,b에 대해서 a를 b로 나눈 나머지를 r이라 한다면 a,b의 최대공약수와 b,r의 최대공약수는 같다.

• 이 성질에 따라 a를 b로 나눈 나머지 r을 구하고, b를 r로 나눈 나머지 r'을 구한다.

• 나머지가 0이 될때 나눈 수가 a,b의 최대공약수가 된다.

• 유클리드 호제법으로 최대 공약수를 구한 다음, 최소 공배수는 다음 식에 의해 구할 수 있다.

최소 공배수 : (a ✕ b) / (최대 공약수)

---

2. 유클리드 호제법 이용

class Solution {
    public int[] solution(int n, int m) {
        int[] answer = new int[2];
         int min = Math.min(n,m);
         int max = Math.max(n,m);
         int r = max%min;
        
        if(min%r==0){
            answer[0]=r;
             answer[1]=max*min/answer[0];
        }
        
        return answer;
    }
}

✏️ Exception in thread "main" java.lang.ArithmeticException: / by zero
at Solution.solution(Unknown Source)
at SolutionTest.lambdamain$0(Unknown Source) at SolutionTestSolutionRunner.run(Unknown Source)
at SolutionTest.main(Unknown Source)
테스트 결과 (~˘▾˘)~
2개 중 1개 성공

정수 "0으로 나누기"는 이 클래스의 인스턴스를 발생한다는 의미

---

4 소스 코드

class Solution {
  public int[] solution(int n, int m) {
        int gcd = getGcd(Math.min(n, m), Math.max(n, m));

        return new int[] {gcd, (n * m) / gcd};
    }

    public int getGcd(int min , int max) {
        return max % min != 0 ? getGcd(max % min, min) : min ;
    }
}

• 최대값과 최소값을 구한 뒤 , 유클리드 호제법 원리를 이용한 재귀함수로 문제를 풀었다.

처음에는 쉽다고 생각했는데 생각보다 시간이 걸렸고, 재귀함수를 오랜만에 쓰기에 좋은 예시였다 .