문제 설명 및 링크

프로그래머스 아이템 줍기

문제 설명

다음과 같은 다각형 모양 지형에서 캐릭터가 아이템을 줍기 위해 이동하려 합니다.

지형은 각 변이 x축, y축과 평행한 직사각형이 겹쳐진 형태로 표현하며, 캐릭터는 이 다각형의 둘레(굵은 선)를 따라서 이동합니다.

만약 직사각형을 겹친 후 다음과 같이 중앙에 빈 공간이 생기는 경우, 다각형의 가장 바깥쪽 테두리가 캐릭터의 이동 경로가 됩니다.

단, 서로 다른 두 직사각형의 x축 좌표 또는 y축 좌표가 같은 경우는 없습니다.

즉, 위 그림처럼 서로 다른 두 직사각형이 꼭짓점에서 만나거나, 변이 겹치는 경우 등은 없습니다.

다음 그림과 같이 지형이 2개 이상으로 분리된 경우도 없습니다.

한 직사각형이 다른 직사각형 안에 완전히 포함되는 경우 또한 없습니다.

지형을 나타내는 직사각형이 담긴 2차원 배열 rectangle, 초기 캐릭터의 위치 characterX, characterY, 아이템의 위치 itemX, itemY가 solution 함수의 매개변수로 주어질 때, 캐릭터가 아이템을 줍기 위해 이동해야 하는 가장 짧은 거리를 return 하도록 solution 함수를 완성해주세요.

제한사항

• rectangle의 세로(행) 길이는 1 이상 4 이하입니다.
• rectangle의 원소는 각 직사각형의 [좌측 하단 x, 좌측 하단 y, 우측 상단 x, 우측 상단 y] 좌표 형태입니다.
  • 직사각형을 나타내는 모든 좌표값은 1 이상 50 이하인 자연수입니다.
  • 서로 다른 두 직사각형의 x축 좌표, 혹은 y축 좌표가 같은 경우는 없습니다.
  • 문제에 주어진 조건에 맞는 직사각형만 입력으로 주어집니다.
• charcterX, charcterY는 1 이상 50 이하인 자연수입니다.
  • 지형을 나타내는 다각형 테두리 위의 한 점이 주어집니다.
• itemX, itemY는 1 이상 50 이하인 자연수입니다.
  • 지형을 나타내는 다각형 테두리 위의 한 점이 주어집니다.
• 캐릭터와 아이템의 처음 위치가 같은 경우는 없습니다.

---

• 전체 배점의 50%는 직사각형이 1개인 경우입니다.
  
• 전체 배점의 25%는 직사각형이 2개인 경우입니다.
  
• 전체 배점의 25%는 직사각형이 3개 또는 4개인 경우입니다.
  

---

입출력 예

rectangle	characterX	characterY	itemX	itemY	result
[[1,1,7,4],[3,2,5,5],[4,3,6,9],[2,6,8,8]]	1	3	7	8	17
[[1,1,8,4],[2,2,4,9],[3,6,9,8],[6,3,7,7]]	9	7	6	1	11
[[1,1,5,7]]	1	1	4	7	9
[[2,1,7,5],[6,4,10,10]]	3	1	7	10	15
[[2,2,5,5],[1,3,6,4],[3,1,4,6]]	1	4	6	3	10

입출력 예 설명

입출력 예 #1

캐릭터 위치는 (1, 3)이며, 아이템 위치는 (7, 8)입니다. 위 그림과 같이 굵은 선을 따라 이동하는 경로가 가장 짧습니다.

입출력 예 #2

캐릭터 위치는 (9, 7)이며, 아이템 위치는 (6, 1)입니다. 위 그림과 같이 굵은 선을 따라 이동하는 경로가 가장 짧습니다.

입출력 예 #3

캐릭터 위치는 (1, 1)이며, 아이템 위치는 (4, 7)입니다. 위 그림과 같이 굵은 선을 따라 이동하는 경로가 가장 짧습니다.

입출력 예 #4, #5

설명 생략

접근 방법 및 해결 전략

from collections import deque
import copy


def adjacent_nodes(x, y, field, visited):
    adjacent = []
    for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
        nx, ny = x + dx, y + dy
        if (
            0 <= nx < len(field)
            and 0 <= ny < len(field[0])
            and visited[nx][ny] == 0
            and field[nx][ny] == 1
        ):
            adjacent.append((nx, ny))
    return adjacent


def bfs(characterX, characterY, itemX, itemY, field, visited):
    q = deque()
    q.append([characterX, characterY, 0])
    distance = 0
    visited[characterX][characterY] = 1

    while q:
        x, y, distance = q.popleft()
        if x == itemX and y == itemY:
            return int(distance / 2)

        for i, j in adjacent_nodes(x, y, field, visited):
            if visited[i][j] == 0 and field[i][j] == 1:
                visited[i][j] = 1
                distance += 1
                q.append((i, j, distance))


def solution(rectangle, characterX, characterY, itemX, itemY):
    new_rectangle = []
    for i in rectangle:
        new_rectangle.append(list(map(lambda x: x * 2, i)))

    characterX *= 2
    characterY *= 2
    itemX *= 2
    itemY *= 2

    for x1, y1, x2, y2 in new_rectangle:
        max_x = max(max_x, x1, x2)  # 행
        max_y = max(max_y, y1, y2)  # 열

    # 0,0에서 시작이 아니므로 x,y좌표 1씩 늘려줌
    visited = [[0 for _ in range(max_y + 1)] for _ in range(max_x + 1)]

    # visited를 깊은 복사로 완전 새롭게 복사함
    field = copy.deepcopy(visited)

    # 사각형 외각선 모두 1로 표현
    for i in range(len(new_rectangle)):
        x1 = new_rectangle[i][0]
        y1 = new_rectangle[i][1]
        x2 = new_rectangle[i][2]
        y2 = new_rectangle[i][3]
        for x in range(x1, x2 + 1):
            field[x][y1] = 1
            field[x][y2] = 1
        for y in range(y1, y2 + 1):
            field[x1][y] = 1
            field[x2][y] = 1

    # 사각형 내부에 있는 1을 0으로 바꿈
    for i in range(len(new_rectangle)):
        x1 = new_rectangle[i][0]
        y1 = new_rectangle[i][1]
        x2 = new_rectangle[i][2]
        y2 = new_rectangle[i][3]
        for x in range(x1 + 1, x2):
            for y in range(y1 + 1, y2):
                field[x][y] = 0

    return bfs(characterX, characterY, itemX, itemY, field, visited)

풀이 방법

• solution 함수
  주어진 사각형의 가장 큰 x값과 y값을 이용해 전체 맵의 크기를 field라는 변수로 지정했다. copy라이브러리를 활용해서 visited를 깊은복사했다. 깊은 복사란 값은 같지만 값을 변화했을 때, field와 visited 리스트의 값은 각각 별도로 변화한다.
  이 문제의 아이디어는 rectangle, characterX, characterY, itemX, itemY 값 모두를 2배로 늘리는 것이다. 왜냐하면 아래 그림의 왼쪽을 보면 문제에서는 최단거리가 꺾여서 지나가야하지만 실제로는 오른쪽 그림과 같이 직선으로 이동한다.
  
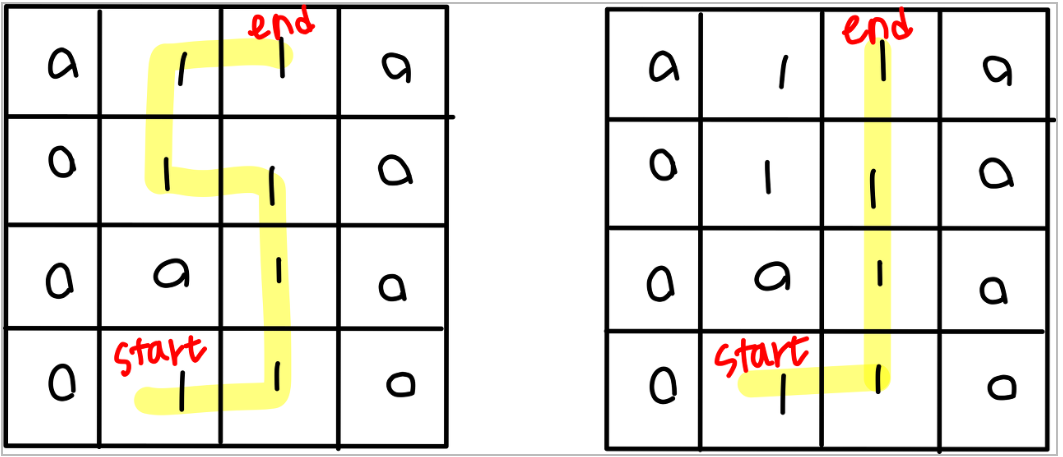
  이러한 경우들 때문에 모든 좌표의 값을 2배로 늘려 오른쪽과 같은 경우가 생기지 않도록 예방했다.

• bfs 함수
  문제에서 원하는 답은 최단거리이기 때문에 BFS를 활용했다. 시작위치에서 양쪽으로 동시에 출발해 거리가 가장 짧은 값을 출력하고자 했다.
  bfs함수를 살펴보면 시작위치는 characterX, characterY로 설정했고 distance는 0이 초기값이다. 그리고 while문으로 들어가 queue의 값을 뽑아내어 itemX, itemY값에 도착했는지 확인한다. 만약 캐릭터가 이동한 위치와 일치하면 int(distance/2)로 값을 답으로 도출한다. 여기서 2로 나눈 이유는 앞에서 우리가 모든 좌표를 2로 늘렸기 때문이다. 그리고 int()를 붙인 이유는 2배늘린 좌표까지의 거리가 홀수인 경우 2로 나누면 소수점이 붙이 때문에 이를 제거하기 위함이다.

• adjacent_nodes 함수
  이 함수는 인접한 노드를 탐색하는 함수이다. 인접한 노드의 좌표를 제한하기 위해서 if문을 작성했다.

1. 0 <= nx < len(field) and 0 <= ny < len(field[0]) and visited[nx][ny] == 0 and field[nx][ny] == 1
2. visited[nx][ny] == 0 and field[nx][ny] == 1 and 0 <= nx < len(field) and 0 <= ny < len(field[0])
   이때, 1번과 2번의 조건은 같아보이지만 순서가 다르다. 2번과 같이 조건을 설정하고 답을 제출하면 에러가 발생한다. 그 이유는 and 연산자는 앞에서부터 조건을 판별하기 때문에 False 조건이 발생하면 그 뒤의 조건을 확인하지 않는다. 그래서 먼저 인접한 좌표가 field를 넘어가지 않았는지 확인하는 조건이 앞에 오는 것이 올바르다.