[백준] 구간 합 구하기 5(11660)

https://www.acmicpc.net/problem/11660

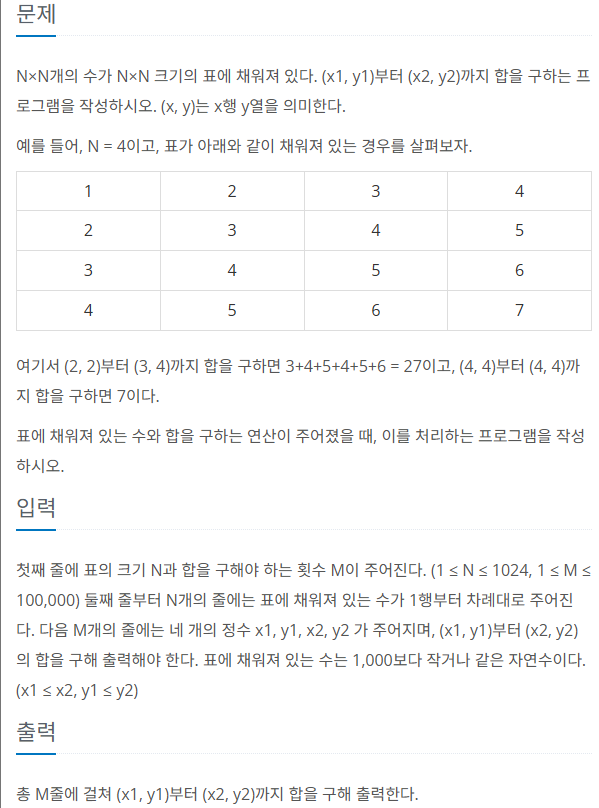
2차원 구간에서 구간 합을 어떻게 구할지가 핵심인 문제이다. 이 역시 각 질의마다 구간합을 구하면 연산량이 늘어나 시간초과가 발생하므로, 미리 구간 합을 구해놔야한다.

2차원 구간에서 합 배열 구하기

$D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]$

여기서 D[i][j-1] + D[i-1][j]를 더하면 이미 D[i-1][j-1]에 해당하는 구간합이 중복해서 2번 더해지므로 D[i-1][j-1]을 빼준다.

그리고 더해야 할 마지막 원소인 A[i][j]를 더하면 된다.

• 더해야 할 마지막 원소?
  1차원 구간에서 A = [1, 2, 3, 4]이라고 생각해보면 구간 합인 S를 구하는 과정에서 마지막 원소는 아래 볼드체와 같다.

  S = [1, 1+2, 1+2+3, 1+2+3+4]

  이 부분을 2차원 구간으로 전환해보면 A[i][j]이다.

글로 보면 헷갈릴 수 있는데, 직접 2차원 좌표를 그려놓고 생각해보면 이해할 수 있을 것이다.

2차원 구간에서 구간 합 구하기

$result = D[x2][y2] - D[x1-1][y2] - D[x2][y1-1] + D[x1-1][y1-1]$

여기서 D[x1-1][y2]와 D[x2][y1-1]를 빼주면 이미 D[x1-1][y1-1]에 해당하는 구간합이 중복해서 2번 빼지므로 D[x1-1][y1-1]을 더해준다.

Python

따라서 파이썬으로 작성한 최종 코드는 아래와 같다.

# 입력 시간을 줄여줄 수 있도록 sys.stdin.readline 사용
import sys
input = sys.stdin.readline

N, M = map(int, input().split())

# 배열에 미리 0을 넣어놓음
# 배열의 인덱스는 1부터 시작
num_arr = [[0] * (N + 1)]
sum_arr = [[0] * (N + 1) for _ in range(N + 1)]

# 원본 배열 입력받기
for i in range(N):
    num_row = [0] + [int(x) for x in input().split()]
    num_arr.append(num_row)

# 합 배열 저장하기
for i in range(1, N + 1):
    for j in range(1, N + 1):
        # sum_arr[i][j-1] + sum_arr[i-1][j]를 연산하면 이미 sum_arr[i-1][j-1]은 2번 더해짐
        # 따라서 sum_arr[i-1][j-1]을 빼준 다음
        # 2차원 배열 대각선 마지막 원소(끝 지점)에 해당하는 원본배열의 num_arr[i][j]를 더함
        sum_arr[i][j] = sum_arr[i][j - 1] + sum_arr[i - 1][j] - sum_arr[i - 1][j - 1] + num_arr[i][j]

for _ in range(M):
    x1, y1, x2, y2 = map(int, input().split())

    # 구간 합을 구할 시작지점인 sum_arr[x1][y1]과 가장 대각선 밑 좌표(끝 지점)인 sum_arr[x2][y2]가 있음
    # 가장 대각선 밑(끝 지점)인 sum_arr[x2][y2]에서
    # y2를 기준으로 행에 해당하는 x1 - 1 좌표 값 만큼 빼줌
    # x2를 기준으로 열에 해당하는 y1 - 1 좌표 값 만큼 빼줌
    # 중복으로 2번 뺄셈이 진행된 x1-1, y1-1 좌표 값을 다시 더함
    result = sum_arr[x2][y2] - sum_arr[x1 - 1][y2] - sum_arr[x2][y1 - 1] + sum_arr[x1 - 1][y1 - 1]
    print(result)

Java

자바로 작성한 문제풀이 코드는 다음과 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class P_11660 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());
        
        // 원본 배열의 크기는 N + 1로 초기화
        int[][] num_arr = new int[N + 1][N + 1];

		// 원본 배열 입력받기
        for (int i = 1; i <= N; i++) {
            st = new StringTokenizer(br.readLine());
            for (int j = 1; j <= N; j++) {
                num_arr[i][j] = Integer.parseInt(st.nextToken());
            }
        }

		// 합 배열의 크기는 N + 1로 초기화
        int[][] sum_arr = new int[N + 1][N + 1];

		// 1 ~ N까지 합 배열 저장하기
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
               sum_arr[i][j] = sum_arr[i][j - 1] + sum_arr[i - 1][j] - sum_arr[i - 1][j - 1] + num_arr[i][j];
            }
        }

		// 구간 요청에 대해 입력받기
        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            int x1 = Integer.parseInt(st.nextToken());
            int y1 = Integer.parseInt(st.nextToken());
            int x2 = Integer.parseInt(st.nextToken());
            int y2 = Integer.parseInt(st.nextToken());
            
            // 요청한 구간 합 출력
            int result = sum_arr[x2][y2] - sum_arr[x1 - 1][y2] - sum_arr[x2][y1 - 1] + sum_arr[x1 - 1][y1- 1];
            System.out.println(result);
        }
    }
}

참고로 파이썬과 자바 코드 모두 배열의 크기를 N + 1로 정하고, 인덱스를 1부터 시작하는 것에 유의하자.

만약 구간 합 (1, 1, 1, 1)을 구하고 싶은 경우 0만큼 빼줄 0번 인덱스가 반드시 필요하기 때문에 일부로 인덱스를 1부터 설정한 것이기 때문이다.