[백준] 수들의 합 5(2018)

https://www.acmicpc.net/problem/2018

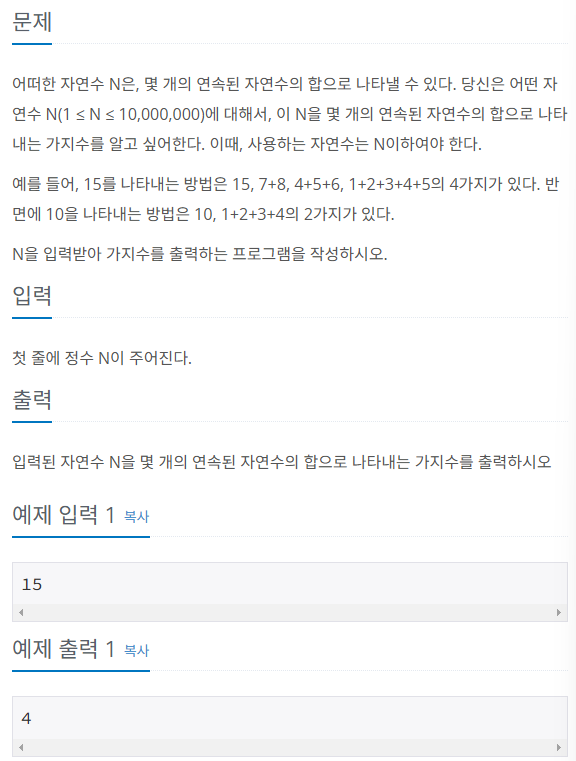
자연수 N의 값이 연속된 자연수의 합으로 표현할 수 있는 개수가 몇 개인지 구하는 문제이다.

N의 범위가 10,000,000으로 매우 큰 수이므로 시간 복잡도가 $O(nlogn)$만 되어도 시간 초과가 발생한다.

따라서 $O(n)$의 시간 복잡도를 가지는 투 포인터 기법을 사용해야 한다.

투 포인터란 start_index, end_index 2개의 포인터를 두고 주어진 문제의 조건에 따라 범위를 유동적으로 조정하는 기법을 말한다.

따라서 문제풀이 방법은 아래와 같다.

1. count를 1로 초기화 => N 자기 자신을 뽑는 경우의 수를 사전에 추가

2. end index가 N과 같아지기 전까지 반복연산

3. 만약 sum == N 이면 정답이다.
   => 정답 count 증가
   => 연속된 자연수의 범위를 한 칸 확장
   (e.g. 1+2 => 1+2+3)
   => 확장한 자연수를 sum에 추가

4. 만약 sum > N 이면
   => sum에서 시작 지점 인덱스의 값을 뺀 후
   => start index의 값을 증가시켜 자연수 범위 한 칸 감소
   (e.g. 1+2+3 => 1+2)

5. 만약 sum < N 이면
   => 연속된 자연수의 범위를 한 칸 확장
   (e.g. 1+2 => 1+2+3)
   => 확장한 자연수를 sum에 추가

Python

N = int(input())
sum = 1
count = 1
start_idx = 1
end_idx = 1

while end_idx != N:
    # 정답인 경우
    if sum == N:
        # 정답 카운트
        count += 1

        # 연속된 자연수의 범위를 한 칸 확장시킴
        end_idx += 1

        # 확장한 자연수를 합계에 추가
        sum += end_idx

    # 연속된 자연수의 합이 입력된 수보다 클 경우
    elif sum > N:
        # 연속된 자연수의 시작지점 인덱스를 합에서 뺀 후
        sum -= start_idx

        # 연속된 자연수에서 왼쪽 값 삭제
        start_idx += 1

    # 연속된 자연수의 합이 입력된 수보다 작을 경우
    else:
        # 연속된 자연수의 범위를 한 칸 확장시킴
        end_idx += 1

        # 확장한 자연수를 합계에 추가
        sum += end_idx

print(count)

뭔가 배열을 사용해야 할 것 같지만 이 경우는 인덱스의 값과 실제로 합계를 구해야하는 값이 동일한 특수한 케이스이다.
e.g. 만약 start index가 4이면 [1, 2, 3, 4, 5]인 배열에서 4에 해당하는 값과 동일

따라서 배열 사용 없이 단순히 sum에 인덱스 값을 더하고 빼는 방식으로 문제를 해결할 수 있다.

Java

자바의 경우도 위 알고리즘을 그대로 사용하면 된다.

import java.util.Scanner;

public class P_2018 {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        long N = sc.nextLong();

        int count = 1;
        int start = 1;
        int end = 1;
        int sum = 1;

        while (end != N) {
            if (sum == N){
                end++;
                sum += end;
                count++;
            }
            else if (sum < N) {
                end++;
                sum += end;
            }
            else if (sum > N) {
                sum -= start;
                start++;
            }
        }

        System.out.println(count);
    }
}