[백준] 이분 그래프(1707)

https://www.acmicpc.net/problem/1707

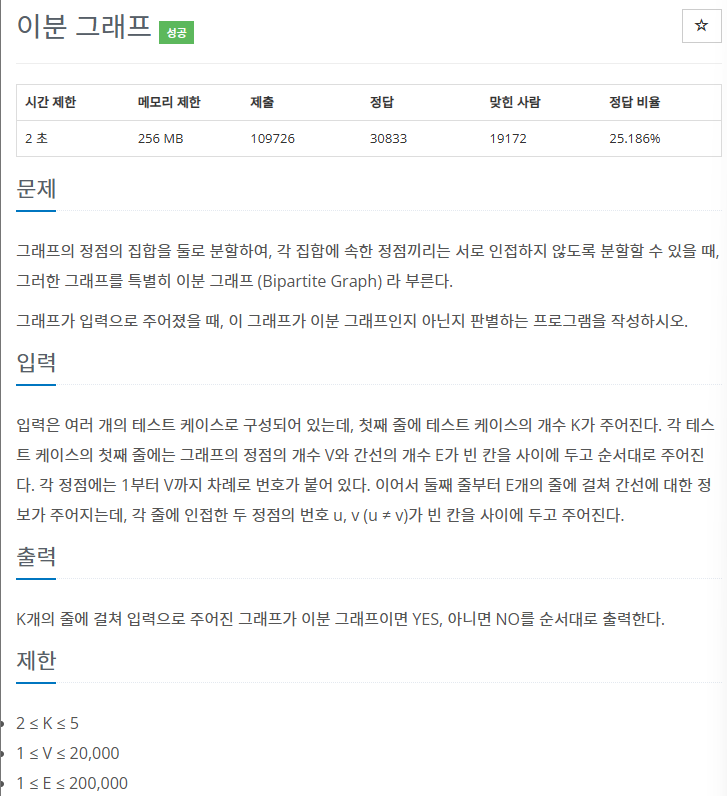
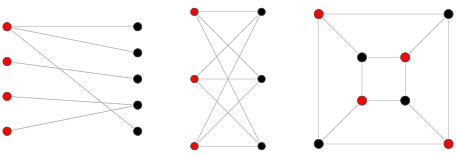
이분 그래프란 인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 2가지 색으로만 표현이 가능한 그래프를 의미한다.

예제의 테스트 케이스를 그림으로 표현해보면 다음과 같다.

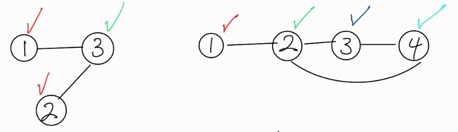
첫 번째 그래프인 1 <-> 2 <-> 3 경우, 모든 정점에 대해 인접한 정점끼리는 서로 다른 색을 칠했을 때 2가지 색으로 표현이 가능하므로 이분 그래프이므로 YES를 출력한다.

두 번째 그래프인 1 <-> 2 <-> 3 <-> 4 <-> 2 경우, 모든 정점에 대해 인접한 정점끼리는 서로 다른 색을 칠했을 때 4가지 색으로 표현할 수 밖에 없으므로 이분 그래프가 아니며, NO를 출력한다.

따라서 이를 판단하기 위해 DFS 탐색을 통해 다음 노드로 이동할 때마다 반대 되는 색을 할당해주면 된다.

다시 말해 각 노드에 대해 탐색하면서 방문하지 않은 노드로 이동할 때마다 0 또는 1로 표현하여 2가지 색깔을 칠해주는 것이다.

따라서 우리는 아래와 같이 check 배열을 노드 개수 크기만큼 선언하여 색깔을 칠해주면 된다.

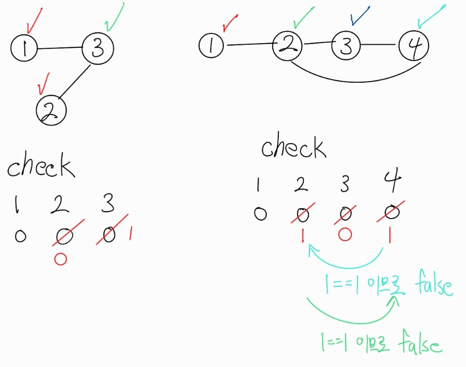
첫 번째 그래프의 경우 1번 노드와 인접한 3번 노드는 check 배열을 0에서 1로 바꿔주고, DFS 탐색을 통해 3번과 인접한 2번 노드는 0에서 0으로 (초기화된 상태와 동일) 바꿔주는 것이다.

마찬가지로 두 번째 그래프의 경우 1번 노드와 인접한 2번 노드는 check 배열에 1로 바꿔주고, 3번 노드는 0, 4번 노드는 1로 바꾼다.

4번 노드에서 2번 노드로 탐색을 진행할 때 서로 같은 색을 가지고 있다면 false로 표시하여 이분 그래프가 아님을 판별한다.

따라서 DFS 소스코드는 다음과 같다.

static void DFS(int v) {
	visited[v] = true;

    for (int i : A[v]) {
    	if (!visited[i]) {
        	check[i] = (check[v] + 1) % 2;
            DFS(i);
		} else if (check[v] == check[i]) {
        	IsBipartite = false;
		}
	}
}

아직 방문하지 않은 노드에 대해서는 check[i] = (check[v] + 1) % 2;를 통해 반대되는 색을 표시해주고, 이미 방문한 노드에 대해서는 서로 같은 색인지 비교하여 이분 그래프를 판별하는 것이다.

따라서 전체 소스코드는 다음과 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;

public class P_1707 {
    static ArrayList<Integer>[] A;
    static boolean[] visited;
    static int[] check;
    static boolean IsBipartite;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int K = Integer.parseInt(br.readLine());

        for (int t = 0; t < K; t++) {
            StringTokenizer st = new StringTokenizer(br.readLine());

            int V = Integer.parseInt(st.nextToken());
            int E = Integer.parseInt(st.nextToken());

            A = new ArrayList[V + 1];
            for (int i = 1; i <= V; i++) {
                A[i] = new ArrayList<>();
            }
            visited = new boolean[V + 1];
            check = new int[V + 1];
            IsBipartite = true;

            for (int i = 0; i < E; i++) {
                st = new StringTokenizer(br.readLine());

                int start = Integer.parseInt(st.nextToken());
                int end = Integer.parseInt(st.nextToken());

                A[start].add(end);
                A[end].add(start);
            }

            for (int i = 1; i <= V; i++) {
                if (IsBipartite)
                    DFS(i);
                else
                    break;
            }

            if (IsBipartite) System.out.println("YES");
            else System.out.println("NO");
        }
    }

    static void DFS(int v) {
        visited[v] = true;

        for (int i : A[v]) {
            if (!visited[i]) {
                check[i] = (check[v] + 1) % 2;
                DFS(i);
            } else if (check[v] == check[i]) {
                IsBipartite = false;
            }
        }
    }
}