[백준] 트리의 지름(1167)

https://www.acmicpc.net/problem/1167

트리에서 두 점 사이의 거리 중 거리가 가장 긴 것을 트리의 지름이라고 하였다.

먼저 트리라는 것은 사이클이 형성되지 않는 연결 그래프를 의미한다.

예제 입력에 대한 그래프 표현은 다음과 같다.

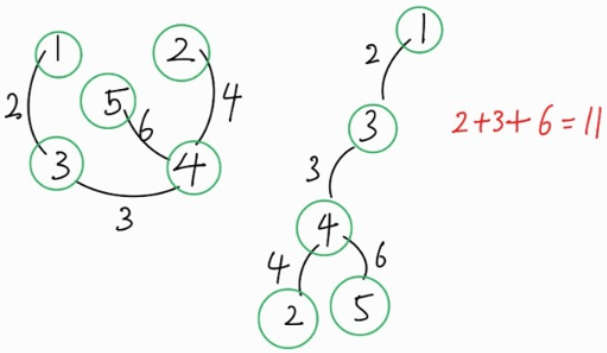
왼쪽 그림은 우리에게 익숙한 그래프 형태로 그린 것이고, 이를 트리 형태로 쫙 펴서 그리면 오른쪽 그림과 같은 형태가 된다.

가장 긴 경로를 구하라고 하였으므로 2 + 3 + 6 = 11 이 결과로 출력되는 것이다.

여기서 핵심은 가장 거리가 긴 경로를 찾기 위해 트리의 양 끝점, 예제에서는 1번, 5번 노드를 찾는 과정을 거쳐야 한다.

결론부터 말하면 이를 해결하기 위해 BFS 탐색을 2번 진행해야한다.

왜냐하면 처음에 임의의 점에서 최장 경로를 기준으로 BFS 탐색을 끝까지 수행하게 되면 트리의 지름에 해당하는 두 노드 중 하나이기 때문이다.

그 이후 임의의 노드에서 시작한 BFS 탐색에서 가장 거리가 먼 노드를 기준으로 다시 BFS 탐색을 진행하게 되면 우리가 구하고자 하는 트리의 지름을 구할 수 있다.

이해를 돕기 위해 아래와 같은 트리가 있다고 가정해보자.

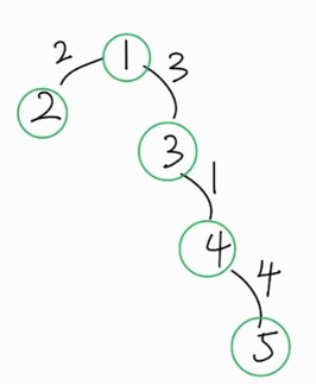
우리가 트리의 지름을 구하기 위해 BFS 탐색 시작 노드가 2라는 것을 알면 정말 좋겠지만, 안타깝게도 어떤 트리 형태가 나올지 모른다.

그래서 임의의 노드, 예를 들어 1을 시작 노드로 하여 BFS 탐색을 진행한다고 가정해보자.

탐색 결과 5까지 도달할 것이고, 간선을 모두 더하면 3 + 1 + 4 = 8이 된다.
여기서 8은 우리가 구하고자 하는 트리의 지름이 아니다. 2번 노드까지 가는 거리인 2가 추가되어야 한다.

따라서 5번 노드를 기준으로 다시 BFS 탐색을 진행하게 되는 것이다.

결과는 4 + 1 + 3 + 2 = 10이 될 것이고, 이는 우리가 구하고자 하는 트리의 지름이 된다.

Python

따라서 문제풀이 코드는 다음과 같다.

import sys
input = sys.stdin.readline
from collections import deque

V = int(input())
A = [[] for _ in range(V + 1)]

for _ in range(V):
    Data = list(map(int, input().split()))
    index = 0
    start = Data[index] # 시작 노드 번호
    index += 1

    while True:
        end = Data[index] # 끝 노드 번호
        # -1인 경우 입력 종료
        if end == -1:
            break
        edge = Data[index + 1] # 시작에서 끝 노드 간의 간선거리
        A[start].append((end, edge)) # (끝 노드, 간선)과 같이 튜플 형태로 추가
        index += 2 # 다음 정보를 받기 위해 인덱스 증가

visited = [False] * (V + 1) # 방문리스트
distance = [0] * (V + 1) # 거리 정보를 저장할 리스트

def BFS(v):
    queue = deque()

    # 탐색을 시작하는 노드를 큐에 push
    visited[v] = True
    queue.append(v)

    # 큐가 비어있을때까지 탐색 진행
    while queue:
        now_Node = queue.popleft() # 현재 노드를 pop

        # 현재 노드를 기준으로 (끝 노드, 간선)을 하나씩 들고옴
        for i in A[now_Node]:
            # 아직 방문하지 않은 노드라면
            if not visited[i[0]]:
                # 큐에 push
                visited[i[0]] = True
                queue.append(i[0])

                # 시작 노드가 가진 간선 정보와 끝 노드가 가진 간선 정보를 더하여 새로운 간선 정보 업데이트
                distance[i[0]] = distance[now_Node] + i[1]

# 임의의 노드에서 탐색 시작
BFS(1)
Max = 1

# 거리가 가장 먼 노드를 찾아내어
# 지름의 끝점을 파악
for i in range(2, V + 1):
    if distance[Max] < distance[i]:
        Max = i

# 거리가 가장 먼 노드를 기준으로 다시 BFS 탐색
visited = [False] * (V + 1)
distance = [0] * (V + 1)
BFS(Max)

# 거리 오름차순 정렬
distance.sort()
# 트리에서 가장 멀리있는 노드 (트리의 지름) 출력
print(distance[V])

입력이 -1인 경우 종료시켜야 하는 구현적인 부분에 대한 스킬이 필요하다.

또한 거리 정보리스트를 새롭게 선언하여 (끝 노드, 간선)과 같이 튜플형태로 저장한 노드에 대한 접근방법도 생각해봐야한다.

distance = [0] * (V + 1) # 거리 정보를 저장할 리스트
...

A[start].append((end, edge)) # (끝 노드, 간선)과 같이 튜플 형태로 추가

마지막으로 시작 노드가 가진 간선 정보와 끝 노드가 가진 간선 정보를 더하여 새롭게 간선 정보를 업데이트 하려는 아이디어가 필요하다.

# 시작 노드가 가진 간선 정보와 끝 노드가 가진 간선 정보를 더하여 새로운 간선 정보 업데이트
distance[i[0]] = distance[now_Node] + i[1]

핵심 알고리즘은 BFS이지만, 이 외에도 여러모로 고려할 부분이 많아서 다소 어려운 문제인거 같다.

Java

따라서 문제풀이 코드는 다음과 같다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class P_1167 {
    static ArrayList<int[]>[] A;
    static boolean[] visited;
    static int[] distance;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int V = Integer.parseInt(br.readLine());

        A = new ArrayList[V + 1];

        for (int i = 1; i <= V; i++) {
            A[i] = new ArrayList<>();
        }

        for (int i = 1; i <= V; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int start = Integer.parseInt(st.nextToken());

            while (true) {
                int end = Integer.parseInt(st.nextToken());
                if (end == -1)
                    break;
                int dist = Integer.parseInt(st.nextToken());
                A[start].add(new int[]{end, dist});
            }
        }

//        // 배열 확인용 출력
//        for (int i = 1; i < A.length; i++) {
//            for (int[] edge : A[i]) {
//                // 배열 내부의 값을 보기 좋게 출력: [정점,거리]
//                System.out.println(Arrays.toString(edge) + " ");
//            }
//            System.out.println();
//        }

        visited = new boolean[V + 1];
        distance = new int[V + 1];
        BFS(1);

        int Max = 1;
        for (int i = 2; i <= V; i++) {
            if (distance[Max] < distance[i])
                Max = i;
        }

        distance = new int[V + 1];
        visited = new boolean[V + 1];
        BFS(Max);

        Arrays.sort(distance);
        System.out.println(distance[V]);
    }

    static void BFS(int v) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(v);
        visited[v] = true;

        while (!queue.isEmpty()) {
            int nowNode = queue.poll();

            for (int[] i : A[nowNode]) {
                int end = i[0];
                int dist = i[1];

                if (!visited[end]) {
                    visited[end] = true;
                    queue.add(end);
                    distance[end] = distance[nowNode] + dist;
                }
            }
        }
    }
}

자바 역시 입력이 -1인 경우 종료하는 구현적인 부분에 대한 스킬과, tuple 대신 int 배열을 사용하여 [정점, 거리] 정보를 담는다.

이후 파이썬과 동일하게 거리 정보 배열도 새롭게 선언하여 최댓값을 찾는 과정이 필요하다.