Linked List with Kotlin

wonseok·2023년 1월 4일

연결리스트(Linked List)는 단방향의 선형 구조의 자료구조이다.
이러한 연결리스트는 코틀린의 Array와 ArrayList에 비해 몇가지 이론적인 장점을 갖는다.

삽입/삭제에 있어서 상수 시간의 시간복잡도를 가진다.
신뢰할 수 있는 성능적인 특성들.

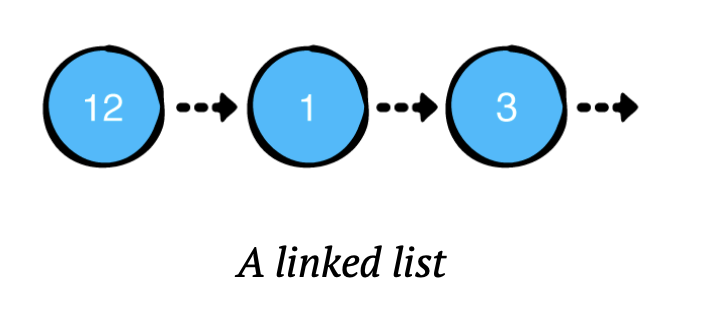
위 그림에서 볼 수 있듯이, 연결리스트는 노드를 줄줄이 이어놓은 것 같다.
여기서 노드는 두 가지 역할을 한다.
1. 값을 가진다.
2. 다음 노드에 대한 참조를 가진다. 다음 노드에 대한 참조가 없다면, null이며, 이것은 연결리스트의 마지막을 의미한다.

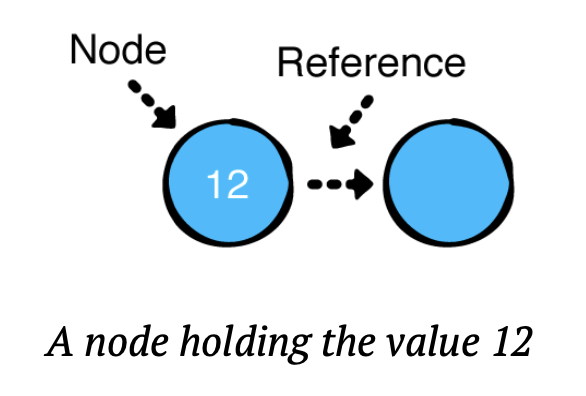
Node

data class Node<T>(var value: T, var next: Node<T>? = null) {
  override fun toString(): String {
    return if (next != null) {
      "$value -> ${next.toString()}"
    } else {
      "$value"
    }
  }
}

우선 Node의 코드는 위와 같이 작성할 수 있다.
이후 main 함수에서 다음과 같은 코드를 작성하면, 아래와 같다.

fun main() {
  "creating and linking nodes" example {
    val node1 = Node(value = 1)
    val node2 = Node(value = 2)
    val node3 = Node(value = 3)
    node1.next = node2
    node2.next = node3
    println(node1)
  }
}

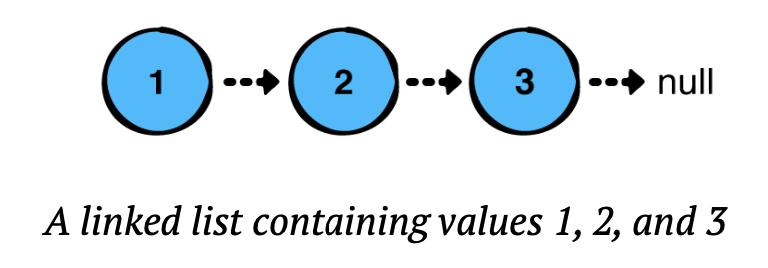
콘솔에 나타난 결과는 아래와 같을 것이다.

1 -> 2 -> 3

LinkedList

class LinkedList<T> {
  private var head: Node<T>? = null
  private var tail: Node<T>? = null
  private var size = 0
  fun isEmpty(): Boolean {
    return size == 0
  }
  override fun toString(): String {
    if (isEmpty()) {
      return "Empty list"
    } else {
      return head.toString()
    }
  }
}

연결리스트는 head와 tail의 개념을 갖는데, 이것은 각각 처음과 끝의 노드를 의미한다.

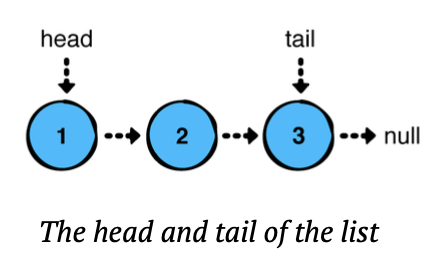
연결리스트에 값을 추가하는 방식에는 push, append, insert 3가지가 있다.
1. push는 연결리스트의 맨 앞에 값을 추가한다.
2. append는 연결리스트의 맨 뒤에 값을 추가한다.
3. insert는 특정 노드 뒤에 값을 추가한다.

해당 포스트에서는 가장 중요한 insert에 대해서만 다뤄볼려고 한다.

insert

fun insert(value: T, afterNode: Node<T>): Node<T> {
  // 1
  if (tail == afterNode) {
    append(value)
    return tail!!
  }
  // 2
  val newNode = Node(value = value, next = afterNode.next)
  // 3
  afterNode.next = newNode
  size++
  return newNode
}

위 코드를 보면, afterNode 뒤에 원하는 node를 삽입하는 것을 알 수 있으며, 다음 노드에 대한 정보만 바꾸는 작업을 하므로 시간 복잡도는 O(1)임을 알 수 있다.

연결리스트에서 값을 삭제하는 방식에도 3가지가 있다.
1. pop은 연결리스트에서 맨 앞의 값을 삭제한다.
2. removeLast는 연결리스트의 맨 마지막 값을 삭제한다.
3. removeAfter는 연결리스트의 특정 위치의 값을 삭제한다.

여기서도 가장 중요한 removeAfter만 다뤄볼려고 한다.

removeAfter

fun removeAfter(node: Node<T>): T? {
  val result = node.next?.value
  
  if (node.next == tail) {
	 tail = node 
  }
  
  if (node.next != null) {
  	 size-- 
  }
  
  node.next = node.next?.next
  return result
}

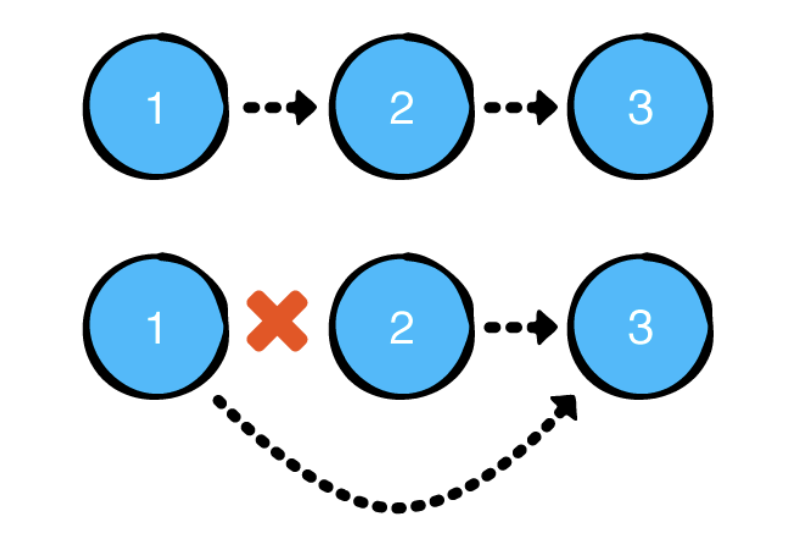
연결리스트의 특정 원소를 삭제하는 작업의 시간복잡도 또한 O(1)임을 알 수 있다.

요약

연결리스트는 선형적이며, 단방향이다. 한 노드에서 다른 노드로 참조를 이동하는 순간 이를 되돌릴 수는 없다.
연결리스트는 head-first 삽입에 대해 O(1) 시간 복잡도를 가집니다. 배열은 헤드 우선 삽입에 대해 O(n) 시간 복잡도를 가진다.
Iterable 및 Collection과 같은 Kotlin 컬렉션 인터페이스를 따르는 것은 합리적으로 적은 양의 요구 사항에 유용한 여러 메서드를 제공한다는 것을 의미한다.

의견

결국 연결리스트 자료구조는 데이터를 추가하거나, 삭제하는 경우가 빈번한 상황에 사용하면 적절할 것 같다.

그러나, 데이터를 탐색하는 과정에서, index를 통한 배열의 데이터 접근 방식과 달리, 연결리스트는 처음부터 순차 탐색을 통해 데이터를 찾기 때문에, O(n)의 시간복잡도를 갖게 된다.

여기서 오해를 많이 하는 부분이 생긴다.

연결리스트에서 데이터를 추가하는 행위는 노드가 가지고 있는 메모리 주소 값만 교체하면 되기 때문에 시간복잡도는 O(1)이지만, 추가하려는 데이터의 위치가 만약 맨 처음이 아니라 연결리스트 의 어느 중간에 있는 인덱스라면 어떨까?

결국, 연결리스트에서도 이 경우에는 순차 탐색을 하면서 해당 위치까지 가야하므로, O(n)의 시간복잡도를 갖게 된다. 즉, 연결리스트에서 추가하려는 데이터의 위치가 맨 앞일 경우에만, O(1)의 시간복잡도를 갖게 된다는 것이다.

이와 달리 배열의 경우에는 데이터들이 순차적으로 저장이 되어있다. 따라서 추가하려는 데이터의 위치가 맨 뒤가 아니라면, 추가되는 데이터 위치 이후에 있는 모든 데이터들을 한 칸씩 뒤로 미뤄야 하므로 O(n)의 시간복잡도를 갖게 된다. 다만, 추가하려는 데이터의 위치가 맨 뒤이고, 공간이 남아있다면, O(1)의 시간복잡도를 갖게 될 것이다.

데이터를 추가하는 케이스 외에도, 삭제하는 경우에서도 연결리스트와 배열은 비슷한 양상을 보인다. 즉, 어느 누구가 더 뛰어난 자료구조라고 볼 수 없을 것 같다.

정리하자면, 연결리스트는 노드가 있기 떄문에 데이터의 추가, 삭제로부터 자유로워질 수 있었지만, 대신 탐색이 느려졌다.

배열은 연속적으로 메모리를 할당받아서 데이터를 저장하기 때문에 탐색은 굉장히 빠르다. 대신에 데이터의 추가, 삭제로부터 절대 자유로울 수 없다.