Diffie–Hellman의 복잡한 수식을 간소화 하여 최대한 이해하기 쉽게 정리해보자!
1. 비대칭/대칭키 구조
우선적으로 비대칭/대칭키 구조의 차이점을 알아보자.
1-1. 비대칭키 (RSA)
비대칭키는 공개키와 개인키, 서로 다른 두 개의 키를 사용하는 방식이다.
공개키 → 비밀키 (암/복호화)
PKI나 어떤 방식을 통해 상대방의 공개키를 획득한다. A가 B의 공개키로 데이터를 암호화하면, 오직 B의 개인키로만 복호화할 수 있다.
공격자가 공개키를 탈취해도 개인키 없이는 복호화가 불가능하다. 따라서 기밀성을 보장하는 방식이다.
하지만 공격자가 본인의 공개키로 거짓 정보를 생성하면 어떻게 될까? 즉, 신원을 확인해야 하는 경우 "전자 서명" 방식을 사용해야 한다.
비밀키 → 공개키 (전자 서명)
A는 메시지 자체가 아니라 메시지 해시값을 개인키로 서명한다. (해시값이 빠른 연산에 유리)
B는 A의 공개키로 서명을 검증하고, 자신이 계산한 해시와 비교한다. 일치한다면 메시지는 A가 보낸 것이고 변조되지 않았다는 사실을 확인할 수 있다. 따라서 인증과 무결성을 보장하는 방식이다.
즉, RSA는 소수 기반 모듈러 연산을 통해 공개키/개인키 쌍을 생성하고, 이를 암호화와 서명 검증에 활용하는 대표적인 비대칭키 알고리즘이다.
1-2. 대칭키 (AES)
대칭키는 암호화와 복호화에 동일한 키를 사용하는 방식이다.
세션키 → 세션키 (암/복호화)
암/복호화에 모두 같은 키를 사용하기 대칭키라고 불린다.
비대칭키는 대칭키 방식과 연산의 과정 자체가 다르다.
- 치환(Substitution), 전치(Shift), 키 혼합(XOR) 과정을 반복하는 구조
- XOR 같은 단순 연산으로 CPU에서 빠르게 동작
- 128비트 블록 단위로 병렬 처리 가능
- AES-NI 같은 CPU 하드웨어 명령어 지원 덕분에 매우 효율적
대칭키 방식은 매우 단순하며 CPU 친화적이기에 대용량 데이터 암호화에 최적화되어 있다.
2. RSA vs Diffie–Hellman
RSA는 데이터 암/복호화를 위한 연산 알고리즘이지만, Diffie-Hellman 은 암호화 키, 정확히는 안전하게 세션키 교환을 위한 방식을 정의한 것이다.
이는 암호화 통신을 하는 A와 B가 직접적으로 키를 주고 받지 않고, 각자의 비밀값을 계산하여 "같은 대칭(세션)키"를 생성하는 것
2-1. Diffie-Hellman 키 교환 방식
1976년, Diffie는 Key를 직접 보내지 않아도 공통의 비밀 키를 공유할 수 있는 방식을 고안해냈다.
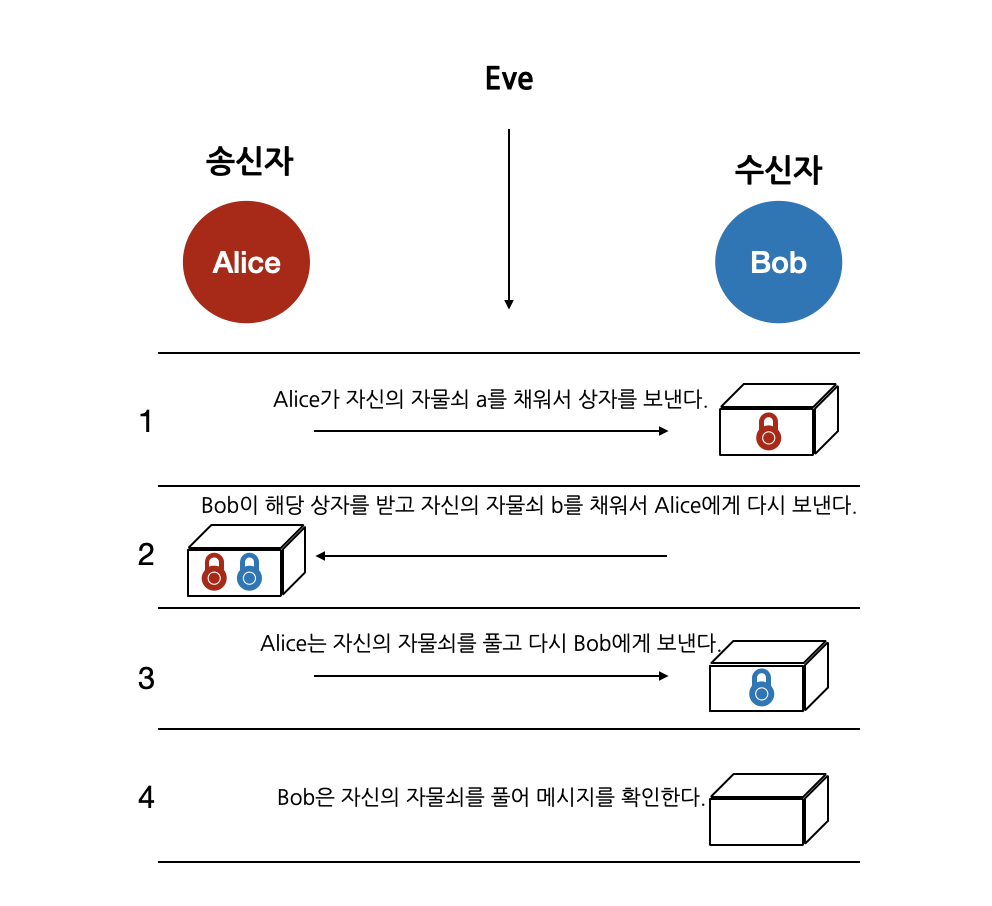
A와 B는 다음의 순서로 상자를 주고 받는다.
- A는 자신의 비밀키로 자물쇠를 채운다.
- B는 자신의 비밀키로 자물쇠를 채운다.
- A는 자신의 비밀키로 자물쇠를 해제한다. (상자에는 B의 자물쇠만 존재)
- B는 자신의 비밀키로 자물쇠를 해제한다.
이 과정은 서로 비밀키를 공유하지 않았지만 상자를 안전하게 전달할 수 있다.
그러나, 통신을 2번이나 해야하는 단점이 있는데, 이를 보완하고자 나온 것이 바로 DH키 교환 방식이다.
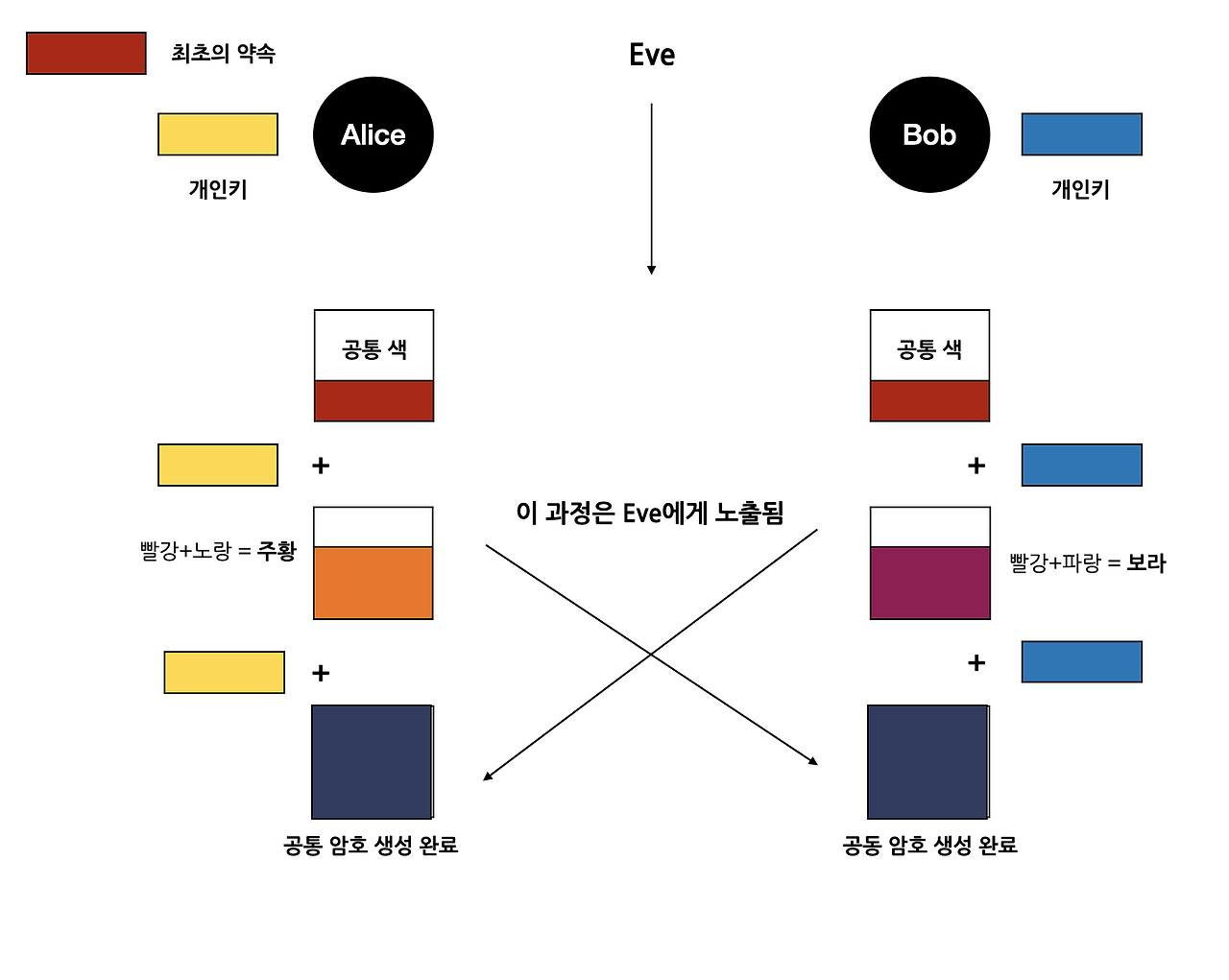
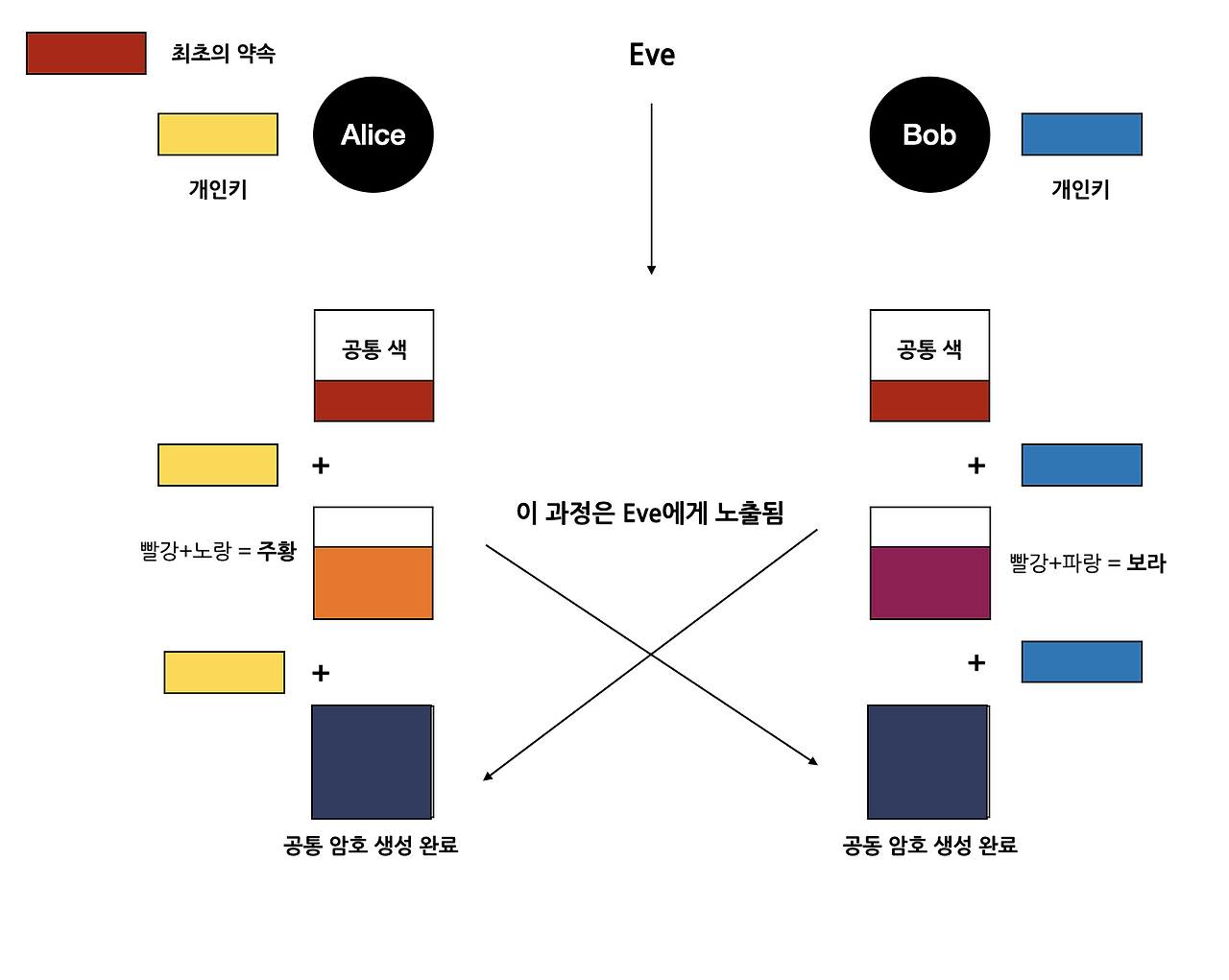
A와 B는 약속된 공통된 값(빨강)을 기준으로 잡고 각자의 개인키(노랑, 파랑)를 약속된 공통값에 섞는다.
그리고 이를 서로 주고받는다. 공격자는 이 중간 값을 봐도 이해할 수 없음.
서로 주고받은 공통값에 자신의 색을 섞는다. A는 빨강+파랑을 받았고 자신의 개인키인 노랑을 섞어 빨+파+노
B는 빨강+노랑을 받았고 자신의 개인키은 파랑을 섞어 빨+파+노.
즉, (빨+파+노) 라는 같은 대칭키 가지게 된다.
2-2. Diffie–Hellman의 예시
-
공통으로 약속한 값:
- 소수 𝑝 = 23
- 원시근 𝑔 = 5 -
A(노랑, 개인 비밀키) = 6
-
B(파랑, 개인 비밀키) = 15
여기서, 공통으로 약속한 값은 TLS의 "Server Key Exchange" 과정에서 파라미터로 전달된다.
1. 공개키 계산 (서로 주고받는 값)
- A →
g^a mod p = 5^6 mod 23 = 15625 mod 23 = 8 - B →
g^b mod p = 5^15 mod 23 = 30517578125 mod 23 = 19
이 때 네트워크에 흘러가는 건 단순히 8과 19
2. 공유 비밀 계산
- A →
19^6 mod 23 = 2 - B →
8^15 mod 23 = 2
둘 다 2라는 동일한 값(공유 비밀)을 얻게 된다.
3. 공격자가 본 정보
p=23, g=5, A→8, B→19 전부 알 수 있지만, A와 B만 알고있는 지수 a=6, b=15를 역산하는 건 이산 로그 문제로서 작은 숫자라면 brute-force 로 풀 수 있지만, 실제 TLS에서는 p가 수백 자리 소수라 사실상 불가능에 가깝다고 한다.
쉬운 설명
공격자는 빨강(=23, 공통 약속 값)과 섞인 값 빨강+파랑(=8), 빨강+노랑(=19) 까지 다 볼 수 있고, 노랑(=6), 파랑(=15)은 네트워크 상에 흘러가지 않기 때문에 볼 수 없다.
섞인 값을 기반으로 ‘노랑(=6), 파랑(=15)’로 역산하는 건 수학적으로 너무 어려워 사실상 불가능하다고 한다.
3. 결론
RSA는 공개/개인키 기반의 비대칭키 암호화 알고리즘이며 데이터 암호화/전자서명에 사용된다.
Diffie–Hellman은 직접 키를 교환하지 않고 같은 세션키를 합의하는 방식으로 안전한 대칭키 통신의 기반이다.
오늘날 TLS에서는 두 가지가 결합되어, 빠르면서도 안전한 인터넷 암호화 통신이 가능하다!
3-1. TLS에서의 활용
실제 TLS(HTTPS) 통신에서는 다음 조합으로 사용된다.
- Diffie–Hellman(ECDHE) → 세션키 합의
- RSA/ECDSA → 서버 신원 검증(전자서명)
- AES/ChaCha20 → 실제 데이터 암호화
최근에는 비대칭키 방식으로 키를 교환하고 세션키 방식으로 암/복호화를 진행할 때, "비대칭키 방식으로 키를 교환"하는 RSA 방식을 안쓰고 Diffie–Hellman 을 쓴다고 한다.
참고문헌
[암호학] 암호학의 미궁 - 암호학의 발달 과정, Diffie-Hellman, RSA, 공개키 암호화