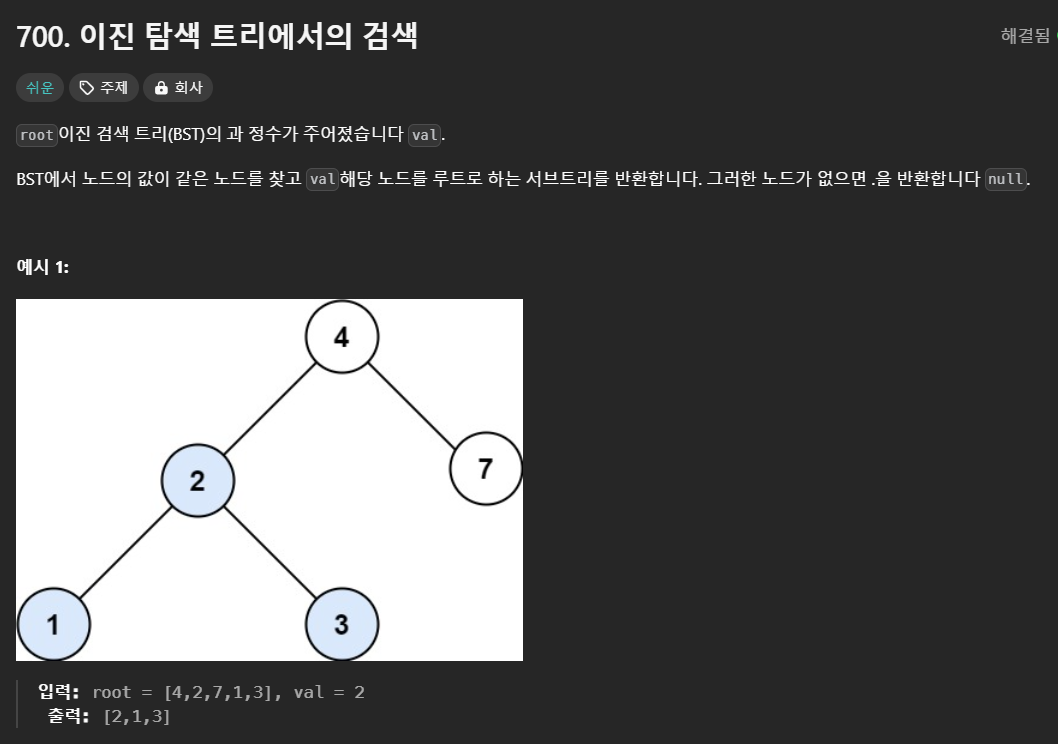
이진탐색

✏️오늘의 문제

💡나의 풀이

---

  class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int x) {
        val = x;
    }
}


class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        // 기저 사례: root가 null이거나 val을 찾은 경우
        if (root == null || root.val == val) {
            return root;
        }
        
        // val이 현재 노드의 값보다 작으면 왼쪽 서브트리에서 탐색
        if (val < root.val) {
            return searchBST(root.left, val);
        }
        // val이 현재 노드의 값보다 크면 오른쪽 서브트리에서 탐색
        else {
            return searchBST(root.right, val);
        }
    }
}

이진 탐색 트리의 노드 탐색 구현

이 코드는 이진 탐색 트리(BST)에서 특정 값을 찾는 재귀 함수를 구현한 예제입니다. 이진 탐색 트리는 노드가 왼쪽 서브트리에 있는 모든 값이 현재 노드의 값보다 작고, 오른쪽 서브트리에 있는 모든 값이 현재 노드의 값보다 큰 특성을 가지고 있습니다. 이 특성을 활용하여 효율적으로 값을 탐색할 수 있습니다.

TreeNode 클래스 설명

class TreeNode {
    int val; // 노드의 값
    TreeNode left; // 왼쪽 자식 노드
    TreeNode right; // 오른쪽 자식 노드
    
    TreeNode(int x) {
        val = x; // 생성자에서 노드의 값을 초기화
    }
}

• val: 노드의 값을 저장하는 정수형 변수입니다.
• left: 왼쪽 자식 노드에 대한 참조입니다.
• right: 오른쪽 자식 노드에 대한 참조입니다.
• 생성자: TreeNode 객체를 생성할 때 값(x)을 초기화합니다.

이 TreeNode 클래스는 이진 탐색 트리를 구성하는 기본 단위로, 트리의 각 노드는 자신이 가진 값과 두 개의 자식 노드에 대한 정보를 가지고 있습니다.

Solution 클래스 설명

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        // 기저 사례: root가 null이거나 val을 찾은 경우
        if (root == null || root.val == val) {
            return root;
        }
        
        // val이 현재 노드의 값보다 작으면 왼쪽 서브트리에서 탐색
        if (val < root.val) {
            return searchBST(root.left, val);
        }
        // val이 현재 노드의 값보다 크면 오른쪽 서브트리에서 탐색
        else {
            return searchBST(root.right, val);
        }
    }
}

• searchBST 메서드: 이 메서드는 이진 탐색 트리에서 주어진 값(val)을 찾습니다.
  • 기저 사례: root가 null이거나 현재 노드의 값이 val과 같다면 해당 노드를 반환합니다. 이는 탐색이 종료되는 조건입니다.
  • 왼쪽 서브트리 탐색: 찾고자 하는 값(val)이 현재 노드의 값보다 작으면 왼쪽 서브트리에서 탐색합니다.
  • 오른쪽 서브트리 탐색: 찾고자 하는 값이 현재 노드의 값보다 크면 오른쪽 서브트리에서 탐색합니다.

이 알고리즘은 이진 탐색 트리의 특성을 활용하여 평균적으로 O(log n)의 시간 복잡도로 값을 찾을 수 있습니다. 그러나 최악의 경우(예: 트리가 일렬로 늘어선 경우)에는 O(n)의 시간 복잡도가 될 수 있습니다.