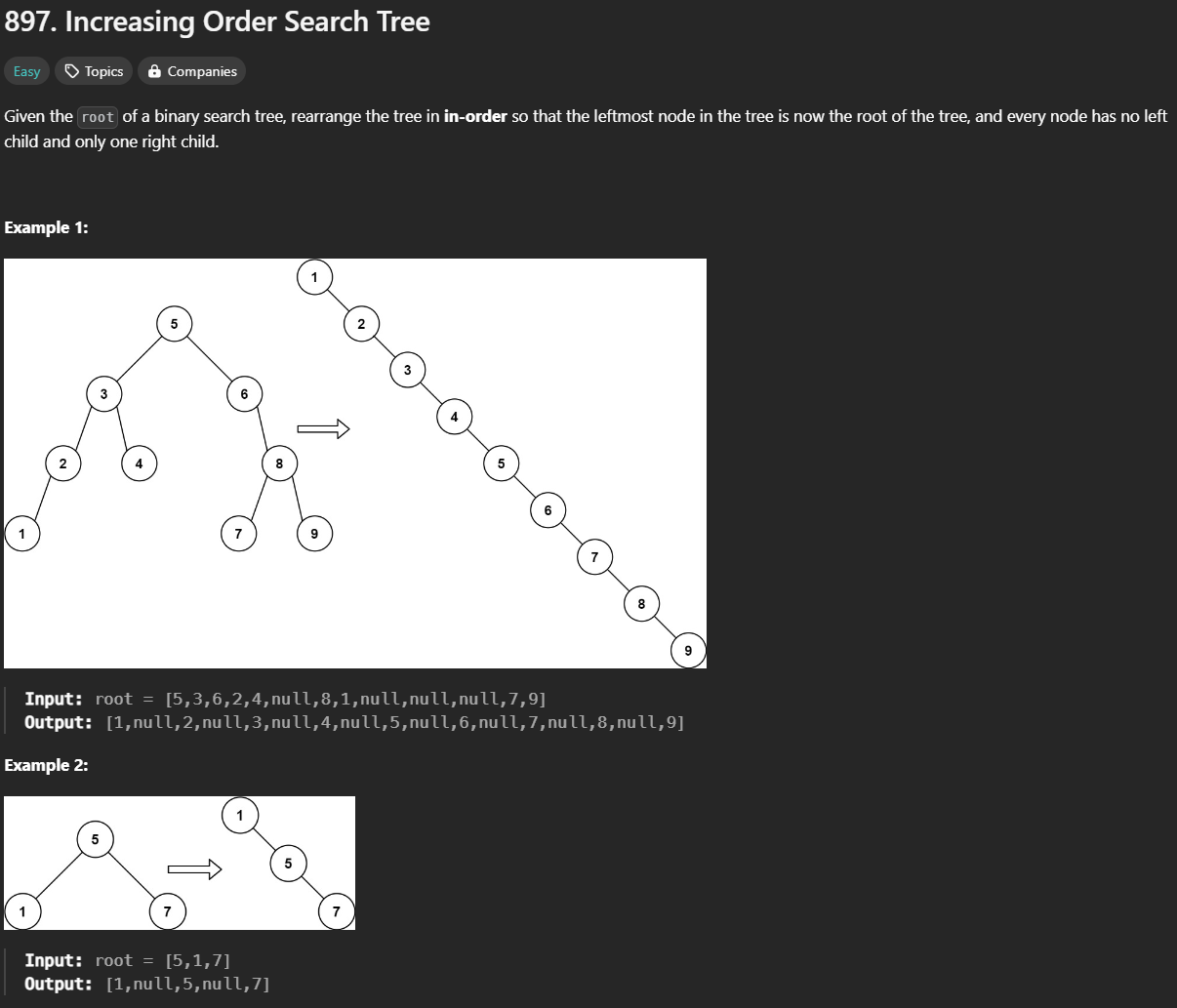
Increasing Order Search Tree

✏️오늘의 문제

💡풀이

---

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}


class Solution {
    private TreeNode newRoot = null;
    private TreeNode current = null;
    
    public TreeNode increasingBST(TreeNode root) {
        inOrderTraversal(root);
        return newRoot;
    }
    
    private void inOrderTraversal(TreeNode node) {
        if(node == null) return;
        
        inOrderTraversal(node.left);
        
        if(newRoot == null) {
            newRoot = new TreeNode(node.val);
            current = newRoot;
        } else {
            current.right = new TreeNode(node.val);
            current = current.right;
        }
        
        inOrderTraversal(node.right);
    }
}

주요 구성 요소

1. TreeNode 클래스

   • 이 클래스는 이진 트리의 노드를 정의합니다.
   • val: 노드의 값을 저장합니다.
   • left: 왼쪽 자식을 가리키는 포인터입니다.
   • right: 오른쪽 자식을 가리키는 포인터입니다.
   • 세 가지 생성자를 제공하여 다양한 방법으로 노드를 생성할 수 있습니다.

2. Solution 클래스

   • 이 클래스는 트리를 변환하는 로직을 포함하고 있습니다.
   • newRoot: 새로운 트리의 루트를 저장하는 변수입니다.
   • current: 새로운 트리에서 현재 위치를 추적하는 변수입니다.

메서드 설명

1. increasingBST(TreeNode root)

• 입력: 기존 이진 탐색 트리의 루트 노드.
• 작업: inOrderTraversal 메서드를 호출하여 트리를 중위 순회합니다.
• 출력: 새로 생성된 트리의 루트 노드(newRoot)를 반환합니다.

2. inOrderTraversal(TreeNode node)

• 입력: 현재 노드.
• 작업:
  • 재귀적으로 왼쪽 서브트리를 방문합니다.
  • 현재 노드의 값을 처리합니다.
    • newRoot가 null인 경우, 새로운 노드를 생성하고 newRoot와 current를 설정합니다.
    • 그렇지 않은 경우, 현재 노드의 오른쪽에 새로운 노드를 추가하고 current를 갱신합니다.
  • 마지막으로 오른쪽 서브트리를 방문합니다.

작동 원리

• 이 코드의 핵심은 중위 순회입니다. 이진 탐색 트리를 중위 순회하면 노드를 오름차순으로 방문하게 됩니다.
• newRoot가 null일 때는 새로운 트리의 시작점이 되며, 이후에는 current를 통해 새로운 노드를 계속 추가합니다.
• 최종적으로, increasingBST 메서드는 새로운 트리의 루트를 반환합니다. 이 트리는 모든 노드가 오른쪽으로만 연결된 형태로, 각 노드는 오름차순으로 정렬되어 있습니다.

💡 더 간결한 풀이

---

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {}

    TreeNode(int val) { 
        this.val = val; 
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    private TreeNode dummy = new TreeNode(0); // 더미 노드
    private TreeNode current = dummy; // 현재 노드

    public TreeNode increasingBST(TreeNode root) {
        inOrderTraversal(root);
        return dummy.right; // 더미 노드의 오른쪽 자식 반환
    }

    private void inOrderTraversal(TreeNode node) {
        if (node == null) return;

        inOrderTraversal(node.left); // 왼쪽 서브트리 방문

        // 현재 노드의 값을 새로운 노드에 추가
        current.right = new TreeNode(node.val);
        current = current.right; // 현재 노드 갱신

        inOrderTraversal(node.right); // 오른쪽 서브트리 방문
    }
}

현재 제공된 코드도 이진 탐색 트리를 오름차순으로 변환하는 데 효율적이지만, 더 간결하게 작성할 수 있는 방법이 있습니다. 특히, 새로운 트리를 생성하는 과정에서 불필요한 객체 생성을 줄이고, 메모리를 효율적으로 사용할 수 있습니다.

개선 사항 설명

1. 더미 노드 사용:

   • dummy 노드를 사용하여 새로운 트리의 시작점을 쉽게 관리할 수 있습니다. 이로 인해 newRoot 변수를 별도로 관리할 필요가 없습니다.
   • current는 항상 dummy의 오른쪽 자식을 가리키므로, 새로운 노드를 추가할 때 current를 갱신하는 작업이 더 직관적입니다.

2. 코드 간결성:

   • 불필요한 조건문을 줄였고, 새로운 노드를 추가하는 과정이 간결해졌습니다.
   • newRoot를 초기화하는 과정이 필요 없어져 코드가 더욱 깔끔해졌습니다.

성능

이 개선된 코드는 기존 코드와 동일한 시간 복잡도(O(n))를 유지하며, 메모리 사용 측면에서도 더 효율적입니다. 더미 노드를 통해 초기화 및 관리가 용이해져 가독성도 향상되었습니다.