문제 링크

합승 택시 요금

문제 설명

무지는 택시비를 아끼기 위해서 어피치와 적절히 합승하려고 한다.

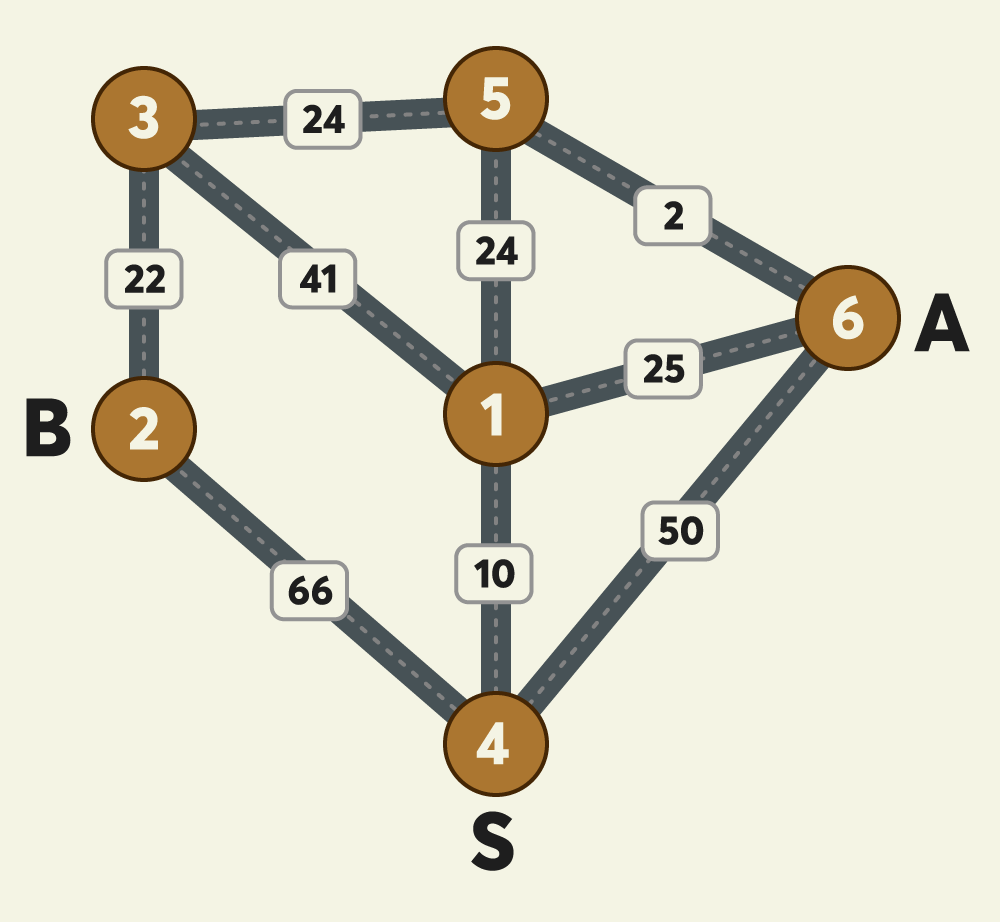
위 예시 그림은 6개의 지점 사이 택시 노선과 예상 요금을 나타낸다. 무지의 집이 A, 어피치의 집이 B라고 할때, 두 사람은 출발지점 S에서 택시를 타고 귀가하려고 한다. 두 사람이 모두 귀가하는 데 소요되는 예상 최저 택시요금이 얼마인 지 계산하려고 한다.

이 경우에서의 최저 요금은

4→1→5 : A, B가 합승하여 택시를 이용합니다. 예상 택시요금은 10 + 24 = 34원 입니다.
5→6 : A가 혼자 택시를 이용합니다. 예상 택시요금은 2원 입니다.
5→3→2 : B가 혼자 택시를 이용합니다. 예상 택시요금은 24 + 22 = 46원 입니다.
A, B 모두 귀가 완료까지 예상되는 최저 택시요금은 34 + 2 + 46 = 82원 입니다.

이와 같이 노선과 지점들 사이의 요금이 주어졌을때, 최저 예상 택시요금을 계산해서 return 하도록 solution 함수를 완성하라. 만약, 아예 합승을 하지 않고 각자 이동하는 경우의 예상 택시요금이 더 낮다면, 합승을 하지 않아도 된다.

문제 풀이

다익스트라를 적절히 활용해서 풀면 된다.

1. 두 사람 시작점에서 각자 택시타고 집으로 이동하는 경우 계산 -> 다익스트라

distance = [INF]*(n+1) #최단 거리 테이블
dijkstra(s, distance, graph)
    #경우1) 각자 택시 따로 타기

2. 두 사람이 시작점에서 특정 지점까지 합승하고 이후, 각자 집까지 이동하는 경우 계산 -> 다익스트라 2번

#경우2) 특정 지점까지 같이 타고 이후 각자 집까지
    for i in range(n+1):
        cost = 0
        distance_a = [INF]*(n+1)
        distance_b = [INF]*(n+1)
        if i != s:
            cost += distance[i]
            dijkstra(i, distance_a, graph)
            dijkstra(i, distance_b, graph)
            cost = cost + distance_a[a] + distance_b[b]
            answer = min(answer, cost)

전체 코드

import heapq

INF = int(1e9)

def dijkstra(start, distance, graph):
    #시작 노드 처리
    pq = []
    heapq.heappush(pq, (0, start))
    distance[start] = 0

    while pq:
        dist, now = heapq.heappop(pq)
        #현재 노드가 이미 처리된 적 있는 노드면,
        if distance[now] < dist:
            continue
        #아니면,
        for i in graph[now]:
            cost = distance[now] + i[1]
            if cost < distance[i[0]]:
                distance[i[0]] = cost
                heapq.heappush(pq, (cost, i[0]))

def solution(n, s, a, b, fares):
    graph = [[] for _ in range(n+1)] #노드 연결 정보
    distance = [INF]*(n+1) #최단 거리 테이블

    for c,d,f in fares:
        graph[c].append((d,f))
        graph[d].append((c,f))
    
    dijkstra(s, distance, graph)
    #경우1) 각자 택시 따로 타기
    answer = distance[a] + distance[b]
    #경우2) 특정 지점까지 같이 타고 이후 각자 집까지
    for i in range(n+1):
        cost = 0
        distance_a = [INF]*(n+1)
        distance_b = [INF]*(n+1)
        if i != s:
            cost += distance[i]
            dijkstra(i, distance_a, graph)
            dijkstra(i, distance_b, graph)
            cost = cost + distance_a[a] + distance_b[b]
            answer = min(answer, cost)
    return answer

느낀점

다익스트라의 구현이 안떠올라서 옛날에 정리해둔거 보고 풀었다,, 최단거리 알고리즘들 날잡고 한번 복습 해야될둣