LIS란?

• Longest Increasing Subsequence
• 한 수열에서 특정 부분을 지워서 만들 수 있는 최장 증가 부분 수열
  e.g. 백준 11053 -가장 긴 부분 증가 수열
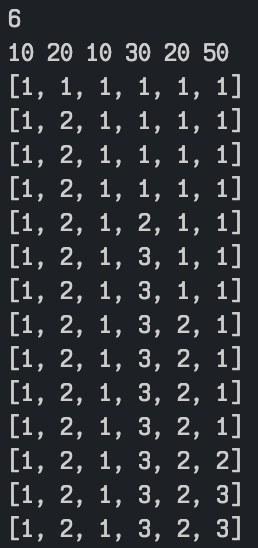
  [10, 20, 10, 30, 20, 50] 의 리스트가 주어졌을때
  -> LIS : [10, 20, 30, 50]

구현하기

방법 1) 완전탐색 $O(2^N)$

: 모든 증가 부분 수열을 만들어서 길이가 최대인거 고르기
shoark7님의 블로그 설명을 참고했습니다.

def lis_bf(seq):
    if not seq:
        return 0
    ret = 1
    for i in range(len(seq)):
        next = []
        for j in range(i+1, len(seq)):
            if seq[i] < seq[j]:
                next.append(seq[j])
        ret = max(ret, 1+lis_bf(next))
    return ret

방법 2) DP $O(N^2)$

LIS의 길이 구하기

• dp[i] : seq[:i+1]의 LIS 길이

def lis_dp(N):
    dp = [1]*N
    #LIS 알고리즘
    for i in range(1, N):
        for j in range(0, i):
            if seq[i] > seq[j]:
                dp[i] = max(dp[i], dp[j]+1)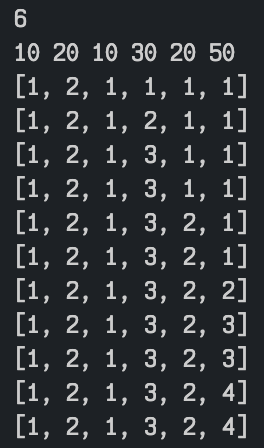

백준 11053 -가장 긴 부분 증가 수열 tc 입력에 대해서 위와 같이 dp가 계산되는것을 확인할 수 있다.

• seq[i] > seq[j]
  : LIS의 조건
• dp[i] = max(dp[i], dp[j]+1)
  : seq[:j+1]까지의 LIS길이 + i의 길이 1

LIS 역추적하기

위의 코드로는 실제 LIS가 어떤 숫자들로 이루어져있는지 알 수 없다. 역추적하기 위해서는 dp배열을 LIS의 길이와 일치하는 값을 가지는 인덱스부터 거꾸로 탐색한다.

order = max(dp)
answer = []

for i in range(N-1, -1, -1):
    if dp[i] == order:
        answer.append(seq[i])
        order -= 1
answer.reverse()

방법 3) 이분탐색 $O(NlogN)$

seungkwan님의 포스팅을 참고해서 공부했습니다.
앞의 방법2 DP를 이용한 방법은 seq[:i+1]에서 지금까지의 LIS길이 중 최대값을 찾기 위해 0~i-1까지 순회해야 한다. -> $O(N)$
-> 위를 이분탐색으로 접근해서 $O(logN)$시간 안에 찾아보자,,,

dp[i] : 길이가 i인 LIS를 만들 수 있는 원소중 제일 작은 값

dp = [seq[0]]

for i in range(len(seq)):
    if dp[-1] < seq[i]:
        #현재까지의 LIS 마지막 원소보다 지금 보고있는 값이 더 크면 LIS+[seq[i]]의 새 LIS
        dp.append(seq[i])
    else:
        #seq[i]가 들아갈 위치 찾기
        idx = bisect_left(dp, seq[i])
        dp[idx] = seq[i]

출처

https://seungkwan.tistory.com/8
https://shoark7.github.io/programming/algorithm/3-LIS-algorithms

LIS 연습 풀면서 더 추가해보겠읍니다..