1. Getting Dtarted with Graphs

1.1 Technical requirements

1.2 Introduction to graphs with networkx

그래프 이론에 대한 일반적인 소개

simple undirected graph(무방향 그래프)

$G=(V,E)$

$V=\{V_1,\dots, V_n\}$
: 노드(혹은 정점)들의 집합

$E=\{\{V_k,V_W\},\dots,\{V_i,V_j\}\}$
: 엣지(혹은 링크)들의 두-집합(두 요소들의의 집합)들의 집합

$E$ 의 각 원소가 2집합이므로 각 엣지 사이에 순서가 없음. 즉, $\{V_k,V_W\}$ 와 $\{V_w,V_k\}$는 동일한 엣지.

그래프 및 노드의 일부 기본 속성에 대한 정의

• 그래프의 순서
  : 노드 개수 $\vert V \vert$
• 그래프의 크기
  : 엣지 개수 $\vert E \vert$
• 노드의 차수
  : 인접한 엣지 개수
• 노드의 이웃
  : 그래프 $G$에서 정점 $v$의 이웃은 $v$에 인접한 모든 정점에 의해 유도된 정점 $V'$의 부분 집합
• 이웃 그래프(자아 그래프)
  : 그래프 $G$에서 정점 $v$의 이웃 그래프(자아 그래프)는 $v$에 인접한 정점과 연결하는 모든 엣지로 구성된 $G$의 하위 그래프

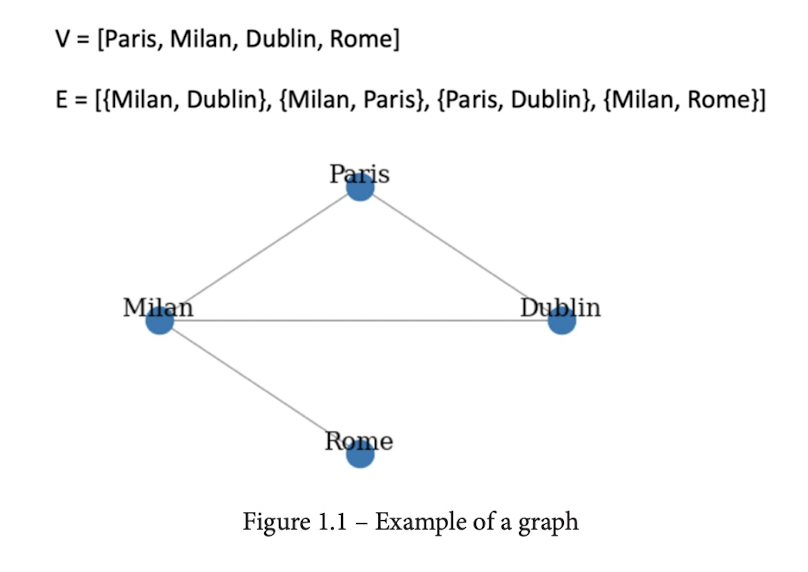
방향이 없기 때문에 밀라노에서 파리까지의 엣지와 파리에서 밀라노까지의 엣지가 같음. 따라서 제약없이 양방향 이동 가능.

그래프의 속성

• 그래프의 순서
  : 4 (노드 4개)

• 그래프의 크기
  : 4 (엣지 4개)

• 각 노드의 차수
  - Paris: 2
  - Milan: 3
  - Dublin: 2
  - Rome: 1

• 각 노드의 이웃
  - Paris = {Milan, Dublin}
  - Milan = {Paris, Dublin, Rome}
  - Dublin = {Paris, Milan}
  - Rome = {Milan}

1.2.1 Types of graphs

1.2.1.1 Digraphs

1.2.1.2 Multigraph

1.2.1.3 Weighted graphs

1.2.1.4 Bipartite graphs

1.2.2 Graph representations

1.2.2.1 Adjacency matrix

1.2.2.2 Edge list

1.3 Plotting graphs

1.3.1 networkx

1.3.2 Gephi

1.4 Graph properties

1.4.1 Integration metrics

1.4.2 Segregation metrics

1.4.3 Centrality metrics

1.4.4 Resilience metrics