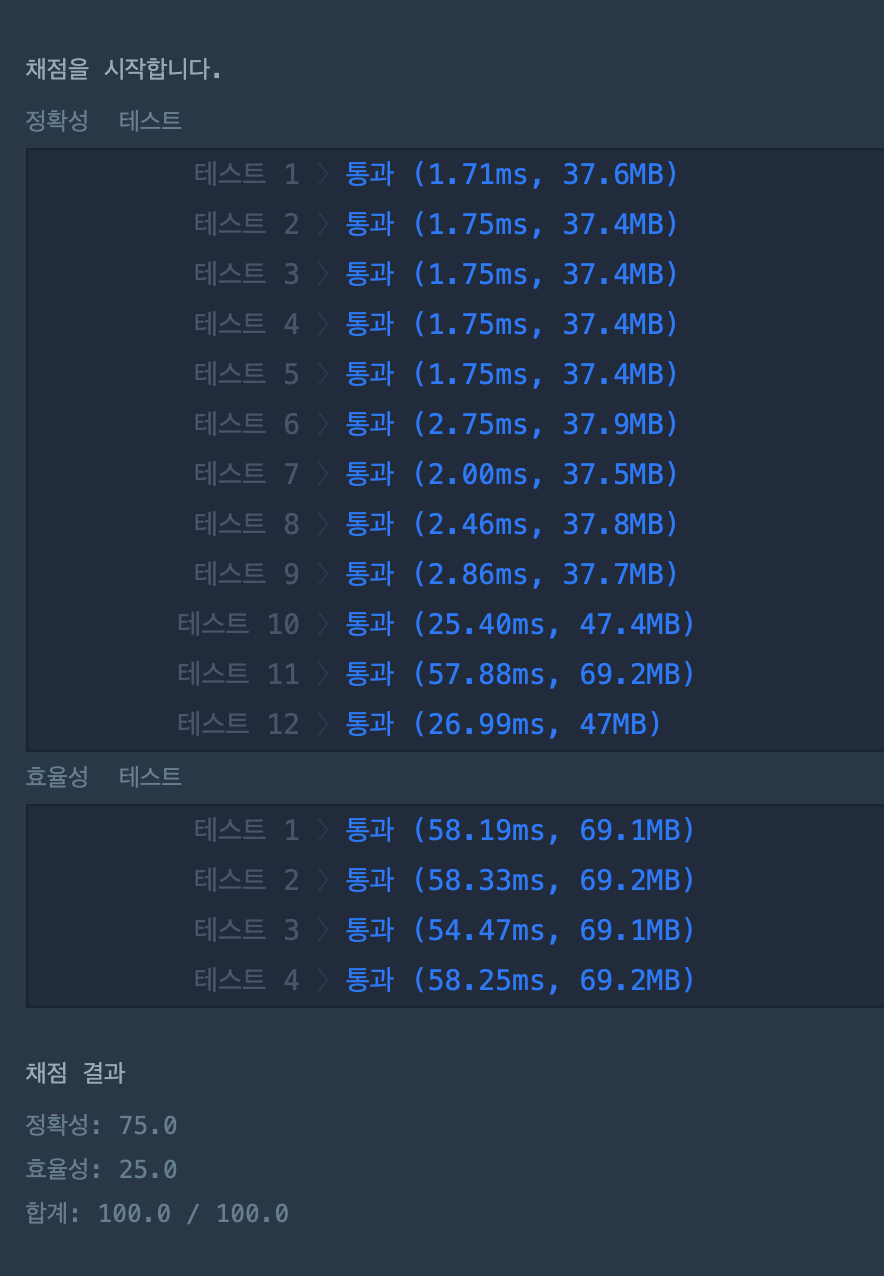
Algorithm Problem with JavaScript — 3day
Problem
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)
제한사항
- n은 2이상 1000000이하의 자연수입니다.
입출력 예
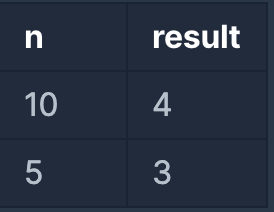
입출력 예 설명
입출력 예 #1
1부터 10 사이의 소수는 [2,3,5,7] 4개가 존재하므로 4를 반환
입출력 예 #2
1부터 5 사이의 소수는 [2,3,5] 3개가 존재하므로 3를 반환
1. 문제 이해하기
주어진 n까지의 소수가 몇 개인지 찾으면 된다. n은 1000000 이하의 자연수이다. 최대 1000000일 경우, O(n)의 시간복잡도도 통과 못 할 수 있다. 따라서 시간복잡도가 O(n) 이하가 되도록 함수를 구성해야 한다. logN또는 √n 의 시간복잡도를 가져야 한다.
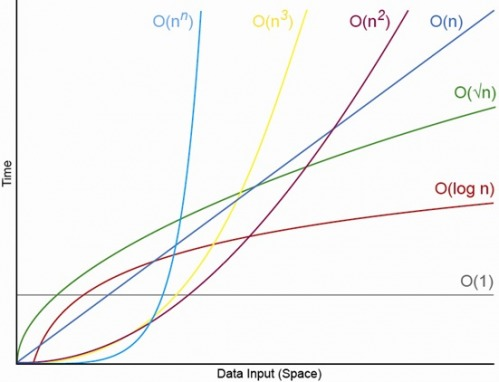
에라토스테네스의 체 원리를 이용하면 시간복잡도를 √n으로 해결할 수 있다.
2. 해결 방법
에라토스테네스의 체
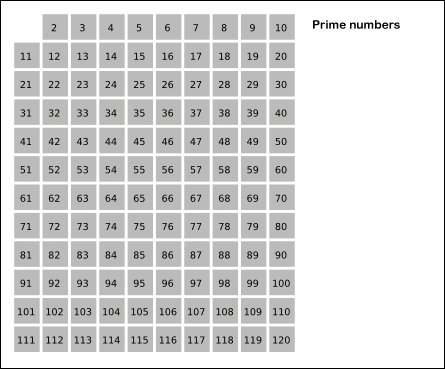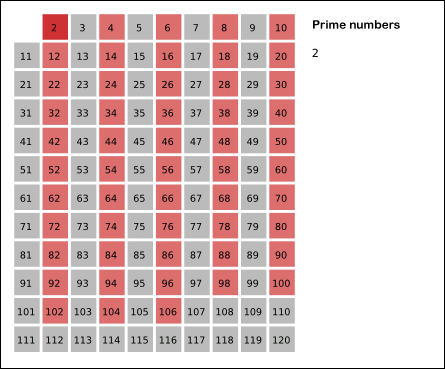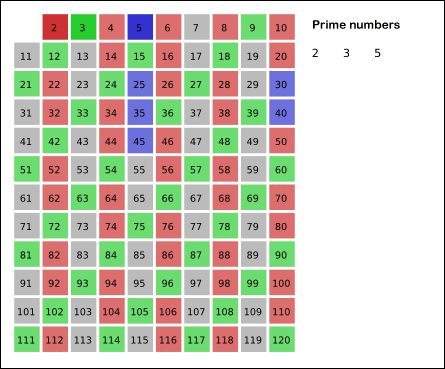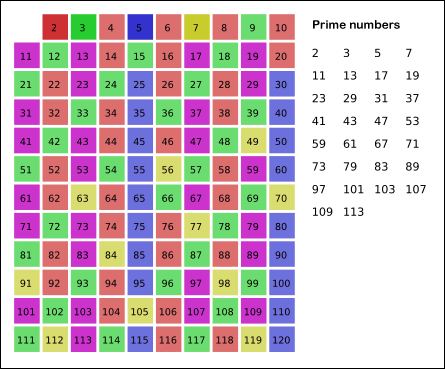
1을 제외하고 2부터 순차적으로 N까지 자신을 제외하고 자신의 배수들을 차례대로 지워가면 결국에는 소수들만 남는다는 원리이다. 여기서 N까지가 아니라 √N까지만 검사해도 결과는 같다.
예를 들어 N = 16 일 때를 생각해보자.
1은 소수가 아니니까 1은 제외하고 2부터 실행한다.
2는 자신을 제외한 2의 배수를 모두 제거한다.
[4,6,8,10,12,14,16] 를 모두 삭제한다.
다음은 3이다. 3을 제외한 3의 배수를 제거한다.
[6,9,12,15]를 삭제한다.(12는 이전에 삭제)
4는 이미 삭제되었다.
다음은 5이다. 5를 제외한 5의 배수를 삭제한다.
[10,15] 모두 이미 삭제되었다.
10은 5의 배수이면서 2의 배수이다.
15는 5의 배수이면서 3의 배수이다.
즉, 5의 배수는 25(5의 제곱)가 나오기 전까지 모든 5의 배수는 이미 삭제되었다.
따라서 √16(4)까지만 검사하면 된다. √16(4) 이후의 배수들은 이미 삭제되어 있기 때문에 신경 쓸 필요가 없다.
코드 구현 아이디어
1부터 N까지 들어간 배열을 만든다. 2부터 √N까지 반복문을 돌면서 안에서 해당의 숫자의 배수들을 0으로 만든다.(자연수 처리를 위해서 i < √N 대신 i^2 < N를 이용했다) 이후에 1은 소수가 아님으로 shift()로 제거하고 filter를 이용해서 0의 숫자들을 모두 제거한다. 이렇게 만들어진 배열의 길이를 리턴하면 1부터 N까지의 소수 개수를 알 수 있다.
3. 코드 구현

4. 결과 분석