[정글 week02] 백준 코테 복습 회귀 N-Queen 9663

n queen

n * n인 체스판에 n개가 서로 공격할 수 없게 놓는 문제.

1. n개의 row에 1개씩 queen이 들어가야 한다.
2. 같은 col에 queen이 있는지 확인
3. 대각선에 queen이 있는지 확인

문제 풀이

• 보드는 n개만 있으면 된다. 왜냐하면 n개만 있을지라도 인덱스를 통해 모든 보드판의 위치를 확인할 수 있다.
• 3개의 리스트가 필요하다. (리스트들의 크기는 2**n-1)
  1. col을 확인하는 리스트, 하나라도 현재 위치(row)가 2일 때 n번 반복하면서 현재 열에 queen이 있다면 False로 반환하고, 존재하지 않다면 True
  2. • 대각선 방향 [i + j]
  3. • 대각선 방향 [i - j] + n - 1, 이렇게 함으로써 모든 대각선 방향은 동일한 인덱스 값을 가지게 되므로 확인이 가능하다.
• row의 시작값은 0이 된다.
  - 왜냐하면 0번부터 n번까지 row열을 순회하기 때문.
  
• 종료 조건
  • row가 n이랑 같을 때 종료
  • 재귀 함수 호출하면서 row를 1씩 더 해간다.

코드

N = 8
boards = [0] * N

cols = [False] * (2**N-1)
plus = [False] * (2**N-1)
minus = [False] * (2**N-1)

def n_queen(row):
    if row == N:
        return 1
    
    count = 0
    for i in range(N):
    	# 백트래킹 가지치기 역할
        if not cols[i] and not plus[i + row] and not minus[i - row + N - 1]:
            cols[i] = plus[i + row] = minus[i - row + N - 1] = True
            count += n_queen(row+1) # 재귀 함수 row를 반복하면서 모든 보드를 순회한다.
            cols[i] = plus[i + row] = minus[i - row + N - 1] = False

    return count

n_queen(0)

알고리즘

백트래킹(Back Tracking)
가능한 모든 경우의 수를 시도하지만, 조건에 따라 조기 탐색을 중단한다.

시간 복잡도

최악의 경우 : O(n^2)
n * n번을 순회하기 때문에 조건에 따라 가지치기를 실행한다 할지라도 실제로 O(n^2) 보다는 작을 수 있다.

공간 복잡도

boards : O(n)
cols : O(n)
plus : O(2N-1) => O(n)
minus : O(2N-1) => O(n)
재귀 함수 : 최대 깊이 n
배열과 재귀 스택 포함하면 O(n)이 된다.

문제를 복습해 보았다.
처음에는 아예 접근하지 못해 풀지 못했던 문제.
고군분투 했는데 같이 정글에 속한 동료분들에게 설명과 구글링을 통해 정답을 알게 되어 문제는 해결했지만 완전히 이해하지 못했다.

특히 n이 4이고, 대각선 방향이
i = 0, row = 3
i-row = -3
-3 + 4 - 1 = 0

도대체 이게 의미하는 것은 무엇일까
계속 헷갈렸고 이해하기가 어려웠다.

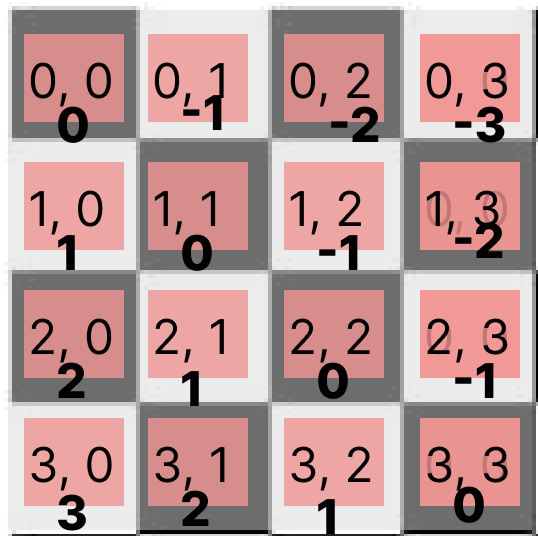
i-j 대각선 방향

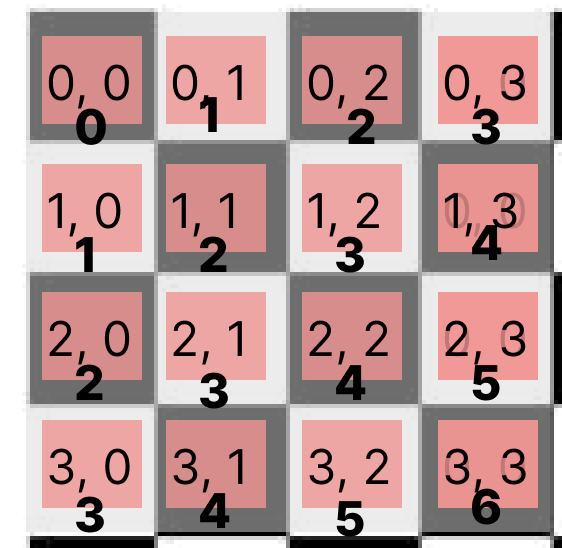
i+j 대각선 방향

서로 다른 대각선 방향을 볼 수 있다.

의미
↘ 방향 대각선: i + j가 같은 값이면 같은 대각선 상에 있다.
↙ 방향 대각선: i - j가 같은 값이면 같은 대각선 상에 있다.
결국 이를 통해 대각선 방향 충돌 여부를 확인할 수 있다.

약 1주일이 지난 현재 회귀 하고자 다시 풀어 보았다.
머릿속에 전에 풀었던 기억이 남아있는지 빠르게 문제를 정의하고 접근할 수 있었다.

하지만 여전히 위 문제에 대해 아리송한 느낌이 많이드는...그런 기분이다.
이해한 듯 하지 못한 듯.
그렇다면 이해를 하지 못한 것으로...
또 다시 일주일 뒤에 보는 것으로...