[정글 week02] 백준 코테 사냥꾼 8983

Woody Jo·2025년 5월 27일

kjungle

목록 보기

8/31

알고리즘

이분 탐색 (사대 이분 탐색을 적용한, 동물들을 완전 탐색)

시간 복잡도

sort() : O(n log n)
for ~ while : O(n log n)
결론 : O(n log n)

공간 복잡도

입력 공간 : O(m * n)
보조 공간 : O(1)

풀이 방법

distance = abs(m - x) + y <= L 이건 사대 m 중심으로 거리 계산
m in [x - (L - y), x + (L - y)] 이건 동물 기준으로 사대가 쏠 수 있는 구간을 정해주는 방식

위 사대(m) 중심으로 계산하는 공식은 맨하튼 거리의 공식이라고 한다.
하지만 사대(m) 중심이 아닌, 동물 기준으로 사대까지의 맨하튼 거리를
계산하여 풀이에 적용 하였다.

M, N, L = list(map(int, input().split()))
m_list = list(map(int, input().split()))
# 사대 정렬 - 이분 탐색 타겟
m_list.sort()
animals = []

for _ in range(N):
    x, y = list(map(int, input().split()))
    if y <= L: # 사격 거리에 위치한 데이터만 담기
        animals.append([x, y])

count = 0
for x, y in animals:
	  # 동물 기준 사대가 쏠 수 있는 왼쪽 구간 
    left_bound = x - (L - y)
	  # 동물 기준 사대가 쏠 수 있는 오른쪽 구간 
    right_bound = x + (L - y)

    left = 0
    right = len(m_list)-1
    found = False

    while left <= right:
        mid = (left + right) // 2
        if left_bound <= m_list[mid] <= right_bound:
            found = True
            # 중복 방지
            break
        elif m_list[mid] < left_bound:
            # 사대가 동물 보다 왼쪽에 위치한 경우
            left = mid + 1
        else:
            # 사대가 동물 보다 오른쪽 위치한 경우
            right = mid - 1
		# 사격 가능한 위치라면 count += 1 (중복 방지)
    if found:
        count += 1

print(count)

GPT의 도움을 많이 받아 문제를 풀 수 있었다.
그러고 팀원들간의 코어 타임 시간에 사냥꾼 문제를 다시 풀어 보았다.

내가 얼만큼 이해했는가를 생각할 수 있었다.

계속 헷갈린 부분

"사대를 반복하면서 동물들을 이진 탐색한다고 생각한다."라는 생각으로 문제를 접근했는데 팀원들과 얘기하면서 "동물들을 반복하면서 사대를 이진 탐색한다."라는 의견을 얻을 수 있었고 이해할 수 있었다.

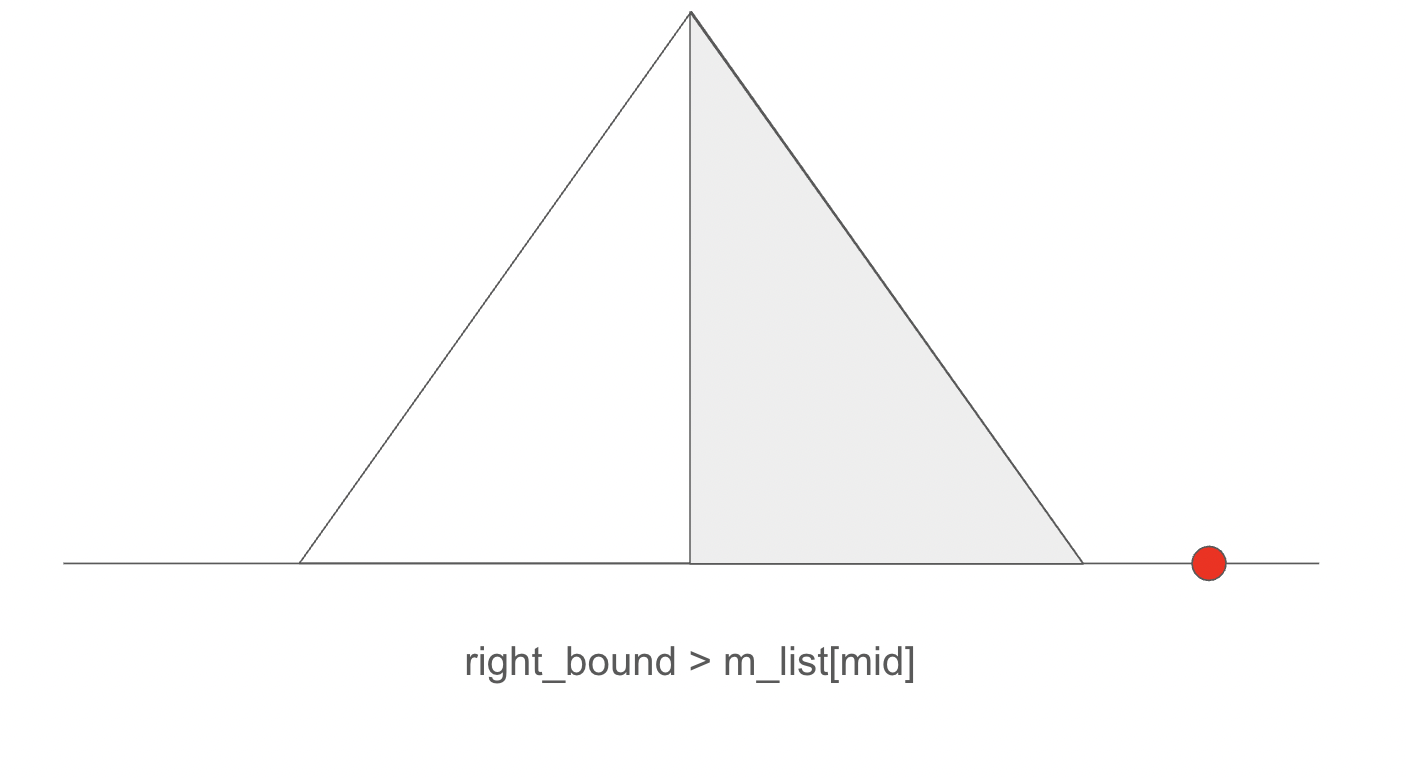
또한 이 부분 사대가 right_bound 보다 크다는 것은 사격할 수 있는 범위에서 벗어났다는 것

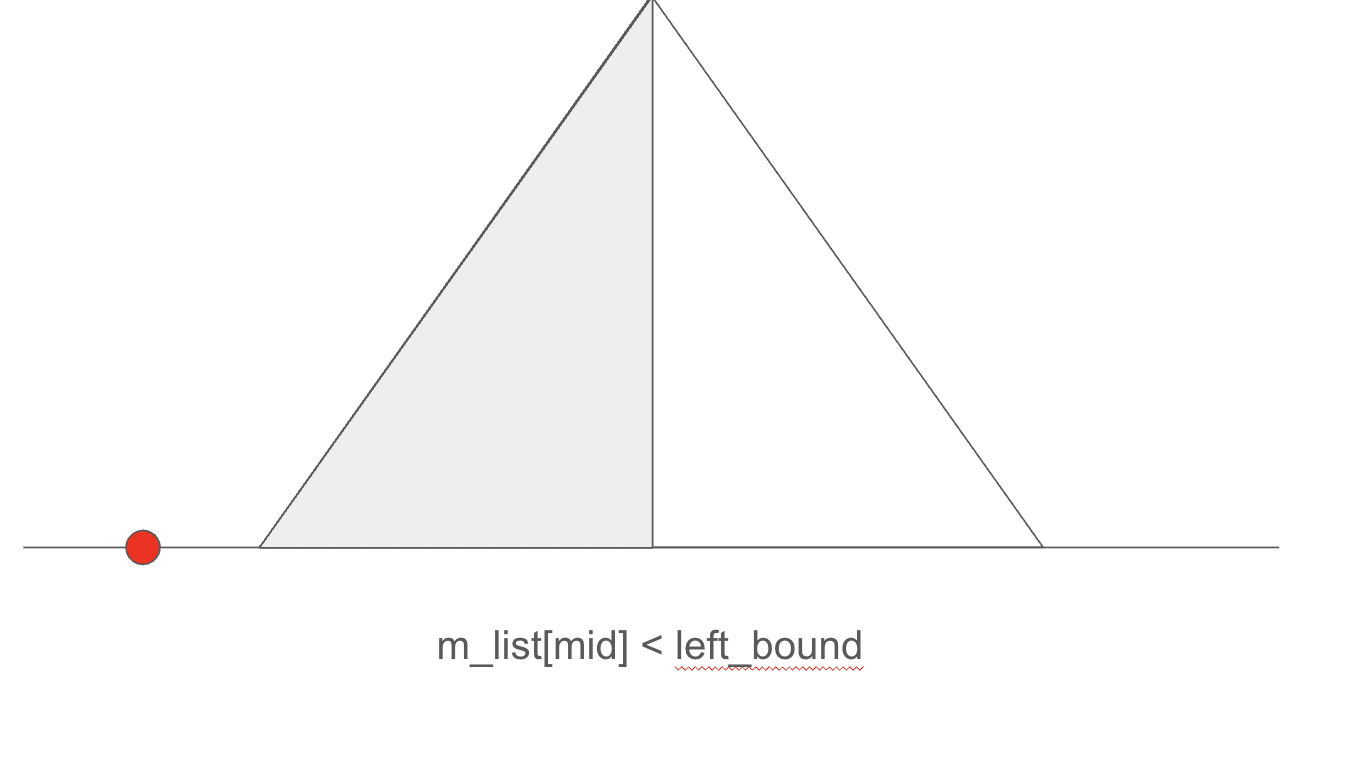
왼쪽 또한 같다.