[정글 week04] 백준 코테 동전

동전 문제는 왜이리 많은건가~~

문제

문제는 꽤나 간단하다.

T : 케이스 개수
N : 동전 종류 (오름차순)
M : 금액

N가지 동전으로 금액 M을 만드는 모든 방법의 수를 하나씩 출력

N*M으로 완전 탐색으로 문제를 해결할 수 있겠지만?
DP 활용 문제이기에, 분할 정복이 될 것만 같은 느낌 (이미 DP문제인거 암)

어찌됬든 분할하면 시간 복잡도를 줄이수 있겠다라는 느낌은 확 왔다!

"이걸 도대체 어떻게 접근하지?"라는 막막함이 있었는데 옆에서 다른 정글러들이 문제를 풀고 있길래 옆으로 달려갔지.

한참을 문제 푸는걸 구경하다가 이해를 해 버렸다.

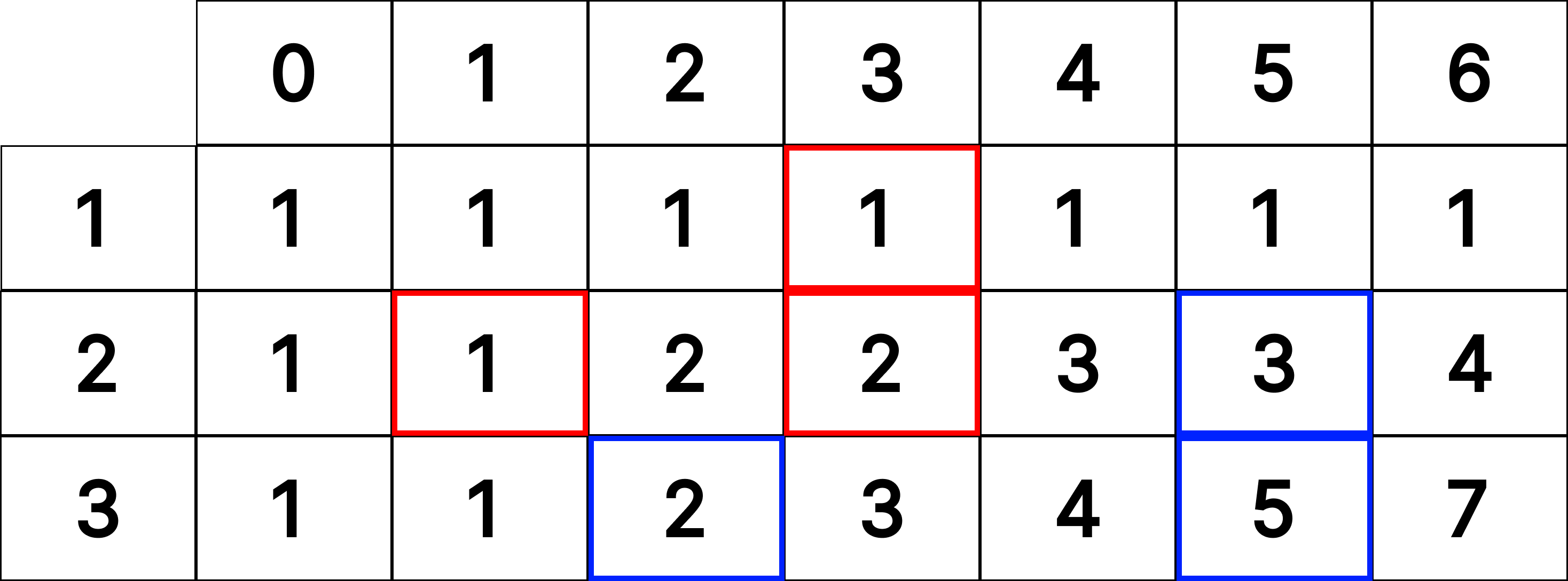
이렇게 접근이 되는건 알겠어.
보면은 [i][j]라고 했을 때
[i-1][j] + [i][j-coin] 이렇게 풀면 되겠네?

for i in range(T):
    N = int(input())
    coins = list(map(int, input().split()))
    M = int(input())

    dp = [[0] * (M+1) for _ in range(len(coins))]

    for i in range(len(coins)):
        for j in range(coins[i], M+1):
            if i == 0:
                dp[i][j] = 1
            else:
                dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]
    print(dp[-1][M])

결과는?

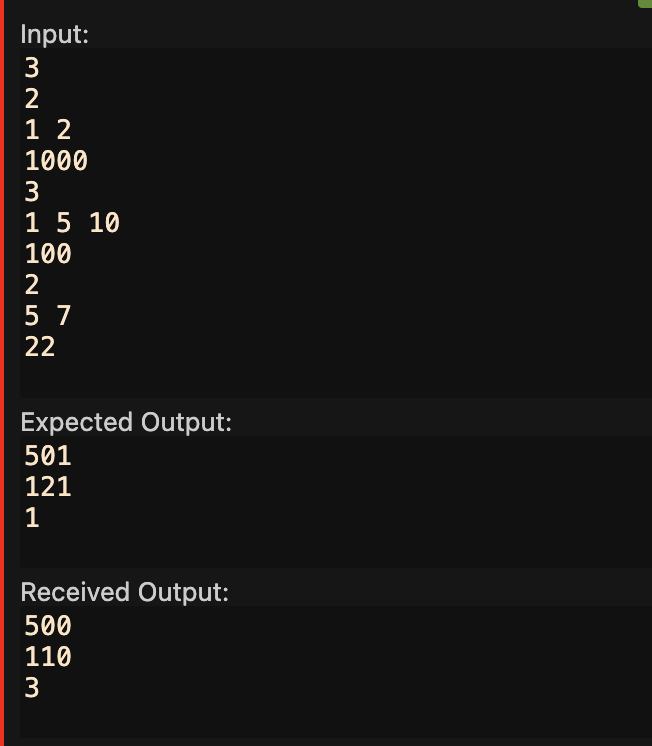
뭔가 근접한 듯 하다.

근데....뭐가 잘못된지 도저히 모르겠어서
점화식만 G(od)PT한테 부탁

사실 점화식이 아니고 코드를 보여주더라....
(어쩔 수 없다.)

for i in range(T):
    N = int(input())
    coins = list(map(int, input().split()))
    M = int(input())

    dp = [0] * (M+1)
    dp[0] = 1
    for coin in coins:
        for amount in range(coin, M+1):
            dp[amount] += dp[amount - coin]
    print(dp[M])

무엇이 다른가?
1. 1차원 배열에 M+1 배열 사용
2. dp[amount] += dp[amount - coin]

• 기존 코드 coins * M+1 사용
• 2번째 부분에 대해서는 난 이해를 아직 못함...내가 그린 그림으로는 이해가 안되는데 음....

엄청 간결해지고 공간 복잡도도 줄었다.

시간 복잡도

입력을 제외한다면 : O(N * M)

공간 복잡도

dp = O(M)

다른 것들에 공간들은 크게 무관할 듯 하다.

음 문제를 처음에 접근할 땐 너무 막막했지만,
손으로 DP 테이블을 그리고 따라 가다보니 패턴,
흐름을 읽을 수 있었고 그걸 토대로 문제에 접근할 수 있었다.

꽤나 재밌는 경험이고 잘 안풀려서 PT(G)를 받았지만 재밌었다.