📌 세그먼트 트리란?
- 세그먼트 트리는 효율적인 구간 쿼리 연산을 위해 고안된 이진 트리이다.
- 쿼리의 종류에 따라 특정 구간이 가지는 값이 달라지며 쿼리의 대표적인 예시로는 구간합, 최소, 최대 등이 있다.
📌 세그먼트 트리의 주요 연산
- 세그먼트 트리에는 두 가지 연산이 있다. 특정 구간에 대한 쿼리를 수행하는 구간 쿼리 연산과 값 변경이 일어났을 때 트리를 갱신하는 업데이트 연산이 있다.
1. 구간 쿼리
- 주어진 범위에 대해 특정 연산을 수행한 결과를 구한다.
- 대표적으로 구간합, 최대, 최소등이 있다.
2. 값 변경에 따른 업데이트
- 특정 노드의 값을 변경하면 기존 노드값과 변경된 차이를 계산하고, 이 차이만큼 구간값을 저장하고 있는 부모노드들의 값에 반영한다.
📌 세그먼트 트리의 구현
1. 세그먼트 트리의 표현
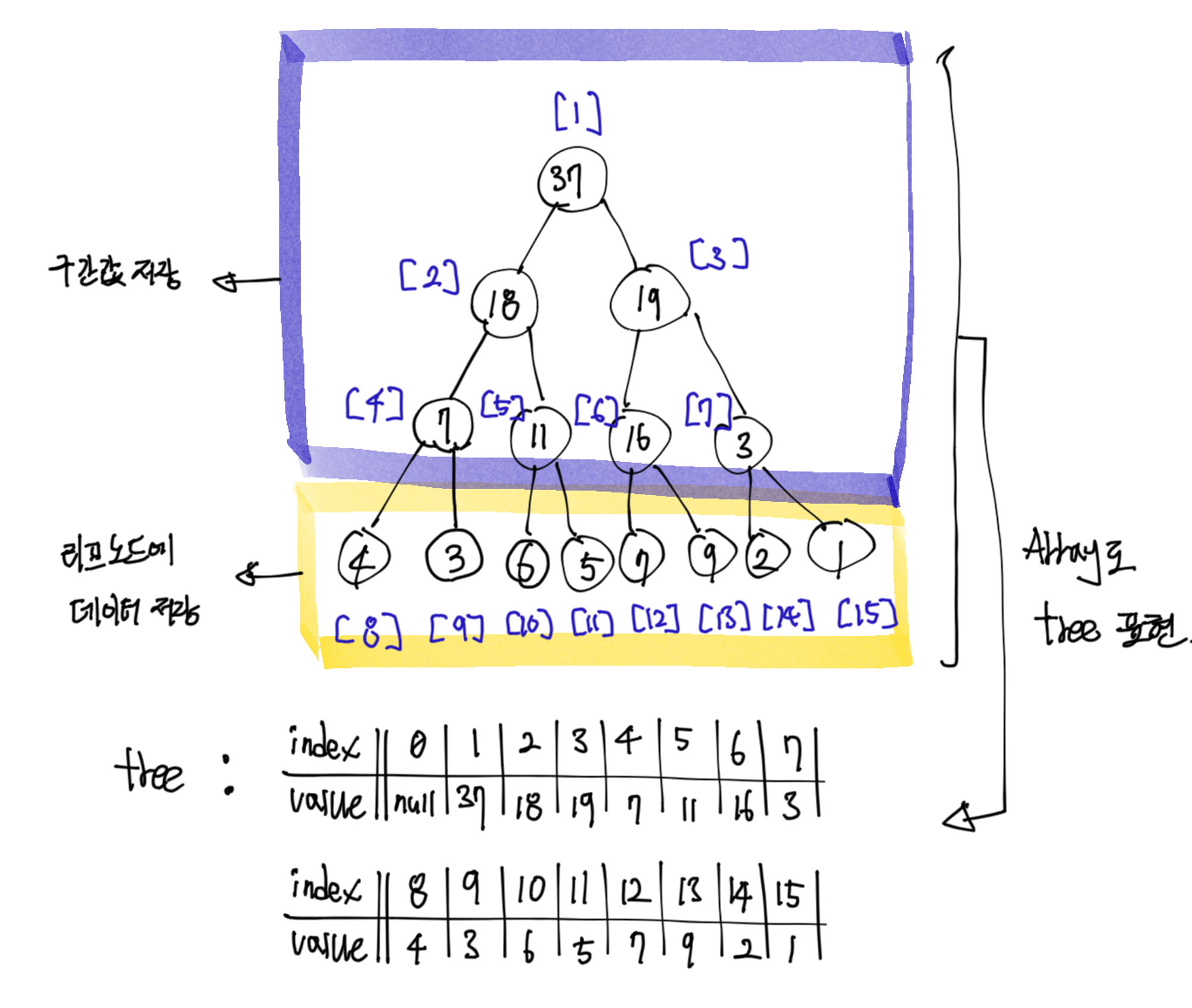
세그먼트 트리는 기본적으로 이진트리이다. 따라서 기존에 이진트리를 표현하는 방법과 동일하게 트리의 정보를 배열 형태로 저장한다. 배열의 각 인덱스에 규칙을 두어 root 노드와 노드간의 부모/자식 관계를 구분한다.
또한 세그먼트 트리는 이진트리의 리프노드에 초기 데이터를 저장하고 나머지 노드들에 구간 연산 값을 저장한다.
우선 이진 트리를 배열로 표현할 때 사용하는 인덱스에 대해 알아보자.
배열 인덱스를 통한 각 트리 노드 표현
| 노드 | 인덱스 |
|---|---|
| Root | 1 |
| Parent | Current // 2 |
| Left child | Current * 2 |
| Right child | Current * 2 + 1 |
배열의 1번 인덱스부터 사용하며 1번은 루트노드를 의미한다.
특정 노드의 부모 노드의 인덱스는 해당 노드의 인덱스에서 나누기 2를 했을 때의 몫이 부모를 뜻하게 된다.
특정 노드의 자식 노드의 인덱스는 “해당 노드 인덱스 2”가 left child를, “해당 노드 인덱스 2 + 1”이 right child를 의미하게 된다.
예를 들어 인덱스가 7인 노드의 부모 인덱스는 7//2의 몫인 3이고, 자식들의 인덱스는 72, 72 + 1 이므로 14, 15가 각각 좌측 자식, 우측 자식이 된다.
2. 세그먼트 트리 초기화
- 세그먼트 트리의 배열 크기 및 노드 배치
세그먼트 트리는 구간 쿼리를 수행할 초기 데이터 자체를 저장하는 영역과 구간 쿼리를 수행한 결과를 저장하는 영역을 분리해서 사용한다.
- 구간 쿼리를 수행하기 위한 초기 데이터는 리프노드에 저장한다.
- 구간 쿼리를 수행한 결과인 구간값들은 리프를 제외한 나머지 영역에 저장된다.
이를 저장하기 위한 배열의 크기는 초기 데이터의 수에 따라서 결정되게 되는데, 들어온 데이터가 N개라고 할 때, 트리를 저장하기 위한 배열의 크기(size)는 아래의 조건을 만족하는 크기로 잡아준다.
- size = 2^(ceiling(log2(N)) + 1)
# 위의 조건은 아래의 의미이다.
size = 2^(K+1) (단, K는 2^K >= N를 만족하는 K의 최소값)파이썬을 이용해 위를 계산해준다면 다음과 같이 구해볼 수 있다.
N = 데이터 개수
k = 0
tmp = N
# 2^K >= N를 만족하는 최소 K
while tmp != 0:
tmp //= 2
k += 1
# size = 2^(K+1)
size = pow(2, k+1)또는 파이썬의 math 라이브러리를 활용하여 더 간단하게 구할 수 있다.
N = 데이터 개수
# 2^K >= N를 만족하는 최소 K
k = math.ceil(math.log2(N))
# size = 2^(K+1)
size = pow(2, k+1)- 리프노드에 데이터 초기화 및 구간값 연산
이제 구간 연산을 수행할 데이터들을 리프노드에 순서대로 초기화해준다.
리프노드가 시작되는 인덱스는 2^K이다. 따라서 첫번째 데이터는 2^K, 두번째 데이터는 2^K + 1 … 와 같이 저장되게 된다. 즉 i 번째 데이터는 트리의 i + 2^K - 1 번 인덱스에 저장된다.
i 번째 데이터 => tree[i + 2^K - 1]예를 들어 {4, 3, 6, 5, 7, 9, 2, 1}가 데이터로 들어왔다고 했을 때, 리프노드는 다음과 같이 초기화 될 것이다.
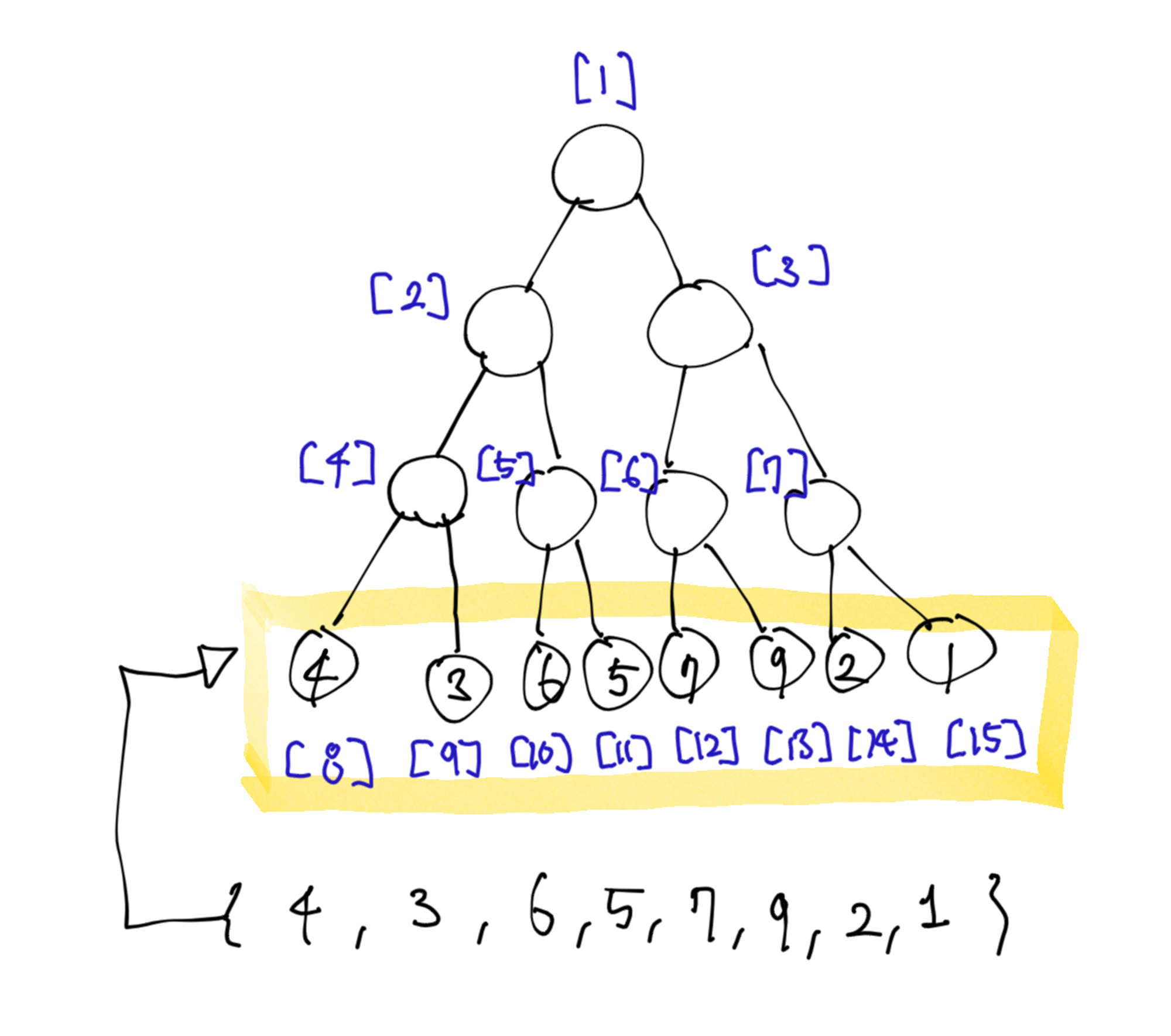
초기화 해준 리프노드들을 가지고 구간값들을 초기화한다. 이 글에서는 구간합을 구하는 연산을 예시로 작성하였다.
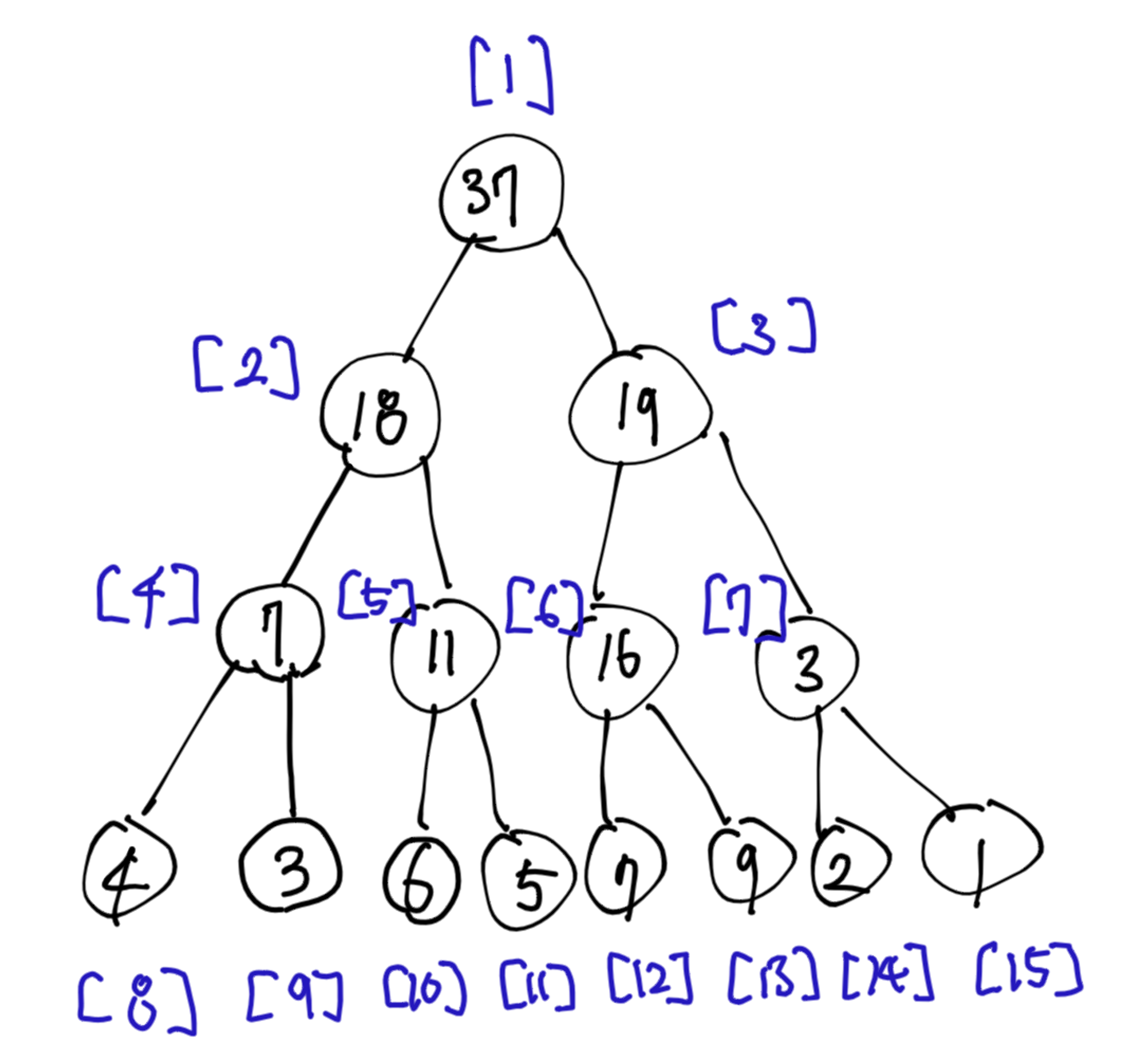
이렇게 초기화하면 리프를 제외한 트리의 각 노드들은 아래와 같이 특정 구간값을 가지게 된다.
- tree[4] : 1번째 데이터(tree[8]) ~ 2번째 데이터의 구간합(tree[9])
- tree[5] : 3번째 데이터(tree[10]) ~ 4번째 데이터의 구간합(tree[11])
- tree[2]: 1번째 데이터(tree[8]) ~ 4번째 데이터의 구간합(tree[11])
- tree[1]: 1번째 데이터(tree[8]) ~ 8번째 데이터의 구간합(tree[15]) …
따라서 만약 질의 구간이 1번째부터 4번째까지를 구하라는 것이라면 tree[2]가 해당 구간합이므로 tree[2]를 그대로 반환하면 된다.
여기까지하면 구간합이 다 구해진 것 아닌가? 하고 생각할 수도 있다.
하지만 세그먼트 트리에 연산된 특정 구간값만 가지고는 바로 반환할 수 없는 질의 구간이 들어올수도 있다.
예를 들어 1번째 데이터부터 3번째 데이터의 구간합은 세그먼트 트리의 특정 노드가 가지고 있는 값이 아니다.
1번째 데이터 ~ 2번째 데이터의 구간합인 tree[4]와 3번째 데이터인 tree[3]을 더해주면 1번째 데이터부터 3번째 데이터의 구간합을 구할 수 있다.
또 다른 예시로 2번 데이터부터 7번 데이터까지의 구간합도 세그먼트 트리에 연산되어 있는 특정 노드의 값 하나만 가지고는 반환할 수 없다.
따라서 2번 데이터의 값(tree[2]) + 3번 데이터 ~ 4번 데이터 구간합(tree[5]) + 5번 데이터 ~ 6번 데이터 구간합(tree[7]) + 7번째 데이터 값(tree[14])와 같이 추가적인 연산이 필요하다.
이렇게 질의 구간값을 구할 때 세그먼트 트리에 연산되지 구간값들에 추가적으로 다른 구간값을 더해주거나 또는 데이터를 따로 더해주어야하는 경우가 생기는데, 이를 고려하여 구현해주어야 한다.
3. 질의 구간 연산
손으로 직접 특정 질의 구간을 가정하고 질의값을 구해보자.
시작점과 끝점에서 각각 출발하여 부모노드가 질의구간 포함되는지 확인하고, 포함 여부에 따라 다음 부모로 이동하는 것을 반복하면서 질의값이 구할 것이다.
- 부모가 질의구간에 포함되는지 확인하는 기준
시작 지점과 끝 지점에 대해 각각 자신의 부모가 질의구간에 포함되려면 시작 지점의 경우 왼쪽 자식이어야 하고, 끝 지점의 경우 오른쪽 자식이어야 한다.
- 시작 지점이 왼쪽 자식이어야만 시작 지점의 부모가 질의구간에 포함된다.
- start_index % 2 == 0 이면 시작 지점의 부모는 질의구간에 포함된다.
- start_index % 2 == 1 이면 시작 지점의 부모는 질의구간에 포함되지 않는다.
- 끝 지점이 오른쪽 자식이어야만 끝 지점의 부모가 질의구간에 포함된다.
- end_index % 2 == 0 이면 끝 지점의 부모는 질의구간에 포함되지 않는다.
- end_index % 2 == 1 이면 끝 지점의 부모는 질의구간에 포함된다.
- 질의 구간에 대한 질의값을 찾아가는 과정
아래 과정을 끝 지점의 인덱스가 시작 지점의 인덱스보다 커질때까지 반복하면서 질의값을 찾아간다.
최종적으로 표시된 부분을 모두 더하면 질의값이 된다.
- 부모노드가 질의구간에 포함될 경우, 부모노드로 이동한다.
- 부모노드가 질의 구간에 포함되지 않을 경우,
- 현재 노드에 특별한 표시를 한 후 옆에 있는 부모로 이동한다.
- 이때 옆에 있는 부모란, 시작 노드의 경우 자신의 부모의 오른쪽 노드를 의미하고 끝 노드의 경우 자신의 부모의 왼쪽 노드를 의미한다.
- 질의값 구하는 과정 예시
예시를 통해 살펴보자. 다음은 2번째 ~ 5번째 데이터의 구간합이 질의 구간으로 제시된 예시이다.
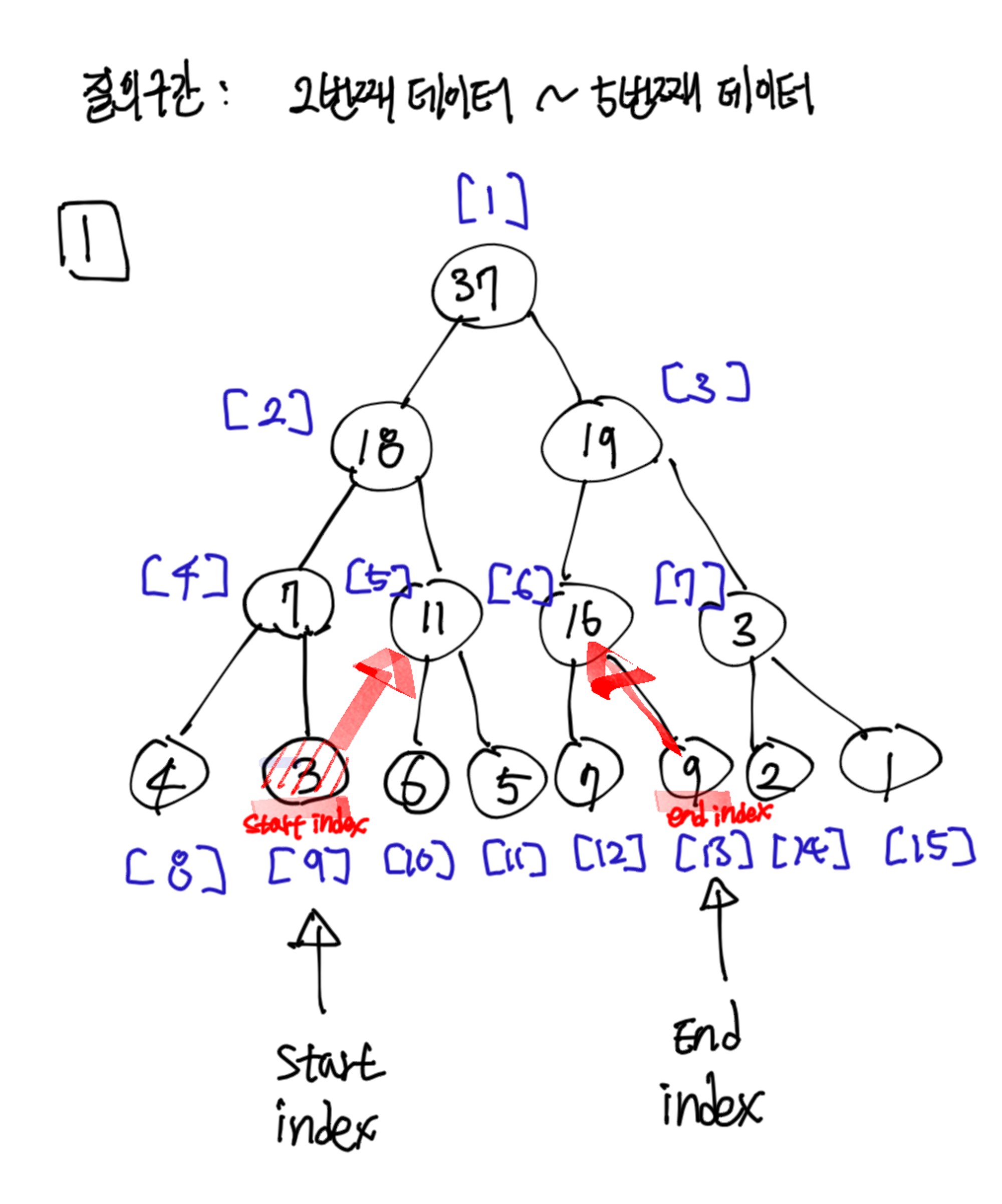
우선 시작지점인 2번째 데이터에 해당하는 9번 인덱스 노드와, 끝 지점인 5번째 데이터에 해당하는 13번 인덱스로부터 시작한다.
우선 시작 인덱스와 끝 인덱스에 대해서 해당 부모가 질의 구간에 속하는지 확인한다.
시작 지점 인덱스 % 2 = 1 이므로 해당 노드는 right child 이고 이에 따라 해당 부모인 tree[4]는 질의구간에 포함되지 않는다는 것을 알 수 있다.
왜냐하면, tree[4]는 1번~2번 데이터의 구간합인데 시작점은 2번부터이기 때문에 이 구간값은 사용할 수 없다.
즉 시작점을 기준으로 했을 때는 해당 노드가 왼쪽 자식이어야만 부모가 질의 구간에 포함되게 된다.
따라서 현재 시작 지점이 위치한 노드(tree[9])에 특별한 표시를 하고 자신의 부모의 오른쪽 노드로 이동한다.
마지막에 표시가 되어있는 부분들을 더해주어 질의값이 구해지게 된다.
이제 끝 지점인 6번째 데이터에 해당하는 tree[13]을 살펴보면 13 % 2 = 1 이므로
해당 부모가 질의구간에 포함되는 것을 알 수 있다.
끝 지점에서 봤을 때는 해당 노드가 오른쪽 자식이어야만 자신의 부모가 질의구간에 포함되기 때문이다.
부모가 질의구간에 포함되므로 별도의 표시없이 자신의 부모(tree[6])으로 이동한다.

start_index가 11로 이동하고 end_index가 16으로 이동한 후에도 동일한 과정을 반복한다.
start_index % 2 = 1 이므로 해당 부모가 질의구간에 포함되지 않는다. 따라서 부모의 오른쪽 노드(tree[3])로 이동한다.
end_index % 2 = 0 이므로 끝 지점의 부모는 질의구간에 포함된다. 따라서 부모인 tree[2]로 이동한다.
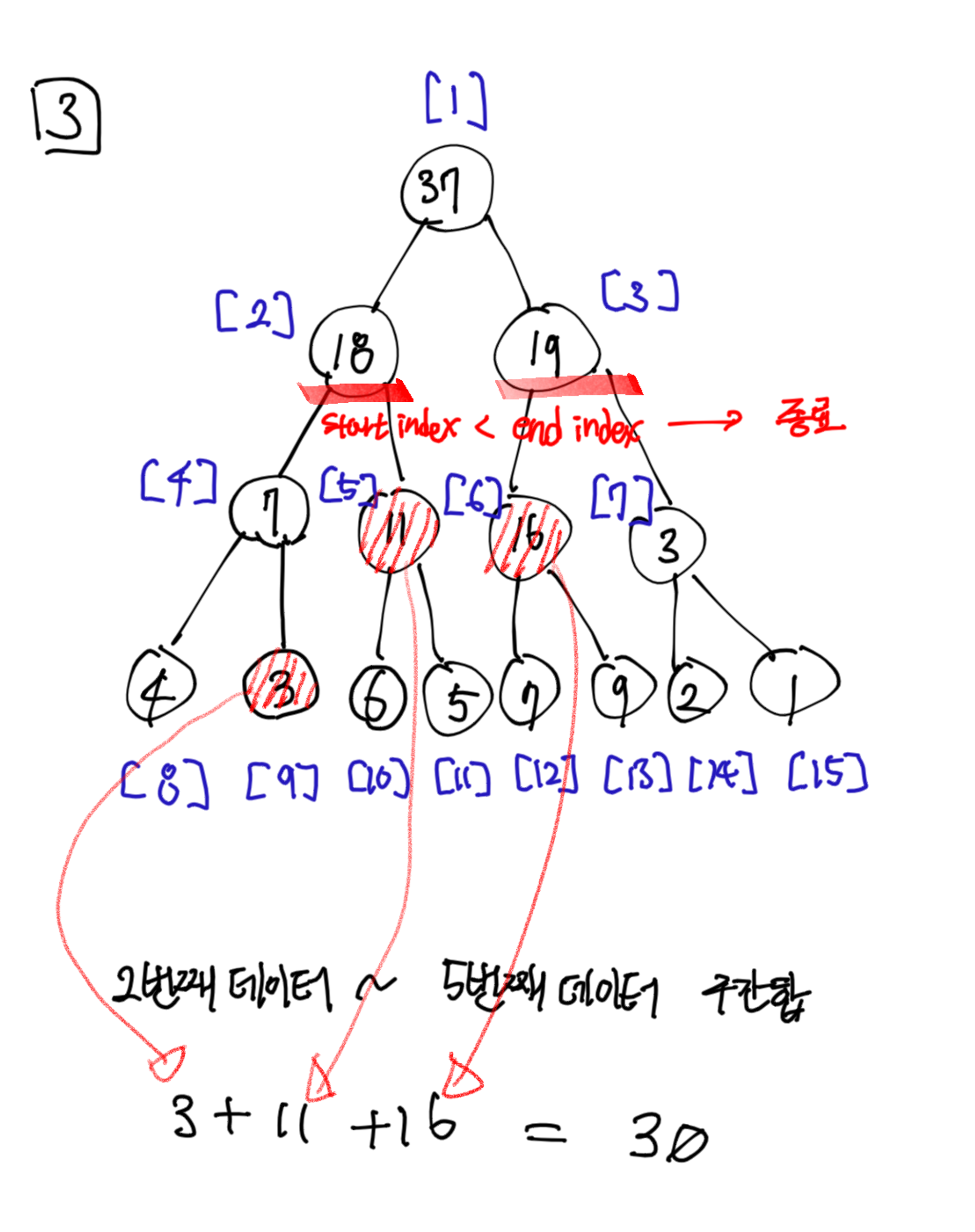
start_index와 end_index가 엇갈렸으므로(start_index < end_index) 종료한다.
최종적으로 표시한 부분을 다 더하면 질의 구간에 대한 구간합이 된다.
