소수
- 자신 보다 작은 두개의 자연수를 곱하여 만들 수 없는 1보다 큰 자연수
- 1과 자기 자신만을 약수로 갖는 수
- 1과 자신으로만 나누어 지는 수
- ex) 2, 3, 5, 7…
에라토스테네스의 체
-
알고리즘
-
2부터 구하구자 하는 모든 수 나열
-
2는 소수이므로 오른쪽에 2쓴다.
-
자신을 제외한 2의 배수 모두 지운다.
-
남은 수 가운데 3은 소수이므로 오른쪽에 쓴다.
-
자신을 제외한 3의 배수 모두 지운다.
-
남은 수 가운데 5은 소수이므로 오른쪽에 쓴다.
-
자신을 제외한 5의 배수 모두 지운다.
-
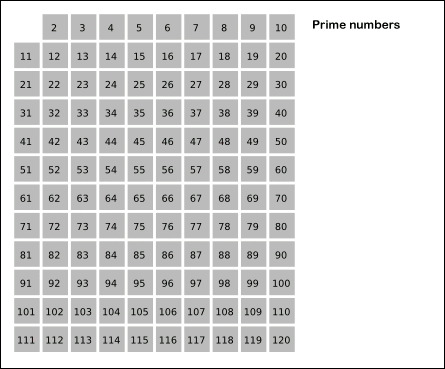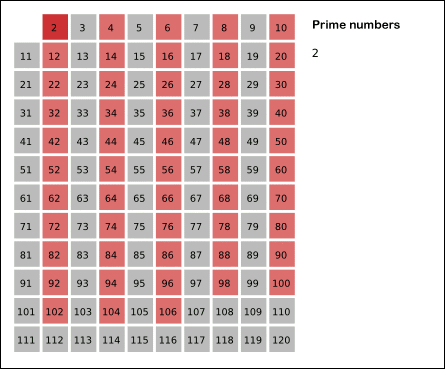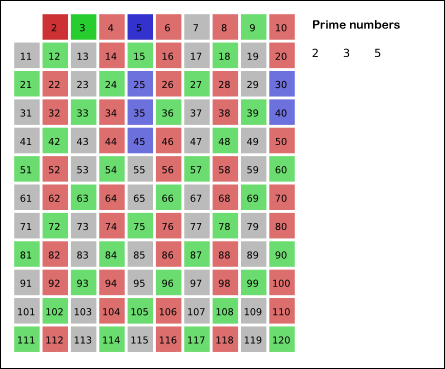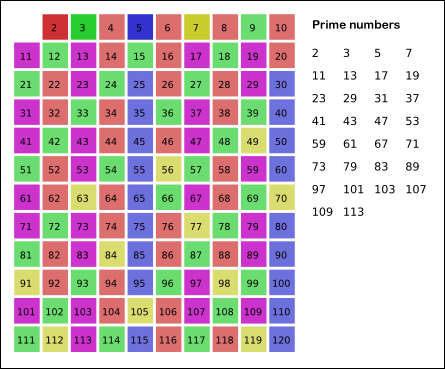
남은 수 가운데 7은 소수이므로 오른쪽에 쓴다.
-
자신을 제외한 7의 배수 모두 지운다.
-
위의 과정 반복하면 구하는 구간의 모든 소수가 남는다.
-
-
위 그림의 경우, 11^2 > 120이므로 11보다 작은 수의 배수들만 지워도 충분한다. 즉 120보다 작거나 같은 수 가운데 2, 3, 4, 5의 배수를 지우고 남는 수는 모두 소수이다.
- 알고리즘 요약
- 1보다 큰 모든 자연수는 소수의 곱으로 이루워졌다.
- 자연수 n이 √n보다 작은 소수들로 나눠떨어지지 않으면 자연수 n은 소수이다.
JS로 에라토스테네스의 체 구현
function solution(n) {
// idx 0, 1은 false / 나머지는 true인 길이가 n(idx : 0 ~ n)인 배열 생성
let arr = Array(n + 1).fill(true).fill(false, 0, 2)
// i : n의 제곱근까지 loop
for (let i = 2; i <= Math.sqrt(n); i++) {
if (arr[i]) {
// i의 배수 false로 변경
for (let j = i * i; j <= n; j += i) {
arr[j] = false;
}
}
}
return arr
}- 소수개수 및 소수 반환하기
let isPrime = solution(120)
// 소수 개수 구하기
let countPrime = isPrime.filter(e => e).length // 30
// 소수 구하기
let prime = isPrime.map((v, i) => v ? i : 0).filter(e => e)
// [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113