문제 설명
현대모비스에서 전기차로 경사로 주행 테스트를 하려고 합니다. 경사로 테스트는 n×m 크기의 격자 형태의 공간에서 진행되며, 각 칸에 적힌 숫자는 높이를 나타냅니다. 전기차는 격자 내의 모든 칸에서 출발 가능하며, 상하좌우로 인접한 칸으로만 이동 가능하고 격자 밖을 벗어날 수는 없습니다. 전기차가 인접한 칸으로 이동하는 길의 경사는 이동하려는 칸의 높이에서 현재 칸의 높이를 뺀 값입니다. 예를 들어 높이가 5인 칸에서 7인 칸으로 이동하는 길의 경사는 2(= 7 - 5)이고, 높이가 6인 칸에서 높이가 1인 칸으로 이동하는 길의 경사는 -5(= 1 - 6)입니다.
경사 수열 d가 주어집니다. 경사 수열은 테스트에서 전기차가 이동할 길의 경사를 나타내며, d[i]는 전기차가 i+1번째로 이동할 때 경사가 d[i]인 길을 지나야 함을 나타냅니다. 전기차가 경사로를 반복적으로 이동할 때 받는 스트레스를 관찰하기 위해 주어진 경사수열을 k번 반복할 수 있는 경로를 찾으려 합니다. 같은 칸을 여러 번 방문하거나 지나온 길을 바로 되돌아가는 경로도 가능합니다.
격자 칸의 높이를 담은 2차원 정수 배열 grid, 경사 수열을 담은 1차원 정수 배열 d와 경사 수열을 반복하는 횟수를 나타내는 정수 k가 매개변수로 주어집니다. 이때, 격자 내에서 조건을 만족하는 경로의 수를 return 하도록 solution 함수를 완성해 주세요. 단, 답이 커질 수 있으므로 1,000,000,007로 나눈 나머지를 return 해주세요.
https://school.programmers.co.kr/learn/courses/30/lessons/214290
제한사항
- 3 ≤
grid의 길이 =n≤ 8 - 3 ≤
grid[i]의 길이 =m≤ 8- 0 ≤
grid[i][j]≤ 1,000 grid[i][j]는 각자의i+1번째 행,j+1번째 열에 위치한 칸의 높이를 나타냅니다.
- 0 ≤
- 1 ≤
d의 길이 ≤ 100- -100 ≤
d의 원소 ≤ 100
- -100 ≤
- 1 ≤
k≤ 109
입출력 예
| grid | d | k | result |
|---|---|---|---|
| [[3, 4, 6, 5, 3], [3, 5, 5, 3, 6], [5, 6, 4, 3, 6], [7, 4, 3, 5, 0]] | [1, -2, -1, 0, 2] | 2 | 16 |
| [[3, 6, 11, 12], [4, 8, 15, 10], [2, 7, 0, 16]] | [1, -2, 5] | 3 | 1 |
| [[0, 0, 0], [1, 0, 0], [0, 0, 0], [0, 0, 1], [1, 0, 0]] | [0, 0, 1, -1, 0, 0, 1, -1] | 10 | 595737277 |
풀이
저한텐 넘모 어려웠습니다...
문제는 크게 조건에 맞는 경로 찾기와 이를 k번 반복하는 경우의 수 구하기, 두 부분으로 나뉜다.
1. 조건에 맞는 경로 찾기
DP를 사용해 grid에서 d의 경사를 이루는 경로를 찾는다.
int n =grid.length;
int m = grid[0].length;
int dl = d.length;
//dp[순서][출발칸][목적지칸]
long dp[][][] = new long[dl+1][n*m][n*m];
for(int i = 0; i < n*m; i++){
dp[0][i][i] = 1;
}
for(int l = 1; l <= dl; l++){
for(int i = 0; i < n*m; i++){
int x = i % m;
int y = i / m;
for(int dir = 0; dir < 4; dir++){
int nx = x + dx[dir];
int ny = y + dy[dir];
if(nx < 0 || nx >= m || ny < 0 || ny >= n || grid[ny][nx] - grid[y][x] != d[l-1] ){
continue;
}
for(int j = 0; j < n*m; j++){
dp[l][j][ny*m + nx] += dp[l-1][j][i] % MOD;
dp[l][j][ny*m + nx] %= MOD;
}
}
}
}배열 dp[순서][출발칸][도착칸]에 출발칸에서 d[0]~d[순서] 의 경사를 통과해 도착칸에 도달할 수 있는 경로의 수를 저장한다.
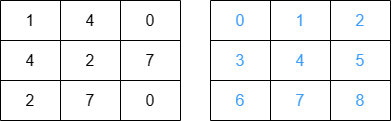
예시를 보자. 왼쪽 그림에서 숫자는 그 칸의 높이이고 오른쪽 그림에서 숫자는 해당 칸의 번호이다.
경사가 d = [3,-2,5]이라고 하면 칸0에서 칸1, 칸3으로 갈 때 경사가 3 = d[0]이므로 dp[순서 = 1][출발칸 = 0][도착칸 = 1] = dp[1][0][3] = 1이다.
칸1이나 칸3에서 칸4로 갈 때 경사는 -2 = d[1]이므로 d[2][0][4] = d[1][0][1] + d[1][0][3] = 2이다. 칸3에서 칸6으로도 갈 수 있으므로 d[2][0][6] = 1이다.
칸4와 칸6에서 칸7로 갈 때 경사는 5 = d[2]이므로 dp[3][0][7] = d[2][0][6] + d[2][0][4] = 1 + 2 = 3이다. 즉 칸0에서 경사 3,-2,5를 거쳐 칸7에 도달할 수 있는 경로의 개수는 3개이다.
2. k번 반복하는 경우의 수 구하기
위 과정을 거치면 grid에 있는 모든 칸 A,B에 대해 A에서 시작해서 B에 도착하는 경로의 수를 모두 구할 수 있을 것이다.
1) 그래프로 표현
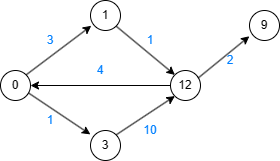
이 예시를 보자. 그래프의 파랑색 숫자는 경로의 수로, 칸0에서 칸1로 가는 경로는 3개이다.
경로를 한 번 거쳐 칸1에 도착하는 경우의 수는 칸0에서 출발하는 3개의 경우고, 칸0에 도착하는 경우의 수는 칸12에서 오는 4개의 경우다.
경로를 두 번 거쳐 칸1에 도착하는 경우의 수는 칸12에서 칸0을 거쳐 오는 경로로, 4 x 3 = 12이다.
여기서 경로를 X번 거쳐 칸1에 도착하는 경우의 수는 경로를 X-1번 거쳐 칸0에 도착하는 경우의 수 x 3( 칸0 -> 칸1 경로의 수) 임을 알 수 있다.
k가 작을 경우 이를 반복해서 정답을 구할 수 있지만 k의 최댓값이 10억이므로 힘들다.
2) 행렬로 표현
대신 이를 행렬로 표현해보자.
행렬의 (i행,j열) 성분이 칸i에서 시작해 칸j에 도착하는 경로의 수인 행렬A를 만든다. 사실 따로 만들 필요없이 dp[경사의 수]를 사용하면 된다.
이 행렬A를 k번 거듭제곱한 행렬Ak의 (i, j)성분에는 칸i에서 시작해 경사를 k번 거쳐 칸j에 도착하는 경우의 수가 저장된다.
//행렬의 곱을 구하기 위한 함수
static long[][] mulMatrix(long[][] a, long[][] b){
int n = a.length;
long[][] result = new long[n][n];
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
for(int l = 0; l < n; l++){
result[i][j] += ((a[i][l] % MOD) * (b[l][j] % MOD))% MOD;
}
}
}
return result;
}문제는 k가 너무 크므로 k번 반복할 수 없으니 다른 방법을 써야 된다.
3)행렬 제곱하기
행렬A를 제곱하면 A2가 되고 이를 다시 제곱하면 A4가 된다.
이런식으로 Ak를 구하기 위해 필요한 계산의 횟수를 약 log2k정도로 줄일 수 있으므로 이 방법으로 A의 거듭제곱을 구한다.
int count = 0;
while(Math.pow(2, count) < k ){
count++;
}
long edgePower[][][] = new long[count+1][n*m][n*m];
//dl = d.length
edgePower[0] = dp[dl];
for(int c = 1; c <= count ; c++){
edgePower[c] = mulMatrix(edgePower[c-1], edgePower[c-1]);
}남은 건 A의 거듭제곱으로 Ak를 구하면 된다.
//시작은 단위행렬로
long mat[][] = new long[n*m][n*m];
for(int i =0; i < n*m; i++){
mat[i][i] = 1;
}
int kNum = k;
while(kNum > 0){
if(kNum >= Math.pow(2, count)){
mat = mulMatrix(mat, edgePower[count]);
kNum -= Math.pow(2, count);
}
count --;
} k를 이진법으로 표현한다고 생각하면 이해가 쉽다.
구하고자 하는 답인 k번 경사를 반복할 수 있는 경우의 수는 Ak 원소의 합이다.
코드
import java.util.*;
class Solution {
static int MOD = 1000000007;
static int dx[] = {1,0,-1,0};
static int dy[] = {0,1,0,-1};
public int solution(int[][] grid, int[] d, int k) {
int n =grid.length;
int m = grid[0].length;
int dl = d.length;
//dp[순서][출발칸][목적지칸]
long dp[][][] = new long[dl+1][n*m][n*m];
for(int i = 0; i < n*m; i++){
dp[0][i][i] = 1;
}
for(int l = 1; l <= dl; l++){
for(int i = 0; i < n*m; i++){
int x = i % m;
int y = i / m;
for(int dir = 0; dir < 4; dir++){
int nx = x + dx[dir];
int ny = y + dy[dir];
if(nx < 0 || nx >= m || ny < 0 || ny >= n || grid[ny][nx] - grid[y][x] != d[l-1] ){
continue;
}
for(int j = 0; j < n*m; j++){
dp[l][j][ny*m + nx] += dp[l-1][j][i] % MOD;
dp[l][j][ny*m + nx] %= MOD;
}
}
}
}
int count = 0;
while(Math.pow(2, count) < k ){
count++;
}
long edgePower[][][] = new long[count+1][n*m][n*m];
edgePower[0] = dp[dl];
for(int c = 1; c <= count ; c++){
edgePower[c] = mulMatrix(edgePower[c-1], edgePower[c-1]);
}
long mat[][] = new long[n*m][n*m];
for(int i =0; i < n*m; i++){
mat[i][i] = 1;
}
int kNum = k;
while(kNum > 0){
if(kNum >= Math.pow(2, count)){
mat = mulMatrix(mat, edgePower[count]);
kNum -= Math.pow(2, count);
}
count --;
}
long answer = 0;
for(int i = 0; i <n*m; i++){
for(int j = 0; j < n*m; j++){
answer += mat[i][j];
answer %= MOD;
}
}
return (int)answer;
}
static long[][] mulMatrix(long[][] a, long[][] b){
int n = a.length;
long[][] result = new long[n][n];
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
for(int l = 0; l < n; l++){
result[i][j] += ((a[i][l] % MOD) * (b[l][j] % MOD))% MOD;
}
}
}
return result;
}
}후기 : 다시 제 글을 읽어보니 형편없지만 그래프같은 걸 그리는 게 생각보다 많이많이 귀찮다는 걸 알게 됐습니다..
6개의 댓글
좋은 해설 잘 보았습니다!
혹시 아직 코린이라 그런데,
//dp[순서][출발칸][목적지칸]
long dp[][][] = new long[dl+1][n*m][n*m];
이 부분에서 왜 n*m으로 하는지 알 수 있을까요?
new long[dl+1][grid.length][grid[0].length] 가 아닌 이유용ㅠㅜ
좋은 글 다시 한번 감사합니다!
mulMatrix() 의 변수가 지문에서의 k(d의 반복 횟수)와 같아보여 혼란이 오는 것 같습니다.
mulMatrix()의 k는 0 ~ grid의 원소 개수이므로 다른 변수 이름으로 하면 혼동이 없을 것 같습니다.
공감하며 읽었습니다. 좋은 글 감사드립니다.