Kruskal Algorithm(최소 신장 트리 | MST)

예제 : 최소 스패닝 트리

크루스칼 알고리즘은 그래프가 주어졌을 때 그래프의 모든 정점을 연결하는 가장 작은 비용의 트리(MST)를 구현하는 알고리즘이다.

크루스칼 알고리즘은 가중치가 최소인 정점부터 MST에 포함시키기 때문에 그리디한 방식이라고 말할 수 있다.

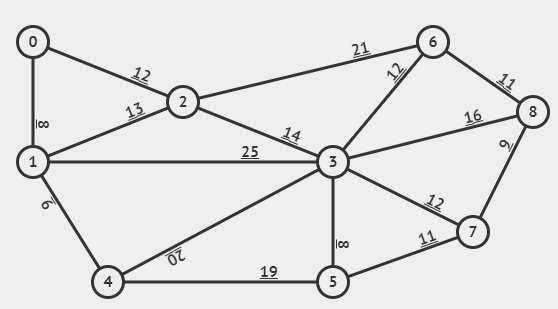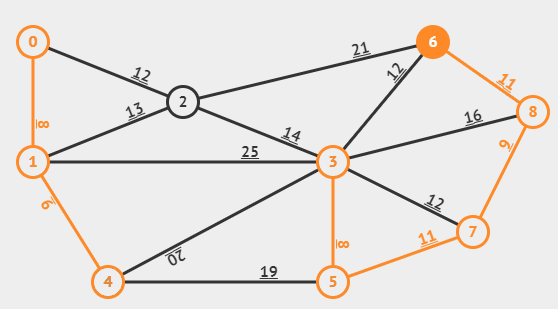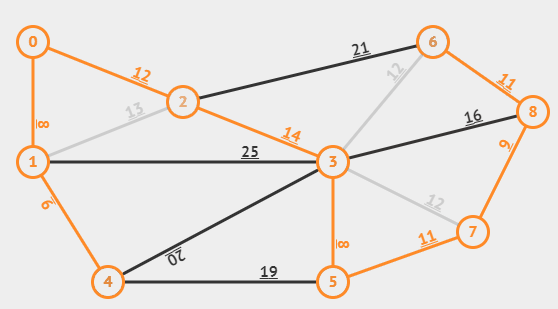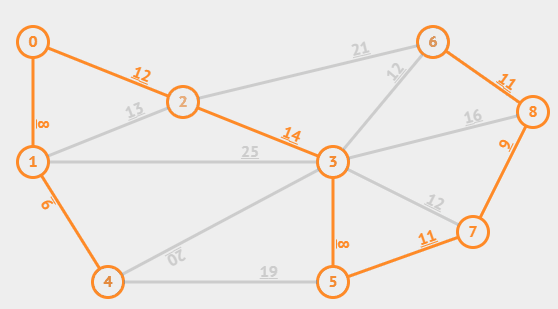
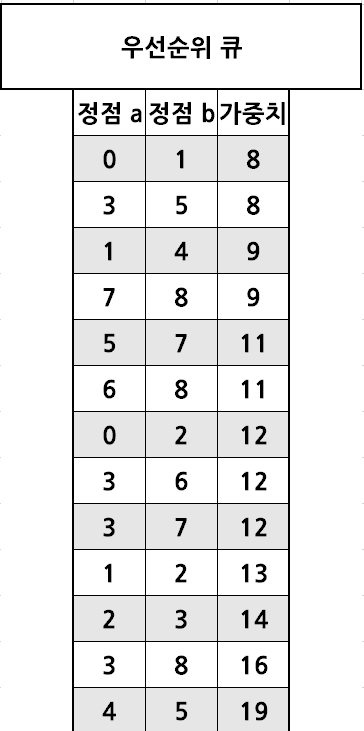
위 그림을 바탕으로 크루스칼 알고리즘을 이해해보자.

가장 먼저 MST에 추가된 간선은 0번 정점과 1번 정점을 잇고 있는 가중치가 8인 간선이다.

그 이후 3번 정점과 5번 정점을 잇고 있는 가중치가 8인 간선도 MST에 포함 되었다.

이를 구현하기 위해 우선 간선들을 가장 작은 순서대로 저장해 둘 공간이 필요하다. 이를 priority_queue를 이용하여 구현한다.

우선순위 큐에는 간선이 잇고 있는 정점과 가중치에 대한 정보가 모두 들어가야 하므로 구조체를 이용하자.

#include <bits/stdc++.h>

using namespace std;

struct Data
{
	int		node_a;
	int		node_b;
	int		weight;
	bool operator<(const Data d) const
	{
		return weight > d.weight;
	}
    // 우선순위 큐의 정렬 방식을 결정한다. 
    연산자 오버로딩을 이용하여 가중치가 작은 Data들이 우선순위 큐의 Top으로 위치하게 만든다.
};

Data	make_data(int a, int b, int c)
{
	Data	ret;
	
	ret.node_a = a;
	ret.node_b = b;
	ret.weight = c;
	return (ret);
}

priority_queue<Data>	pq;

이를 이용해 간선의 정보를 입력받으면 아래와 같은 형태로 간선을 저장할 수 있다.

MST는 트리이기 때문에 Cycle이 발생하면 안된다. 즉, 이를 판단하기 위한 로직이 추가로 필요하다.

Union Find 알고리즘

Cycle이 발생하였는지에 대한 여부는 Union Find 알고리즘을 이용하여 쉽게 파악할 수 있다.

만약 두 정점에 Find 함수를 사용하였을 때 그 결과가 같다면, 이미 두 정점은 서로 이어져있다고 말할 수 있다.

그렇다면 두 정점을 다시 잇는 것은 Cycle을 만드는 것과 동일한 의미이므로, 이를 이용하여 MST에 간선을 추가할지 간선을 포기할지 결정하면 된다.

int		arr[10001];

int		find(int a)
{
	if (arr[a] == a)
		return (a);
	return (arr[a] = find(arr[a]));
}

void	uni(int a, int b)
{
	a = find(a);
	b = find(b);
	if (a == b)
		return ;
	arr[a] = b;
}

int		is_loop(int a, int b)
{
	return (find(a) == find(b));
}

위와 같이 Union Find 알고리즘을 구현한 뒤

while (!pq.empty())
{
	node_a = pq.top().node_a;
	node_b = pq.top().node_b;
	weight = pq.top().weight;
    pq.pop();
	if (!is_loop(node_a, node_b)) // 만약 node_a 와 node_b가 이미 연결되어 있지 않다면?
	{
		uni(node_a, node_b); // node_a와 node_b를 union 해준다.
		ans += weight;
	}
}

위에서 설명한 그대로 코드를 구현하면 MST를 구할 수 있다.