딥러닝
인간의 뇌는 뉴런이라는 세포로 이루어져 있습니다. 각 뉴런은 시냅스로 연결되는데, 자극이 특정 임계치를 넘어가면 다른 뉴런에 전달하고, 임계치를 넘기지 못하면 전달하지 않습니다. 이와 같은 뇌의 신경망 아이디어를 머신러닝에 도입한 것을 인공신경망(Aritificial Neural Network)라고 합니다. 신경망을 기반으로 학습하는 방법을 딥러닝(Deep learning)이라고 합니다.
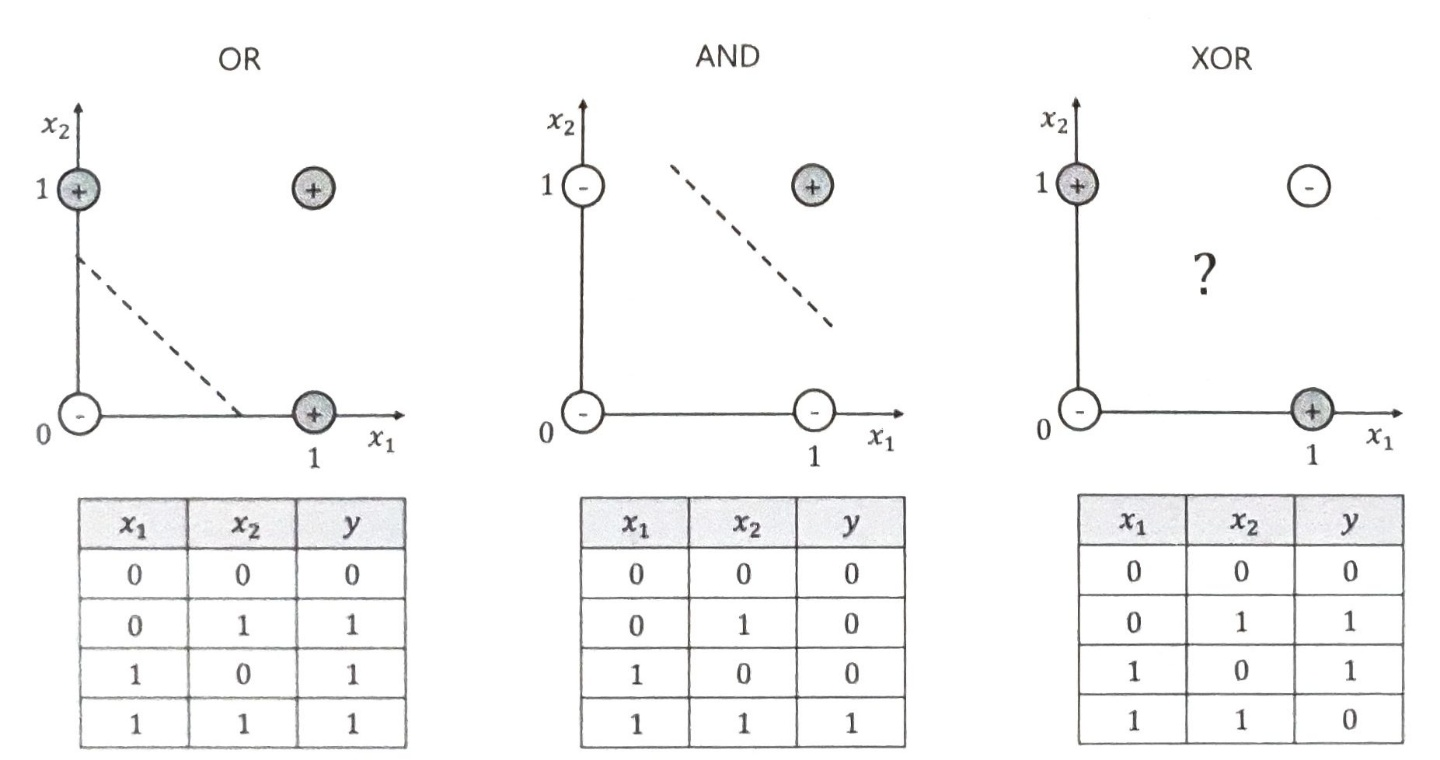
초기 딥러닝은 XOR문제로 이야기가 시작됩니다. 위의 그림에서 선 하나로 xor을 구분하려면 어떻게 해야 할까요? 기하학적으로 기존 데이터의 공간을 변형시켜 하나의 직선으로 두 종류의 데이터를 구분해 낼 수 있습니다.
평평한 종이를 구부려서 직선을 긋고 다시 종이를 펼치는 것 처럼 공간을 변형시킬 수 있습니다.
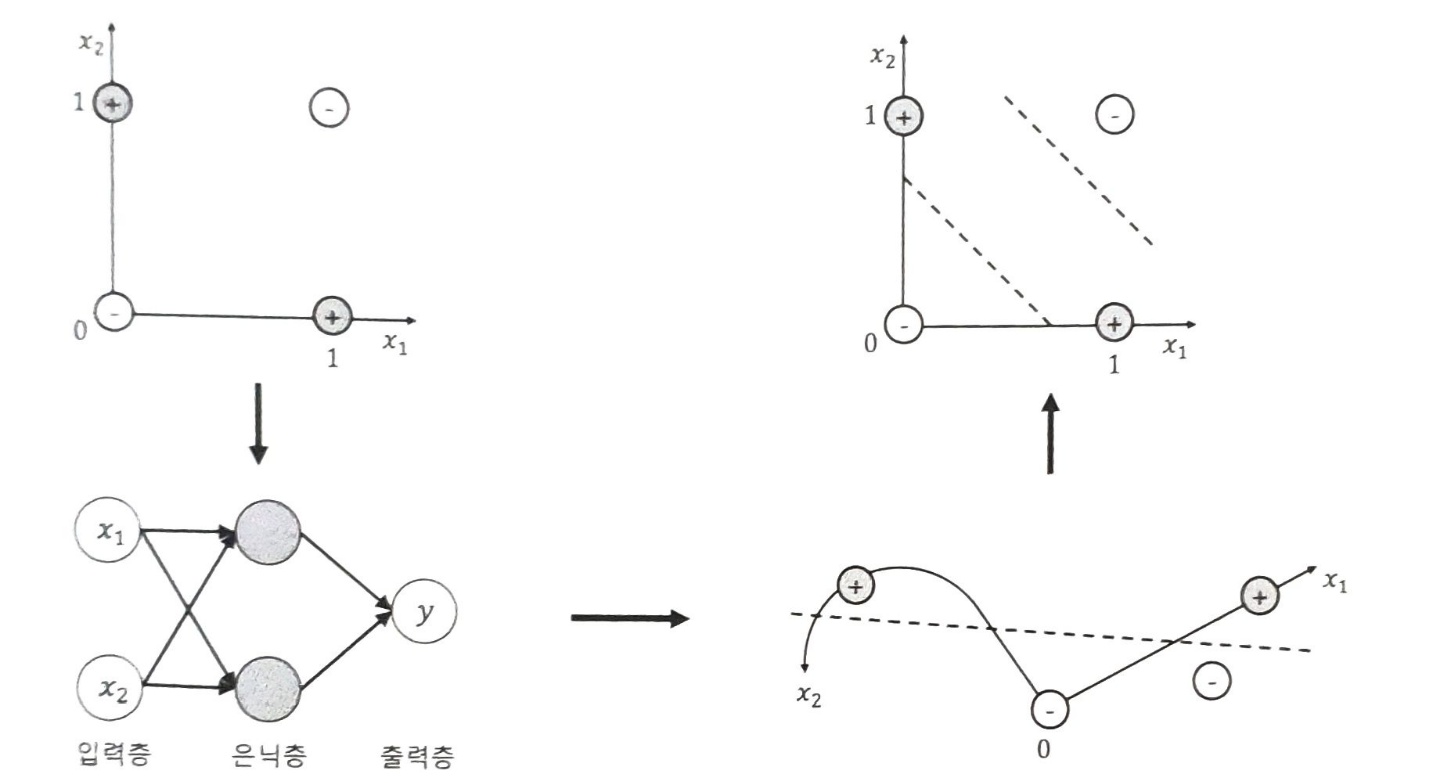
퍼셉트론
퍼셉트론은 두 개의 입력이 있을 때 하나의 뉴런으로 두 개의 입력을 계산하고, 출력값을 계산하는 모델입니다.
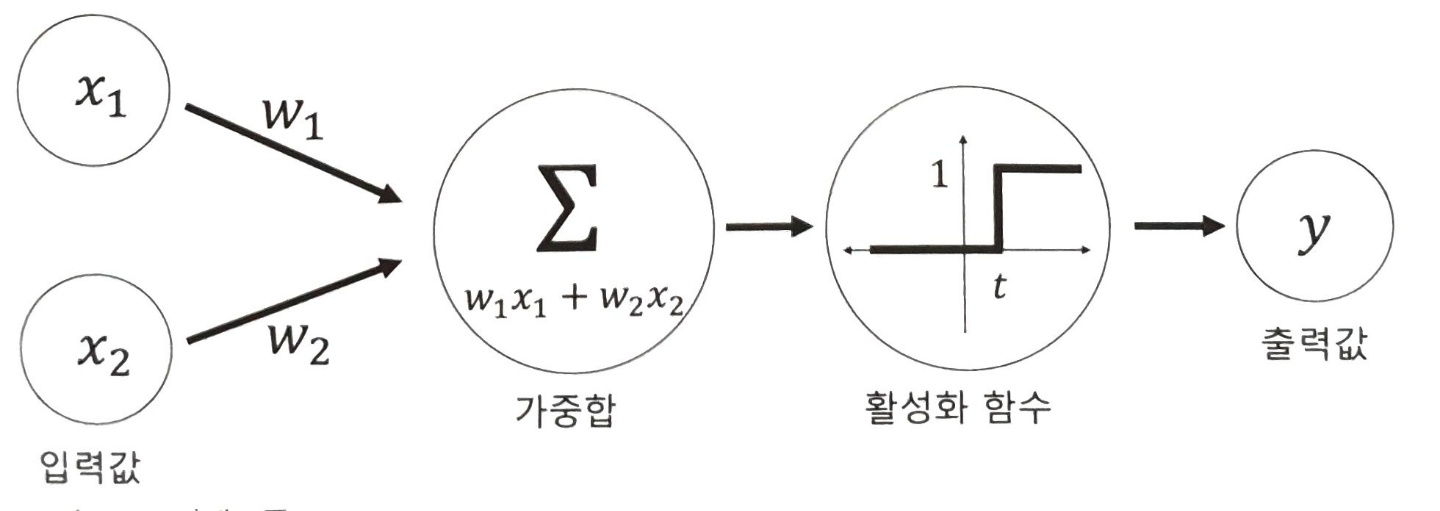
위의 그림에서 동그라미는 노드를 의미하고, 노드는 뉴런에 해당합니다. x1, x2등 입력 데이터에 가중치(w1, w2)를 곱한 후 더한 값을 가중합이라고 합니다. 이 가중합을 활성화 함수(activation function)를 통해 최종 출력값을 반환합니다.
활성화 함수
오늘날의 뉴런은 활성화 함수로 다양한 비선형 함수를 사용합니다.
비선형 활성화 함수에는 시그모이드 함수, 렐루함수, 하이퍼볼릭 탄젠트 함수가 있습니다.
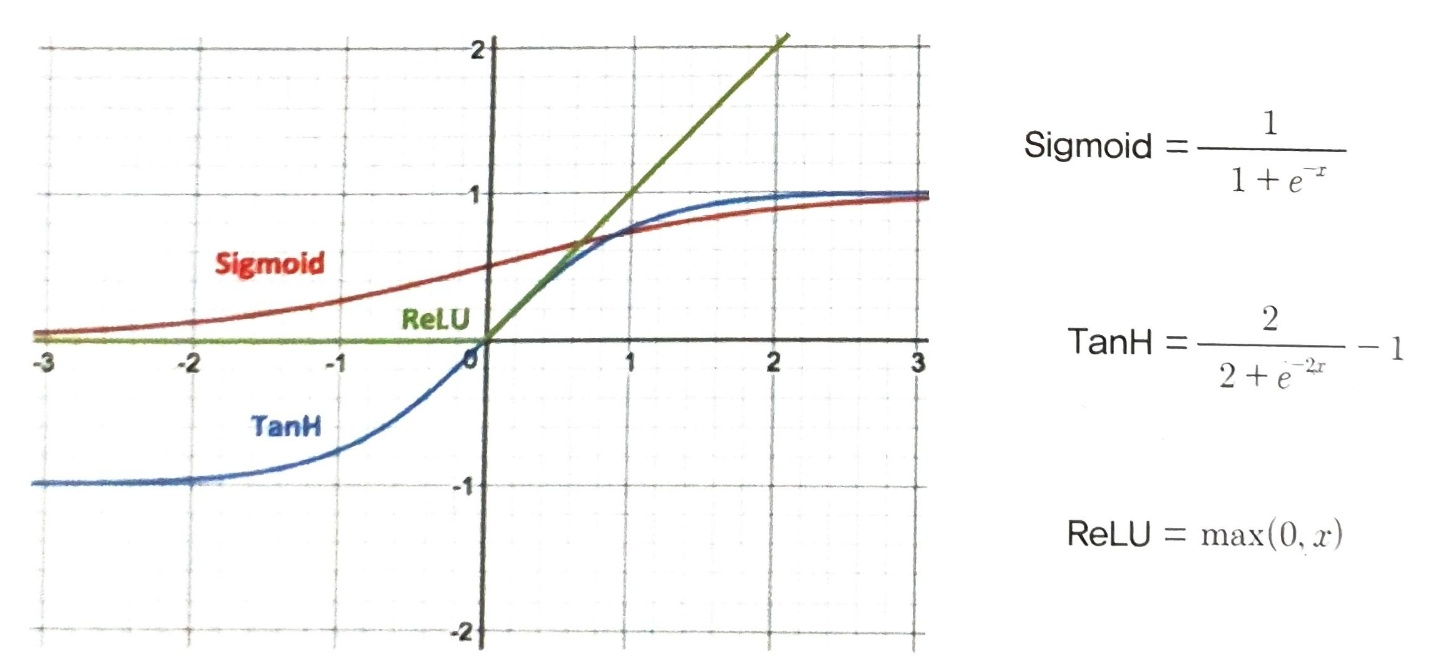
스텝 함수 대신 비선형 함수를 활성화 함수로 사용하는 이유는 역전파(Back propagation)를 사용한 모델 학습 시 활성화 함수가 미분 가능해야 하는데, 스텝함수는 미분이 불가능합니다.
신경망
다층 퍼셉트론은 퍼셉트론의 레이어가 여러 개 라는 뜻입니다. 하나의 퍼셉트론으로는 해결하기 어려웠던 문제를 해결하기 위해 여러개의 뉴런을 이용해 반든 것을 인공 신경망(Artificial neural network)라고 합니다.
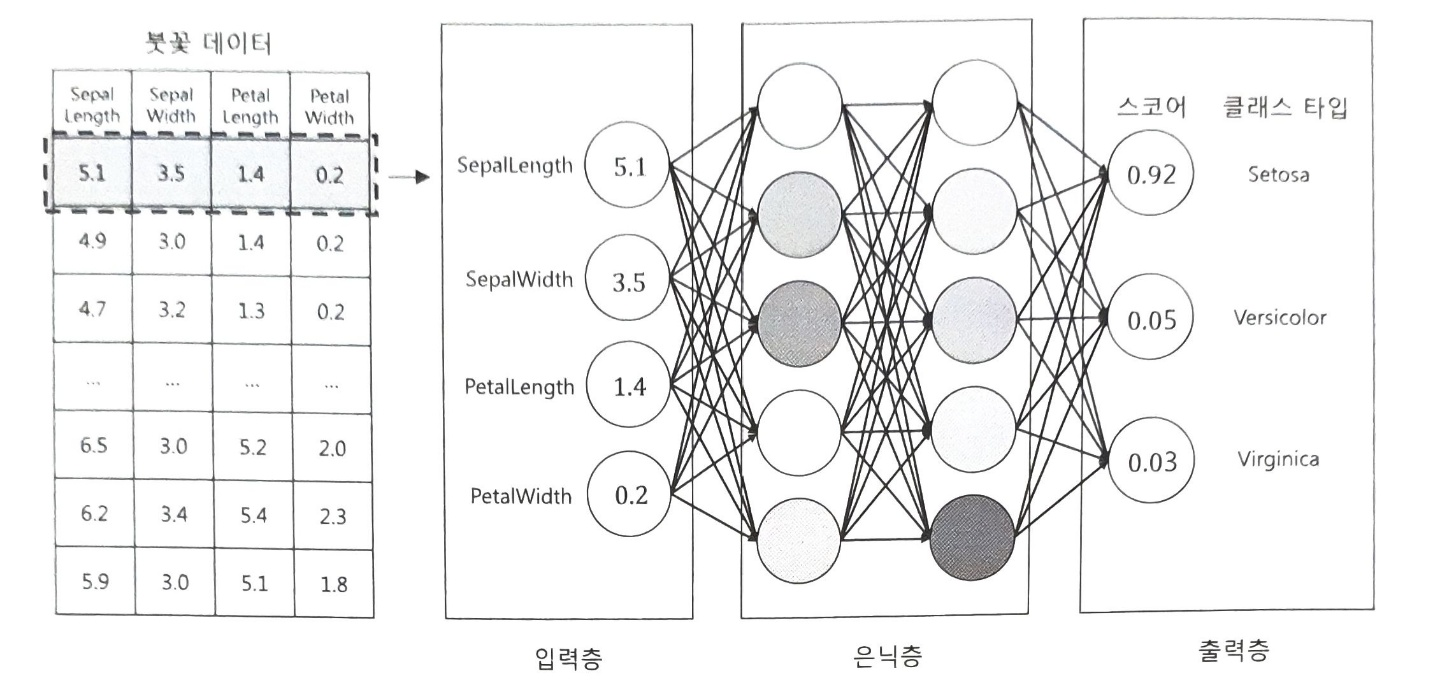
입력층(input layer)에 입력된 데이터는 출력층(output layer)에 도달하기전에 은닉층(hidden layer)라는 층을 거친 후 출력층에 도달합니다. 은닉층은 하나의 층 뿐만 아니라 여러개의 레이어로 구성될 수 있습니다.
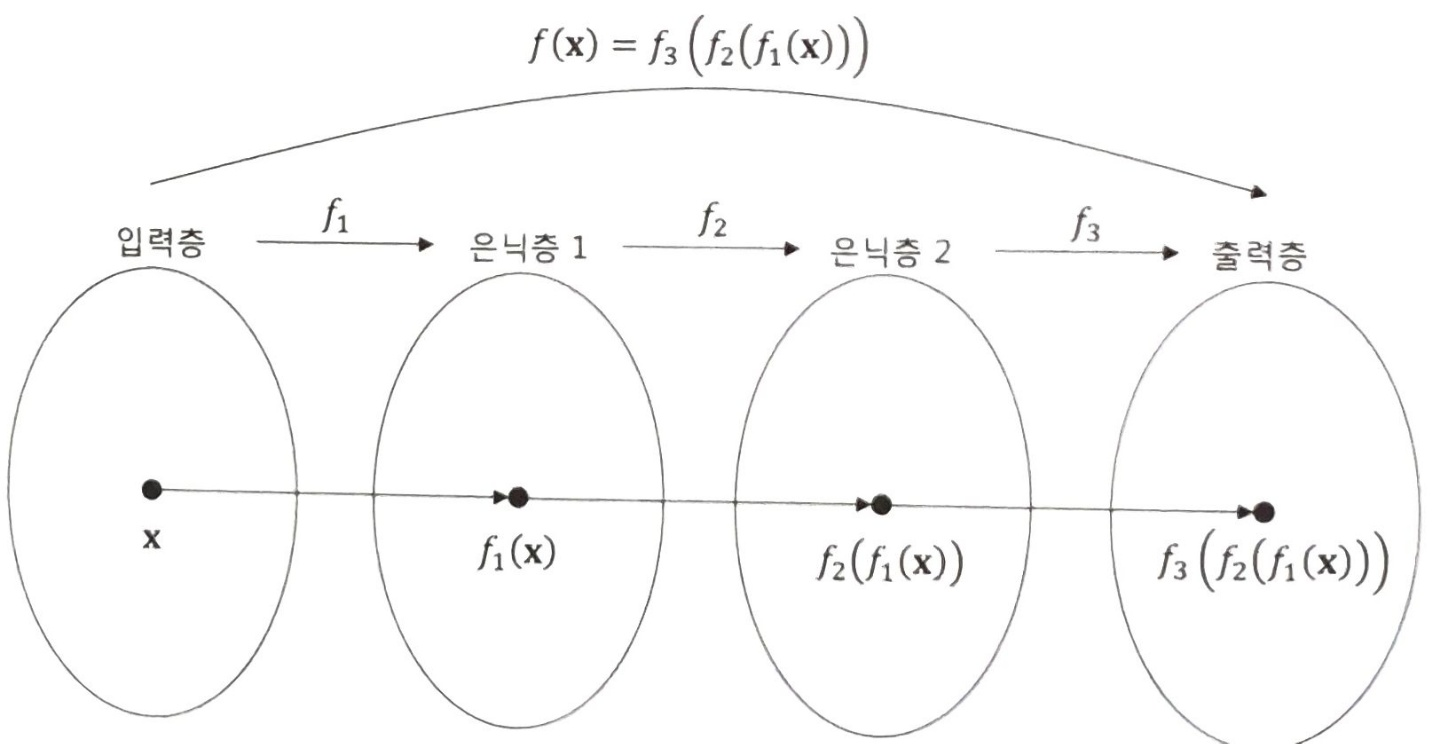
위와 같은 체인 구조(chain structure)는 신경망에서 자주 쓰이는 구조입니다.
신경망의 층이 깊을수록 함수의 개수는 많아지고, 합성 함수도 복잡해집니다. 합성 함수의 개수는 모형의 깊이(depth)를 의미합니다.
딥러닝 학습
다층 퍼셉트론에서 최적값을 찾아가는 과정은 역전파(Back propagation)방법을 사용합니다.
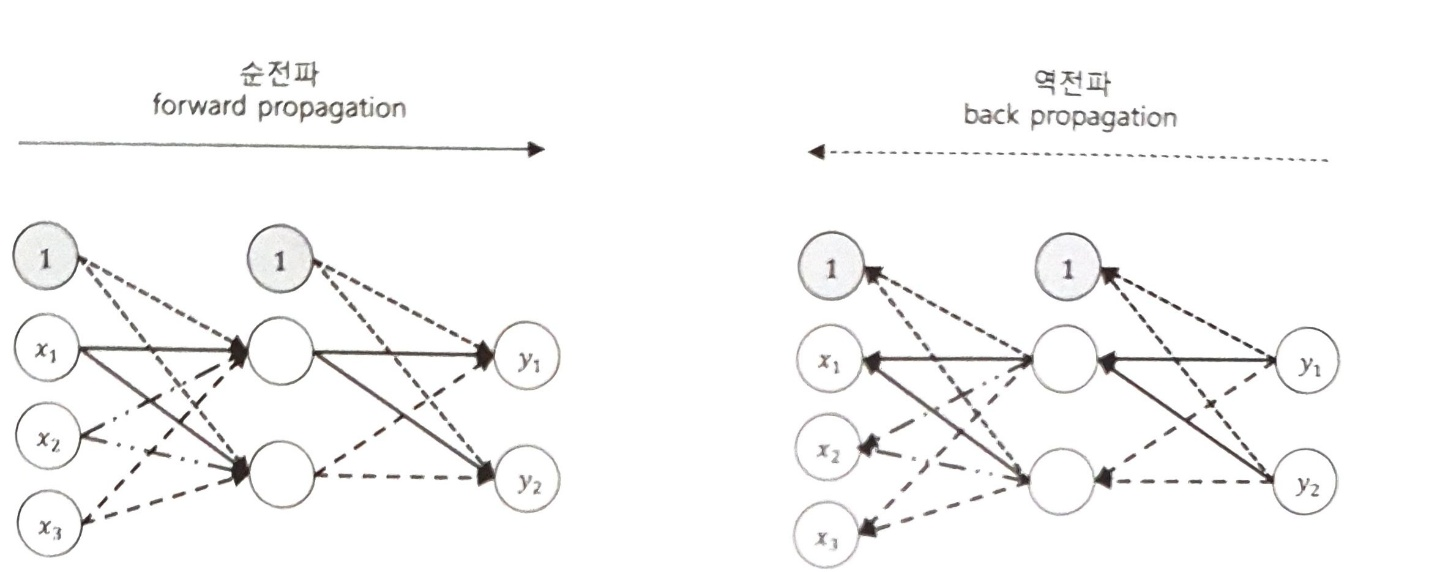
순전파 과정을 거치면 출력값 (y_hat)을 얻게되고, 정답과 출력값의 차이를 구합니다.
그 차이를 구하기 위해서 손실함수를 사용합니다. 옵티마이저는 손실함수를 최저로 하기 위해 역전파를 사용해 딥러닝 모델의 모든 매개변수를 변경합니다.
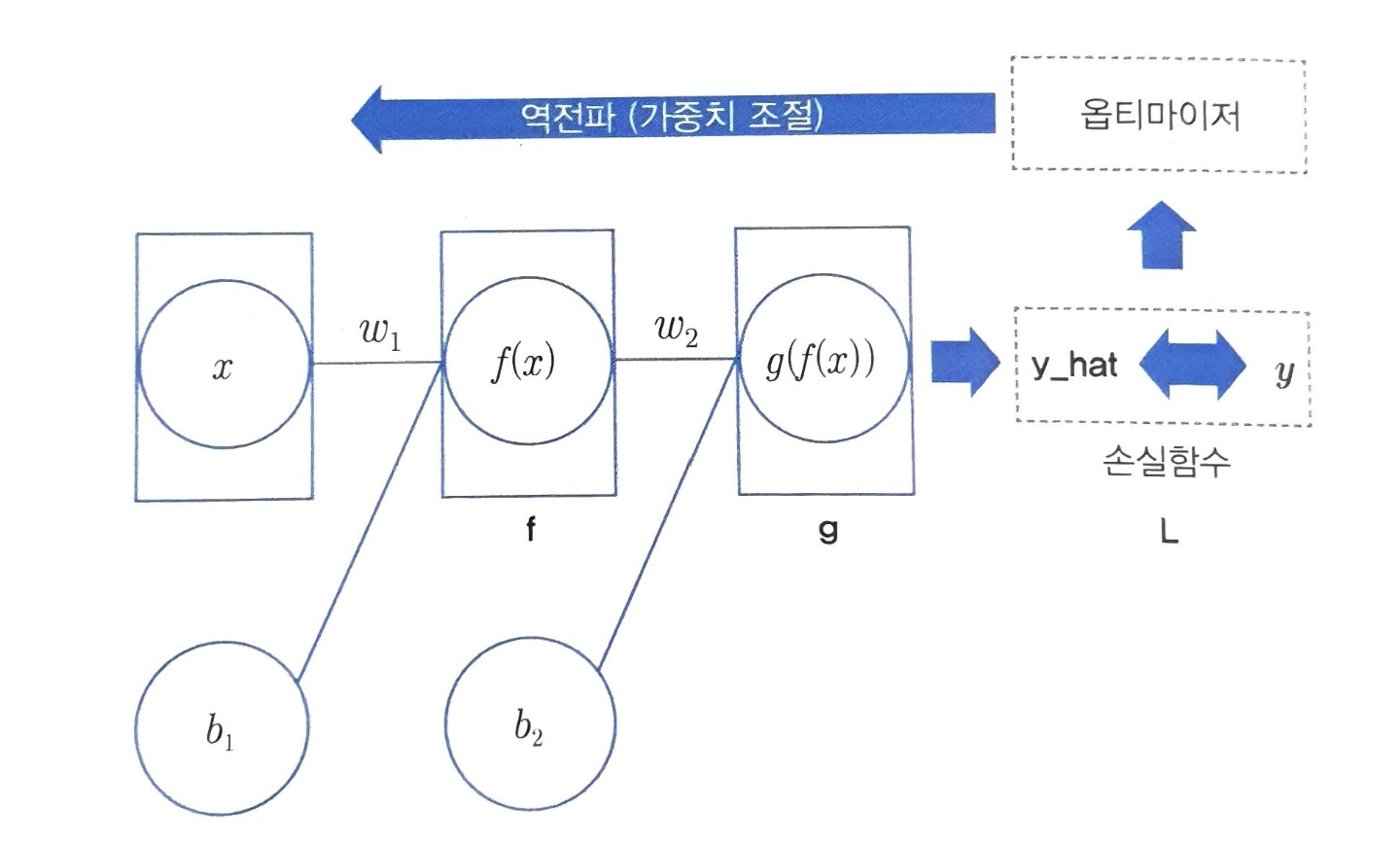
역전파 과정
- 가중치 초기화
- 순전파(foward propagation)를 통한 축력값 계산
- 비용 함수(cost function)정의 및 미분식 구하기
- 역전파(back propagation)를 통한 1차 미분값 구하기
- 파라미터(parameter) 업데이트
- 2~6과정 반복
