퍼셉트론 (Perceptron)

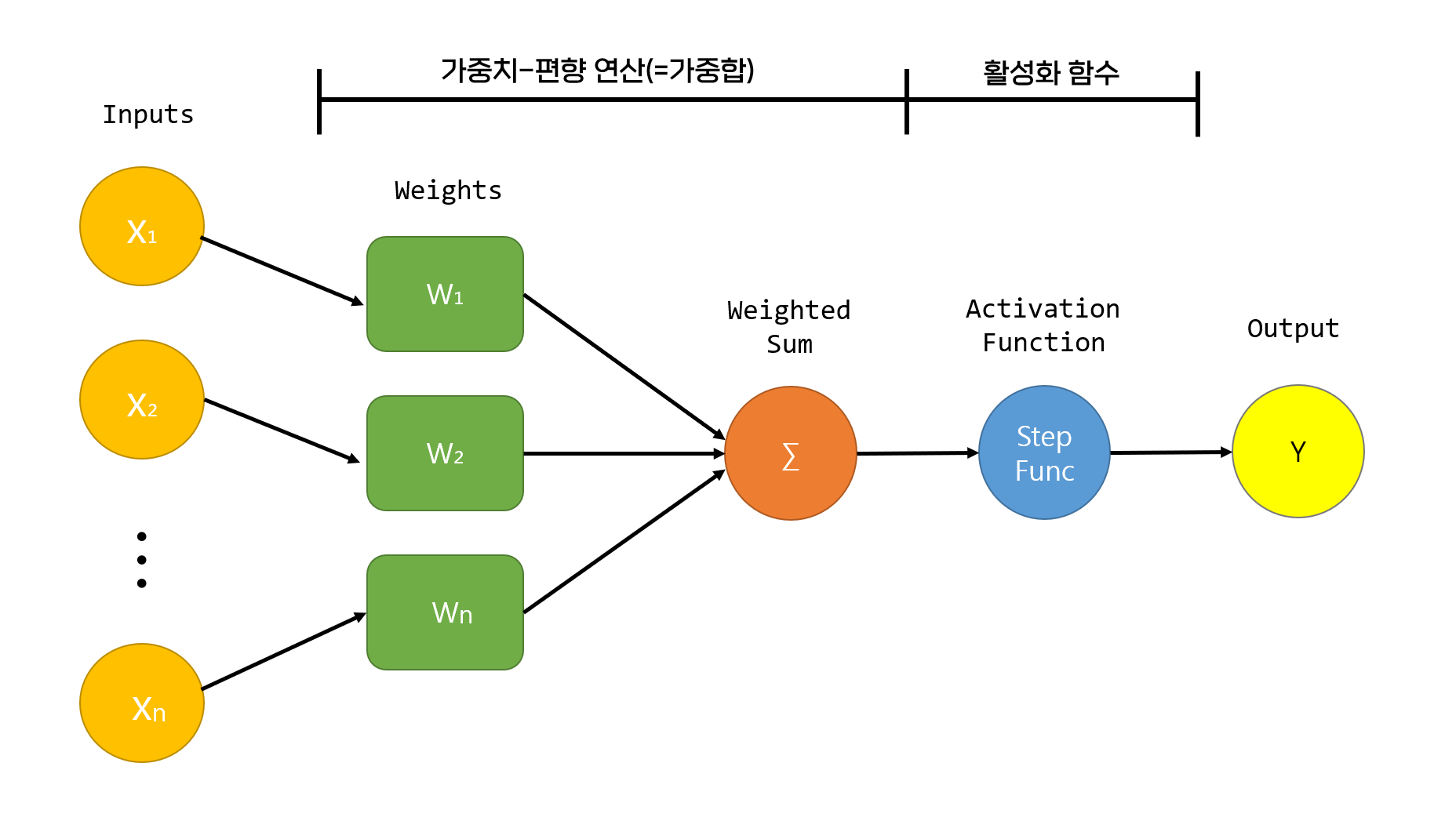
퍼셉트론은 다수의 입력을 받고 출력은 하나를 출력하는 구조의 신경망을 이루는 가장 기본 단위이다.

퍼셉트론은 단점을 가지고 있는데 바로 XOR 문제를 풀 수 없다는 점이다.

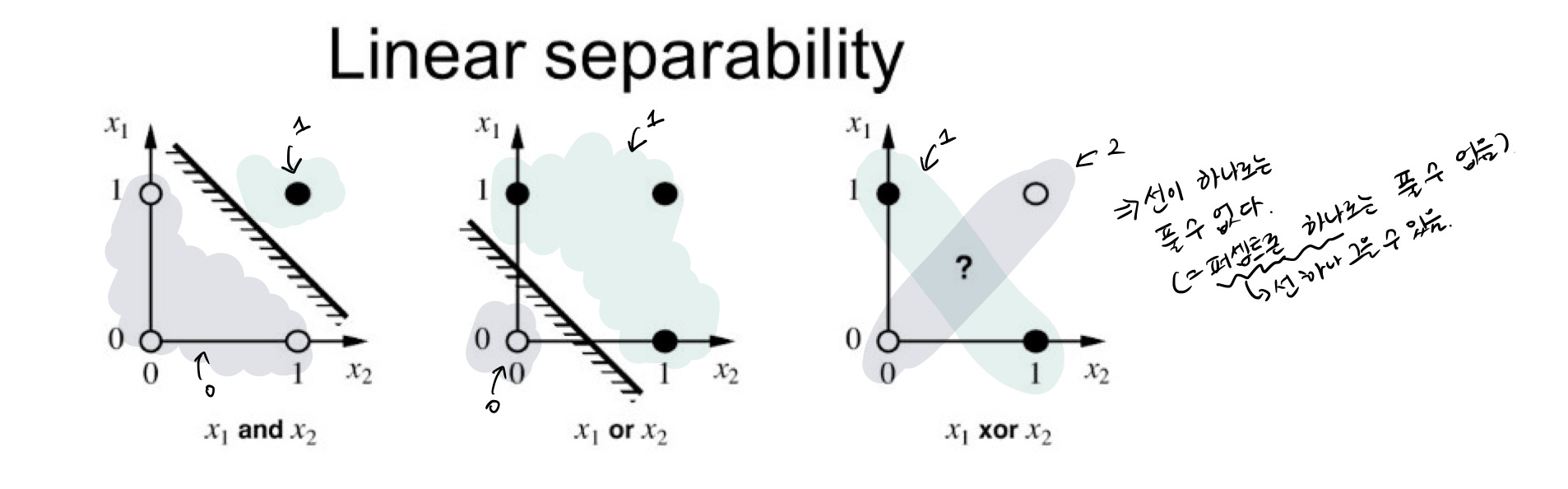
위의 그림에서 보이듯이 퍼셉트론은 AND 게이트나 OR 게이트에서는 사용할 수 있지만 XOR에서는 선 하나로는 풀 수 없다는 단점을 갖고 있다.

가중치(Weight)-편향(bias) 연산

퍼셉트론에 입력된 Input들을 각각의 가중치와 곱한 뒤 합해주는 연산이다.

input = np.array([1, 2, 3])
weight = np.array([0.3, -0.1, 0.1]) # 임의의 가중치들

np.dot(input, weight) # 0.4

위의 코드를 통해서 쉽게 가중합을 구할 수 있다.
np.dot을 하게 되면 내부에서는 다음과 같은 연산이 일어나게 된다.

1 * 0.3 + 2 * (-0.1) + 3 * 0.1 = 0.4

활성화 함수 (Activation Function)

Step Function

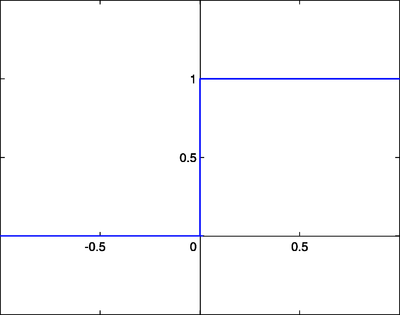
계단 함수는 위의 그림과 같이 임계값을 넘기면 1, 아니면 0을 출력하는 함수이다.

Sigmoid Function

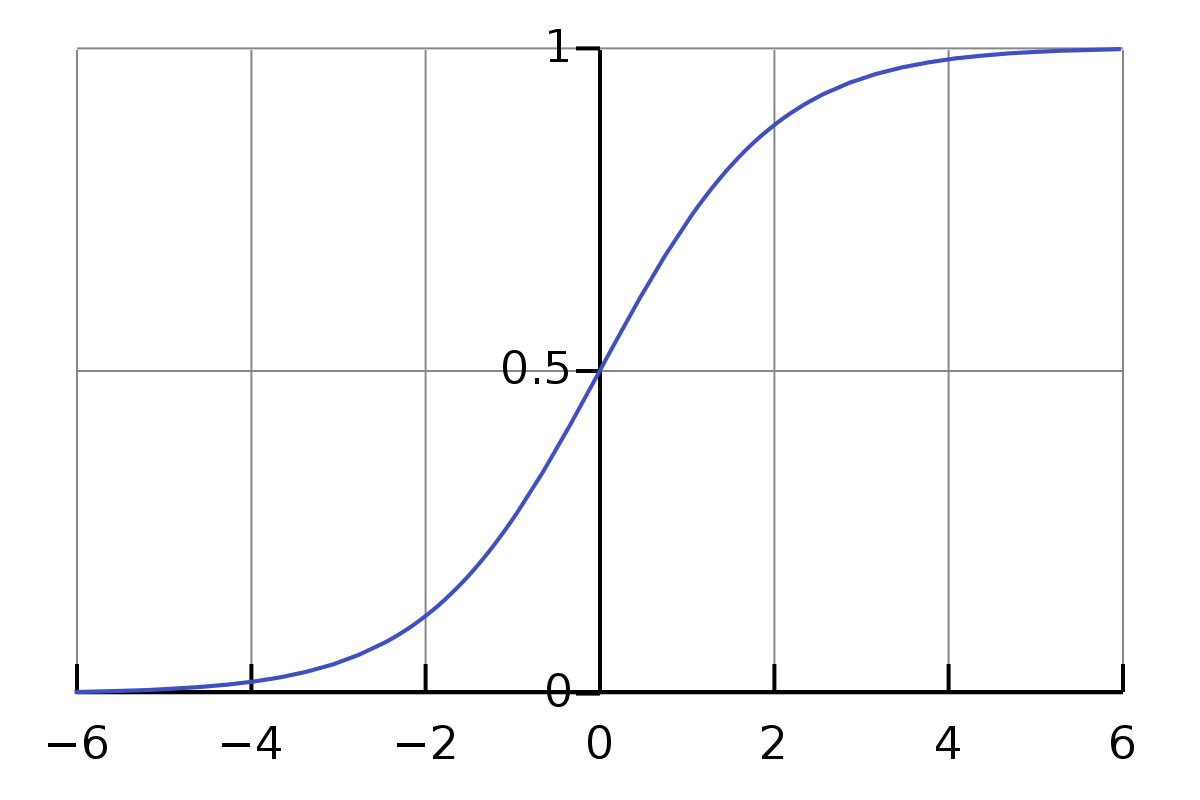
계단 함수는 임계값 지점에서 미분이 안되고, 나머지 지점에서는 미분값이 0이 나온다는 단점이 있는데 시그모이드 함수는 이러한 계단 함수의 단점을 해결하기 위해서 사용하는 함수이다.

시그모이드 함수는 모든 지점에서 미분이 가능하며 임계값보다 작은 값은 0에 가까워지고 큰 부분은 1에 가까워지게 된다.

ReLU Function

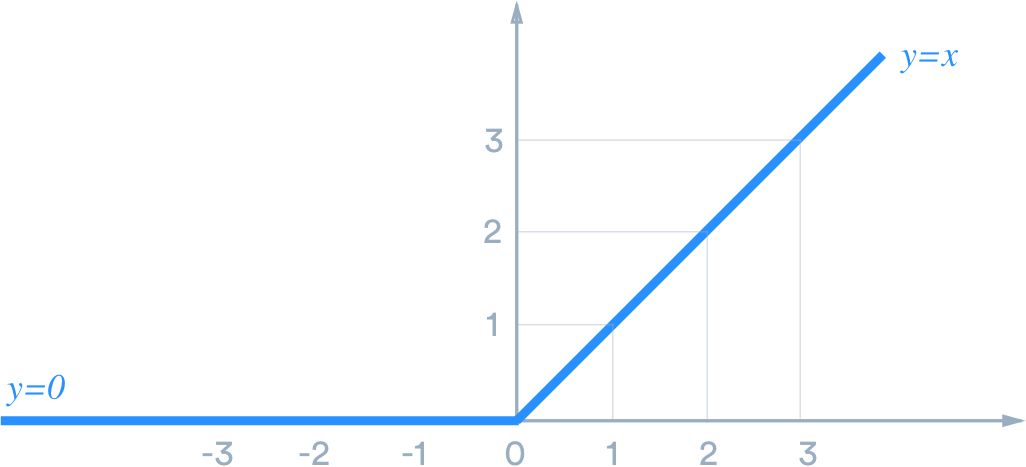
시그모이드 함수는 중복해서 사용할 때 기울기 소실(Vanishing Gradient)가 발생하게 되는데 이러한 문제점을 해결하기 위해서 등장한 함수가 ReLU 함수이다.

ReLU 함수는 양의 값이 입력되면 그 값을 그대로 출력하고 음의 값이 입력되면 0을 출력해준다. 음의 값은 0을 반환하기 때문에 몇몇 가중치들이 업데이트 되지 않는다는 단점을 갖고 있다.

Sotfmax Function

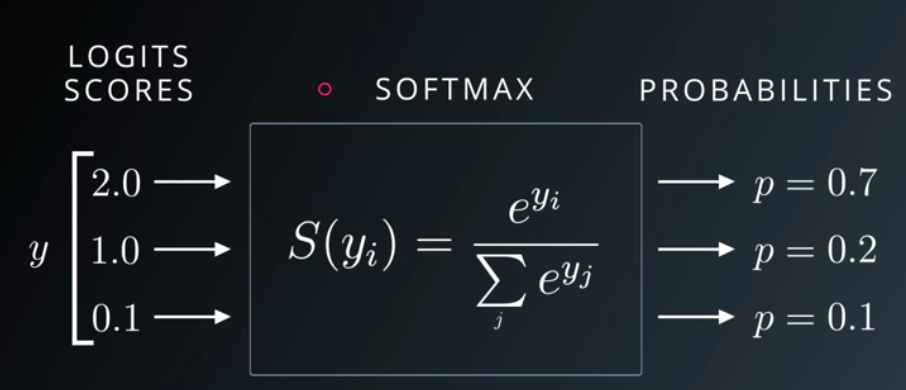
소프트맥스 함수는 다중 분류 문제에 적용할 수 있도록 시그모이드 함수를 일반화한 함수이다. 가중합 값을 통과시키면 모든 클래스의 값의 합이 1이 되는 확률값으로 변환시켜준다.