재귀와 분할 정복법

재귀란 무엇인가?

작업 중에 자기 자신을 호출 하는 것을 재귀 호출(recursive call)이라 하고, 재귀 호출을 하는 함수를 재귀 함수(recursive function)라 부릅니다.

베이스 케이스(base case)

• 재귀 함수 안에서 재귀 함수를 부르지 않고 return 하는 경우를 뜻합니다.

재귀 함수 템플릿

(반환값형) func(인수) {
	if (베이스 케이스) {
		return 베이스 케이스에 대응하는 값;
	}

	// 재귀 호출
	func(다음 인수);
	return 응답;
}

재귀 사용의 예시들

유클리드 호제법

재귀 함수를 사용해서 명쾌하게 서술 가능한 알고리즘의 대표적인 예시로, 최대 공약수($GCD(m,n)$)를 구하는 알고리즘입니다.

int GCD(int m, int n) {
  // 베이스 케이스
	if (n == 0) return m;

  // 재귀 호출
	return GCD(n, m % n);
}

• 유클리드 호제법의 복잡도는 $m ≥ n > 0$ 이면 $O(log n)$입니다.

피보나치 수열

int fibo(int N) {
	// 베이스 케이스
	if (N == 0) return 0;
	else if (N == 1) return 1;

	// 재귀 호출
	return fibo(N - 1) + fibo(N - 2);
}

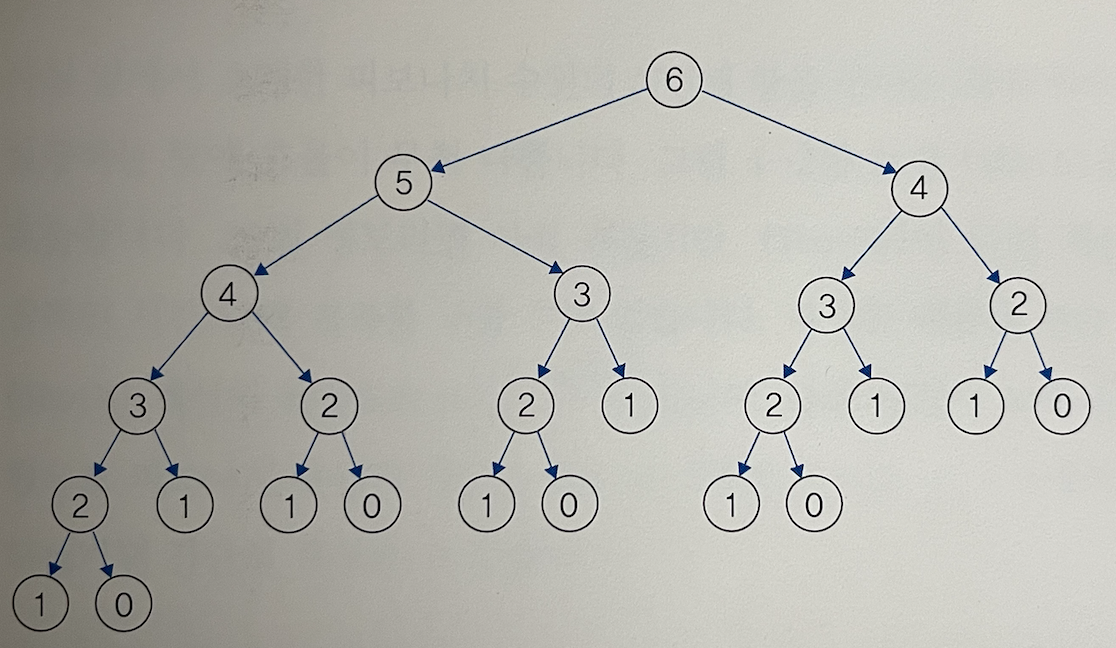
• 같은 계산을 몇 번이나 계속 실행하므로 효율이 무척이나 나쁩니다.
  • 예를 들어, fibo(4)를 위 사진에서 왼쪽에서 계산했는데, 오른쪽에서 또 fibo(4)를 계산해야 합니다.
  • 마찬가지로 fibo(3), fibo(2) 또한 모두 똑같겠죠?
• 계산 시간이 N에 대한 지수 시간이 나오게 됩니다.

재귀 함수를 사용한 전체 탐색

부분합 문제

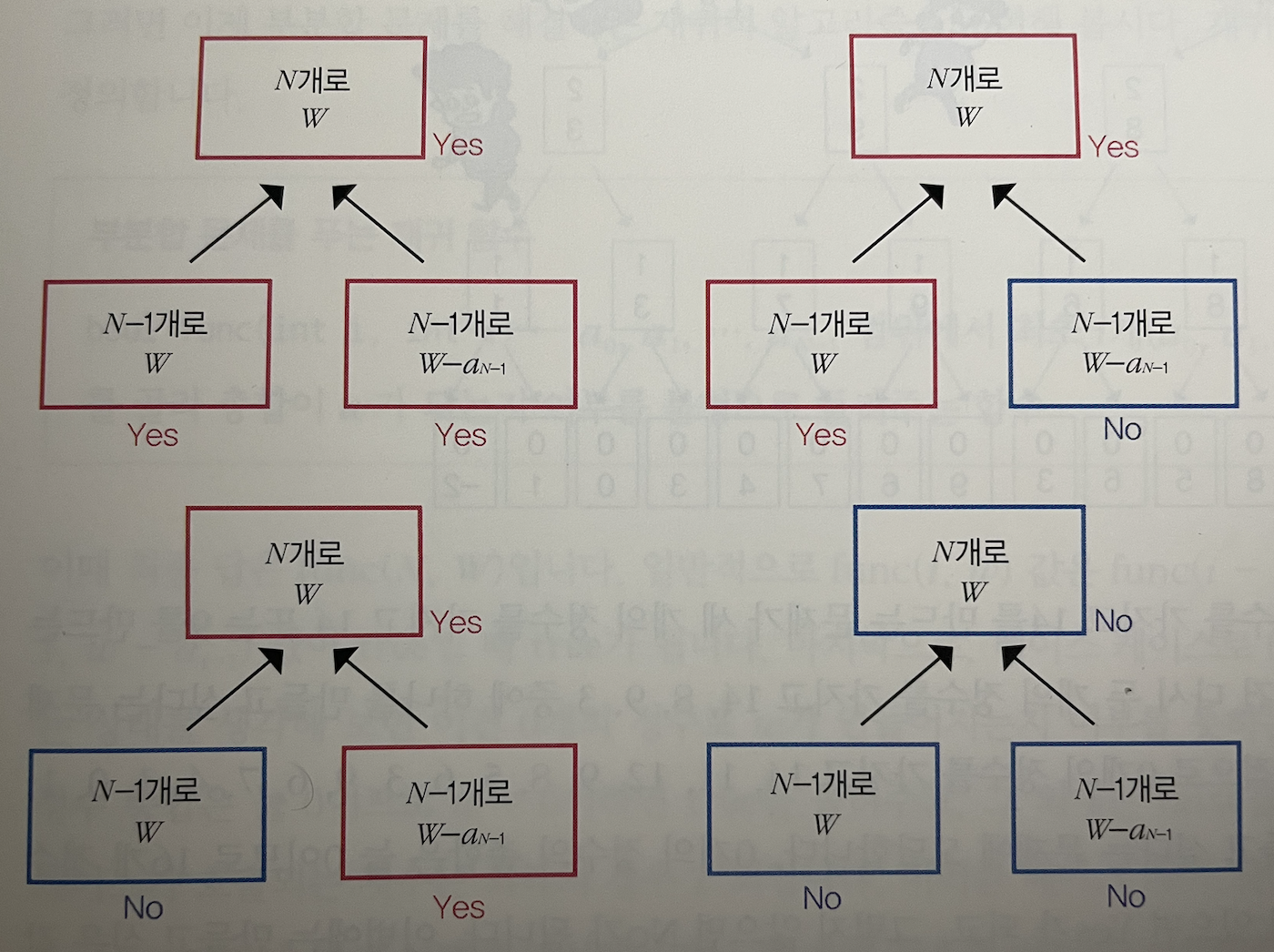
• 처음에는 N개의 정수에 관한 문제에서, 재귀적으로 생각하면 그 다음에는 N-1개의 정수에 관한 문제로 바뀝니다.
• 기본적인 재귀함수를 통한 해결은 최악의 경우 모두 No인 경우 $2^N$가지 선택지를 모두 조사해야 한다는 것입니다. 그렇다면 복잡도는 $O(2^N)$이므로 굉장히 비효율적입니다.

메모이제이션 동적 계획법

위에서의 피보나치 수열이나 부분합 문제에서 처럼 계속 중복해서 계산하는 것이 아닌, 이전에 계산한 값을 메모리에 저장해두고 같은 인수라면 저장해 둔 값을 돌려줍니다.

캐시(cache) 방식

• 메모이제이션을 사용하면 복잡도는 $O(N)$이 됩니다.

vector<long long> memo;

long long memoFibo(int N) {
  // 베이스 케이스
	if (N == 0) return 0;
	else if (N == 1) return 1;

  // 메모 확인(이미 계산한 값이면 반환)
	if (memo[N] != -1) return memo[N];

  // 답을 메모하면서 재귀 호출
	return memo[N] = memoFibo(N - 1) + memoFibo(N - 2);
}

분할 정복법

주어진 문제를 몇 가지 부분 문제로 분해한 후 각 부분 문제를 재귀적으로 풀고 그 답을 조합해 원래 문제의 답을 구성합니다.

• 이미 다항식 시간이 걸리는 알고리즘을 구한 문제에 대해 좀 더 빠른 알고리즘을 설계하기 위해 의식적으로 분할 정복법을 사용합니다.

동적 계획법

주어진 문제 전체를 일련의 부분 문제로 잘 분해해 각 부분 문제의 답을 메모이제이션하면서 작은 부분 문제에서 큰 부분 문제로 순서대로 답을 구하는 방법입니다.

동적 계획법 관련 개념도

완화

• 일단 배열 dp 에서 각 값이 점점 작아지는 값으로 갱신되어 가는 분위기만 파악해봅시다.
• 아주 큰 값으로 초기화되어 있는 배열을 minimum 값으로 교체하는 작업입니다.
  • 상황에 따라서는 maximum 값이 될 것입니다.

template<classT>
void chmin(T &a, T b) {
	if (a > b) a = b;
}

끌기 전이 형식과 밀기 전이 형식

• 끌기 전이 형식은 이전 값을 사용하여 현재 값을 갱신하는 방법입니다.
• 밀기 전이 형식은 현재 값을 사용하여 이후의 값을 갱신하는 방법입니다.

❗️그래프에서, 꼭지점 u에서 꼭지점 v로 전이하는 변에 관한 완화 처리가 성립하려면, dp[u] 값이 확정이어야 합니다.

전체 탐색 메모이제이션을 이용한 동적 계획법

재귀함수가 한 번 호출되어 같은 인수의 해답을 알고 있다면, 그 시점에 해답을 메모이제이션 해야합니다.

knapsack problem

우선 시험 삼아 동적 계획법의 부분 문제를 다음과 같이 정의해보겠습니다.

dp[$i$] ← 최초 $i$개의 물건 {${ 0, 1, …, i - 1 }$} 중에서 무게가 W를 넘지 않도록 고른 가격 총합의 최대값

그런데 위 내용뿐이라면, 부분 문제 사이의 전이를 만들 수 없어 풀이가 막히게 됩니다.

그래서 아래와 같이 한 번 더 변경해보겠습니다.

dp[$i$][$w$] ← 최초 $i$개의 물건 {${ 0, 1, …, i - 1 }$} 중에서 무게가 $w$를 넘지않도록 고른 가격 총합의 최대값

위와 같이, 일단 만들어 본 테이블 설계로 전이가 제대로 되지 않을 것 같으면 점점 인덱스를 추가해서 전이가 성립하도록 하는 작업을 반복합니다.

편집 거리

두 문자열 S, T가 얼마나 닮았는지 그 유사성을 측정하는 방법입니다.
dp[$i$][$j$] ← S의 $i$번째까지의 문자열과 T의 $j$번째까지의 문자열 사이의 편집 거리

구간 분할 최적화

일렬로 나열한 N개의 대상물을 구간으로 나누어 분할하는 방법을 최적화 해봅시다.

dp[$i$] ← 구간 [0, $i$)에 대해 구간을 분할하는 최소 비용