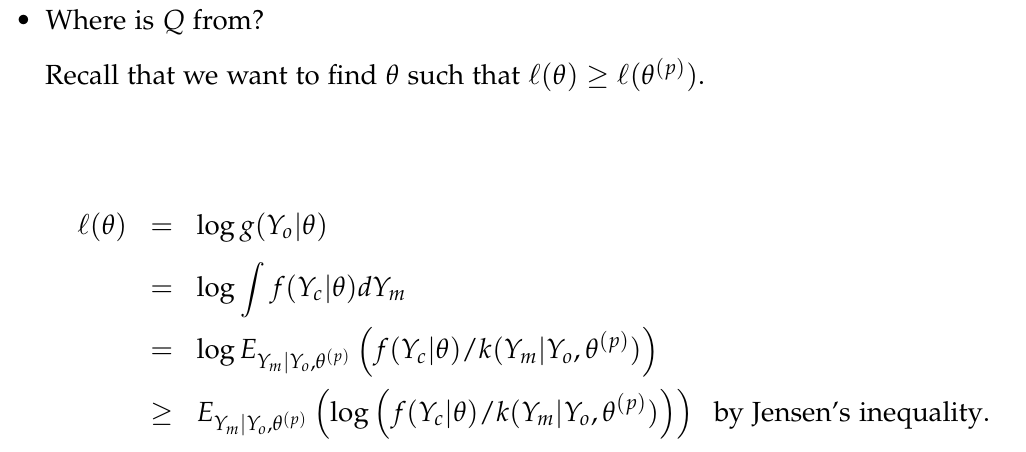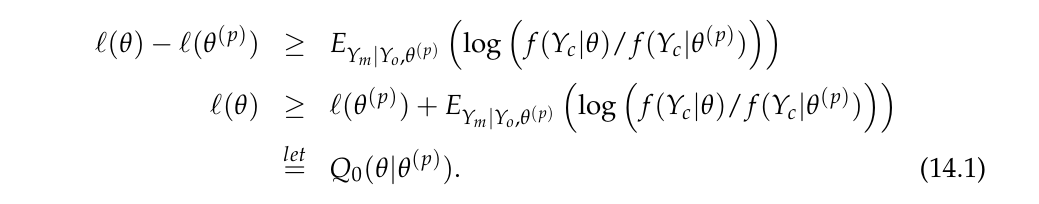EM algorithm

Definition

EM은 Expectation-Maximization 의 준말이다

Motivation

Example

우리가 알고 있는 단순선형 회귀모델을 생각하자.

$Y_i = X_i\beta + \epsilon_i$ , $i = 1,2,....n$

우리가 일반적으로 가정하는 상황은, $X_1,....X_n$ 그리고 $y_1.... y_n$ 을 알고있는 상황이다.

이 경우에서, $(X_i, y_i), i = 1,2,3...n$ 은 Complete data라고 할 수 있다

만약, 우리가 $y_1 .... y_n$ 을 여전히 알고 있지만,
$X_1 ... X_m$ 까지만 알고 $X_{m+1}.... X_n$ $(m < n)$을 모르는 상황에 있을 때, 어떻게 회귀계수 $\beta$ 를 추정하는 것이 좋을까?

이 때는, $(X_1,... X_m, y_1 ... y_n)$ 은 observed data라고 생각 할 수 있고, $X_{m+1} ... X_n$ 은 missing data라고 생각 할 수 있다.

물론, $i = m+1 ... n$ 까지의 데이터를 날리고 추정하는 것도 하나의 방법이지만, EM 알고리즘은 이런 경우에 활용 가능한 최적화 알고리즘을 제공한다.

이와 같은 단순한 문제 뿐만 아니라, missing data problem으로 변환할 수 있는 대부분의 추정문제(보통 latent variable을 도입하는 형태로 많이 이루어진다)에서, EM 알고리즘은 활용될 수 있다.

Algorithm

알고리즘을 설명하기에 앞서, 다음과 같은 용어를 정의한다

• $Y_c$ : Complete Data
• $Y_o$ : Observed Data

EM 알고리즘은 다음의 단계로 구성된다.

E-Step

$Q(\theta | \theta_0) = E_\theta logf(Y_c |Y_o , \theta_0)$ 을 구한다.

What is $Q$ ?

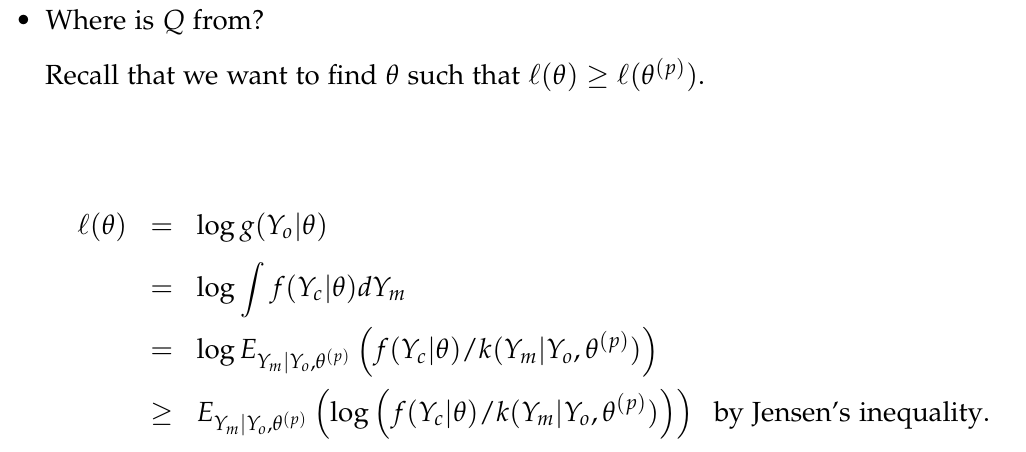
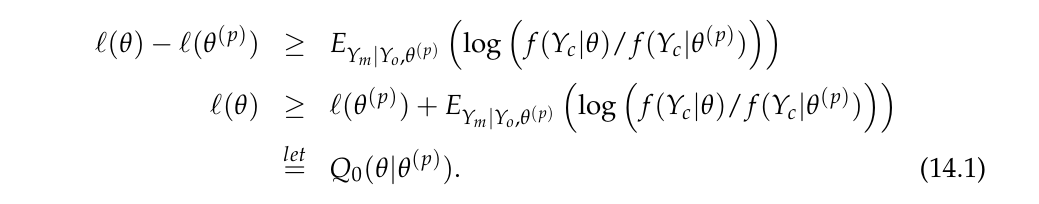
즉, $l(\theta)$의 lower bound를 최대화시키는 작업을 반복하면, $argmax_{\theta}\;l(\theta)$의 근사치를 찾을 수 있을 것이라는 발상이다.

M-Step

E-step에서 구한 $Q$를 maximize 시키는 새로운 $\theta$ 를 구하고, 이를 새로운 $\theta_0$로 업데이트 시킨다.

Iteration
$\theta$ 가 만족스러운 값에 수렴 할때까지 이를 반복한다.

비교적 간단하지 싶으면서도, 왜 이런 알고리즘이 만들어졌는지에 대한 부연설명을 간단히 해보겠다.(본인의 주관적인 의견도 포함되었으니 비판적으로 수용바람)

일단은, 우리가 좋은 모수를 추정하기 위해 하려고 하는 것은, Observed Data $Y_o$ 하에서 Likelihood를 최대화시키는 $\theta$를 찾는 것이다. ($argmax_{\theta}\;logf(Y_o | \theta)$)

Complete Data $Y_c$의 경우엔, 우리가 비교적 쉽게 log-likelihood를 구할 수 있는 상황이 많다. (motivation part에서의 예시만 봐도 그러하다) 또한, 구하기 쉽지 않다면, latent variable를 도입하여 표현이 용이하게끔 할 수 있다.

그러나, Observed Data $Y_o$의 경우 $logf(Y_o | \theta)$ 를 구하기 힘든 상황이 많다. 당장 motivation의 상황만 보더라도, 저 상황에서의 log-likelihood를 어떻게 표현 할 것인가?

따라서, 비교적 구하기 쉬운 complete data에 관한 log-likelihood를 이용하여 $logf(Y_o | \theta)$ 를 최적화시키는 알고리즘을 고안한 것이 EM알고리즘이라고 생각하면 될 것이다. 이 알고리즘이 어떻게 이를 가능케 하는지는 이어서 설명하도록 하겠다.

Why it works

EM Algorithm은 두 가지 유용한 성질이 있다.

1. EM 알고리즘에 의해 Update 되는 $\theta$는 $logf(\theta | Y_o)$ 를 단조증가 시킨다. (monotonicity)

2. $logf(\theta | Y_o)$ 는 $l$이 bounded from above라는 조건 하에서 특정값 $l^*$로 수렴한다. 이 때, $l$이 unimodal이면 $l^*$가 global maximum 이 되지만, 일반적으로는 local maximum이다.

(참고 : unimodality)
https://en.wikipedia.org/wiki/Unimodality

본 포스트에서는 1번의 증명만을 다루도록 하겠다.

$Q(\theta|\theta^{(p}) = \int logf(Y_c|\theta)k(Y_m|Y_o, \theta^{(p)})dY_m$
$=E_{Y_m|Y_o,\theta^{(p)}}(logf(Y_c|\theta))$
$=l(\theta) + H(\theta|\theta^{(p)})$
$where \; H(\theta|\theta^{(p)}) = \int logk(Y_m|Y_o,\theta)k(Y_m|Y_o,\theta^{(p)})dY_m$


$Q(\theta^{(p+1)}|\theta^{(p)}) = l(\theta^{(p+1)}) + H(\theta^{(p+1)}|\theta^{(p)})$
$Q(\theta^{(p)}|\theta^{(p)}) = l(\theta^{(p)}) + H(\theta^{(p)}|\theta^{(p)})$
$Q(\theta^{(p+1)} \mid \theta^{(p)}) - Q(\theta^{(p)} \mid \theta^{(p)}) = \left\{\ell(\theta^{(p+1)}) - \ell(\theta^{(p)})\right\} + \left\{H(\theta^{(p+1)} \mid \theta^{(p)}) - H(\theta^{(p)})\right\}$
$Q(\theta^{(p+1)} \mid \theta^{(p)}) \geq Q(\theta^{(p)} \mid \theta^{(p)})$ by the definition of EM
$H(\theta^{(p+1)} \mid \theta^{(p)}) \leq H(\theta^{(p)} \mid \theta^{(p)})$ by the following using Jensen’s inequality


$\begin{aligned} &\int \log \, k(Y_m \mid Y_0, \theta^{(p+1)}) k(Y_m \mid Y_0, \theta^{(p)}) dY_m - \int \log \, k(Y_m \mid Y_0, \theta^{(p)}) k(Y_m \mid Y_0, \theta^{(p)}) dY_m \\ &\quad = \int \log \left( \frac{k(Y_m \mid Y_0, \theta^{(p+1)})}{k(Y_m \mid Y_0, \theta^{(p)})} \right) \times k(Y_m \mid Y_0, \theta^{(p)}) dY_m \leq \log \int k(Y_m \mid Y_0, \theta^{(p+1)}) dY_m = 0 \end{aligned}$
$\text{Therefore } \ell(\theta^{(p+1)}) \geq \ell(\theta^{(p)}).$

Application

(작성중)

Reference

• 서울대학교 통계학과 응용통계1 강의록
• https://velog.io/@claude_ssim/기계학습-Expectation-Maximization-EM