푸리에 변환과 주파수 해상도

푸리에 변환은 신호를 무한한 시간 동안을 대상으로 하기 때문에 유한한 시간의 샘플을 사용하면서 샘플의 끝 구간의 문제로 인해 오류 정보를 가지게 된다. 어치파 현실적으로 활용하려면 샘플의 수는 제한될 수 밖에 없으니 오류를 해결할 방법을 만들어야 한다.

이를 해결하기 위해서 사용하는 방법이 윈도우 함수이다. 즉 fft를 사용하기 위한 제한 조건이 n = 2^m으로 제한된다는 것인데, 이 때 n은 fft size라고 하며 신호의 주파수를 얼마나 세밀하게 분석할 수 있는지 따지는 주파수 해상도에 영향을 준다.

윈도우

윈도우는 샘플된 구간의 맨 앞쪽과 뒤쪽의 신호가 0으로 변하게 한다. 그리고 나머지 구간을 모두 0으로 간주하도록 유도한다. 그러면 푸리에 변환의 무한대 시간 영역 조건을 샘플된 신호 구간으로 좁힐 수 있다.

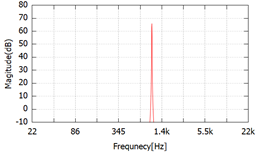
1000HZ의 신호를 윈도우를 사용하지 않고 푸리에 변환을 하면 예상과 다르게 다른 주파수 성분이 같아보이게 된다. 이를 로빙 오류라고 한다. 좌우에 로빙 오류가 펼쳐 있어 모양을 사이드 로브라고 한다. 이 사이드 로브에 의해 푸리에 변환의 결과에서 정확한 결과가 얻기 어려워 진다.

• 전

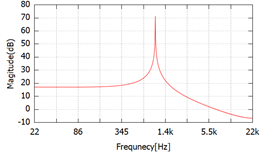
• 후

출처: https://medialink.tistory.com/135