Machine Learning with PyTorch and Scikit-Learn_chapter2

Chapter2: Perceptron & Adaptive linear neuron(Adaline)

2.1. Perceptron & Adaline

• Perceptron과 Adaline은 머신러닝의 기초 개념.

• Adaline은 Classification을 위한 더 발전된 알고리즘인 regression, logistic regression, Supprot Vec/tor Machine의 토대를 마련.

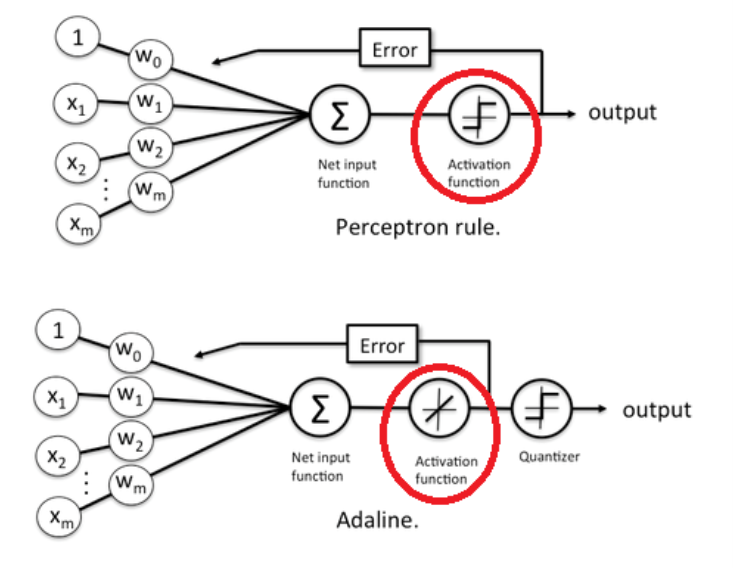
• Perceptron과 Adaline의 차이: 가중치 업데이트를 위한 Activation Function이 다름.
  

• Perceptron의 Activation function은 Net input function의 return값을 임계값과 비교하여 결과에 따라 -1 또는 1을 return.
  -> 가중치 업데이트는 이 return값(-1 또는 1)과 실제 결과값(y; -1 또는 1)이 동일한지 그렇지 않은지에 따라 진행됨.

• Adaline의 Activation function은 단순히 -1 또는 1에 대한 비교가 아니라, Net input function의 return값과 실제 결과값(y)의 오차(Error)가 최소화되도록 가중치 업데이트(다시 말해, 임계값과의 비교를 통해 가중치를 업데이트 하는 것이 아님).
  -> Adaline 모델에서 Activation function을 거쳐, (예측값 – 실제값)을 구하기 위해, Loss function을 사용하는데, Loss function은 MSE(Mean Squared Error)를 통해 계산.
  -> Loss function은 모델을 통해 계산된 예측값과 실제값의 오차를 계산하는 함수로, Deep Learning 모델은 이 오차를 최소화하는 방향으로 진행(오차를 최소화 하는 parameter들을 찾는 것이 학습의 목적, 이때 사용되는 알고리즘을 Optimizer라 함).
  -> 이 때, Gradient 방식이 사용. 실제값과 예측값의 차이가 있으면, Gradient descent로 가중치 업데이트(Gradient descent는 신경망 모델에서 오차를 최소화하도록 하는 방법이자, 가장 기본적인 optimizer)

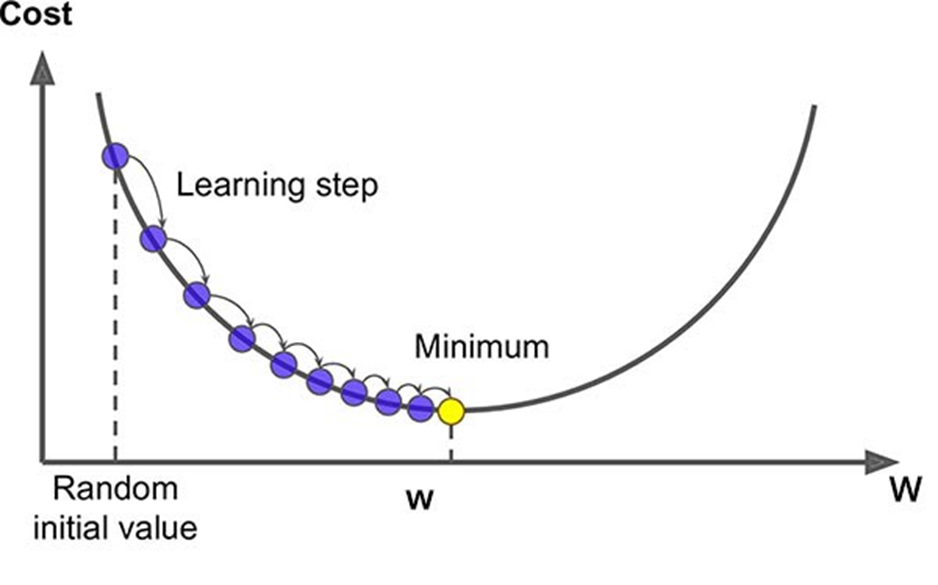
2.2. Gradient descent

• Gradient descent는 learning rate(𝜂)가 적절해야 함(값이 너무 크면 발산, 값이 너무 작으면 작업 속도가 느려지고, local minimum에 빠질 우려가 있음).
  -> 𝜂(에타)는Hypter parameter 이기 때문에 그 값을 결정할 때, k-fold validation 방법을 적용.

• Feature scaling을 통해 Gradient descent 결과를 좋게 할 수 있음. 대표적인 Feature scaling으로는 Standardization(표준화)가 있음.
  -> Feature Scaling은 Feature들의 크기와 범위를 정규화시키는 것.
  -> Standardization(표준화): 각 특성의 평균을 0에 맞추고, 특성의 표준 편차를 1로 만듬.

2.2.1. (full) batch gradient descent: batch_size = size of training data set

2.2.2. stochastic gradient descent(SGD) : batch_size = 1

• SGD장점: Shooting이 발생하여 local minimum에 빠질 위험성이 적고 수렴 속도가 상대적으로 빠름.
• SGD단점: global minimum을 찾지 못할 가능성이 큼.

2.2.3. mini-batch gradient descent : 1 < batch size < size of training data set

• Compromise between full batch gradient descent and SGD

2.3. 용어

Epoch: One Epoch is when an ENTIRE dataset is passed forward and backward through the neural network only ONCE.

• 1 epoch은 data set 전체에 대해 1번 학습을 완료한 상태.
• epoch은 underfitting 또는 overfitting에 영향을 미침.
  -> epoch의 횟수가 너무 많으면 overfitting에 대한 위험이 있고, 반대로 너무 적으면 underfitting에 대한 위험이 있다.

Batch size: Total number of training examples present in a single batch.

• 한 번에 학습시키는 data의 수.
  -> batch_size 100 => 한 번에 100개의 data를 학습시킨다.

Iteration: The number of passes to complete one epoch.

• 1epoch data/batch_size
  -> data가 1,000개 batch size가 10이면 '100 iteration'

예) 100,000개의 data set을 학습한다고 가정했을 때,
batch_size = 10,000 iteration = 10 epoch = 10

Loss function(손실함수)와 Cost function(비용함수)

• 크게 보면, 두 개념의 차이는 없음.

Loss function is usually a function defined on a data point, prediction and label, and measures the penalty. -> single data set에 대한 것.

Cost function is usually more general. It might be a sum of loss functions over your training set plus some model complexity penalty (regularization). -> single data set의 합, entire data set에 대한 것.

=> A loss function is a part of a cost function
-- 참고: https://stats.stackexchange.com/questions/179026/objective-function-cost-function-loss-function-are-they-the-same-thing