[BOJ][C#] 11403 경로 찾기

📕 문제

📌 링크

📗 접근 방식

생각한 풀이

한줄을 기준으로 탐색한다고 생각하고 한줄짜리 visited 배열을 선언하였다.

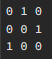
위 예제를 참고하여 설명하자면 첫번째 줄(0 1 0)을 탐색하면서 1인 인덱스를 찾고 방문처리를 해주면 해당 인덱스 행을 탐색하며 다시 1을 탐색한다.

다시 설명하면

1. 1행부터 n번째 행까지 전부 탐색을 할 것. 탐색시 방문처리를 위해 1차원 배열을 준비할 것.
2. 인덱스 값이 1일 때 해당 좌표(위 사진에서는 (1,2))를
   연결되어 있다고 표시,
   Queue에 넣기,
   방문처리하고 BFS처럼 탐색 시작
3. (1,2)가 들어갔기 때문에 2행을 확인
4. 2행에서는 (2,3)의 인덱스 값이 1이기 때문에
   연결되어 있다고 표시,
   Queue에 넣기,
   방문처리

위와 같은 방식으로 모든 행을 탐색한 결과를 새로운 2차원 배열에 기록하고 전부 탐색을 했다면 새로 기록한 2차원 배열을 출력한다.

플로이드-워셜 알고리즘

플로이드 - 워셜 알고리즘 [참고 링크1]
플로이드 - 워셜 알고리즘 [참고 링크2]

알고리즘 분류에 처음보는 알고리즘이 존재하여 해당 알고리즘을 검색 후 찾아보고 다른 사람들의 풀이를 참고하여 해당 알고리즘을 적용하여 제출해보았다.

📘 코드

1. 생각한 풀이 코드

namespace BOJ
{
    class No_11403
    {
        const int MAX = 102;

        static int n;
        static int[,] board = new int[MAX, MAX];
        static int[,] answer = new int[MAX, MAX];
        static bool[] visited = new bool[MAX];
        static Queue<(int, int)> q = new Queue<(int, int)>();

        static void Main()
        {
            n = int.Parse(Console.ReadLine());

            for(int i = 0 ; i < n ; i++)
            {
                int[] inputs = Array.ConvertAll(Console.ReadLine().Split(), int.Parse);
                for(int j = 0 ; j < n ; j++)
                {
                    board[i, j] = inputs[j];
                }
            }

            for(int i = 0 ; i < n ; i++)
            {
                for(int k = 0 ; k < n ; k++)
                    visited[k] = false;

                for(int j = 0 ; j < n ; j++)
                {
                    if(board[i, j] == 1)
                    {
                        q.Enqueue((i, j));
                        answer[i, j] = 1;

                        while(q.Count > 0)
                        {
                            var cur = q.Dequeue();
                            var curFrom = cur.Item1;
                            var curTo = cur.Item2;

                            for(int k = 0 ; k < n ; k++)
                            {
                                if(board[curTo, k] == 0) continue;
                                if(visited[k]) continue;

                                q.Enqueue((curTo, k));
                                visited[k] = true;
                                answer[i, k] = 1;
                            }
                        }
                    }
                }
            }

            for(int i = 0 ; i < n ; i++)
            {
                for(int j = 0 ; j < n ; j++)
                {
                    Console.Write($"{answer[i, j]} ");
                }
                Console.WriteLine();
            }
        }
    }
}

2. 플로이드-워셜 알고리즘 적용 코드

using System.Text;

namespace BOJ
{
    class No_11403
    {
        const int MAX = 102;
        const int INF = 987654321;

        static int n;
        static int[,] board = new int[MAX, MAX];

        static void Main()
        {
            StringBuilder sb = new StringBuilder();
            n = int.Parse(Console.ReadLine());

            for(int i=0 ;i<n ;i++)
            {
                int[] inputs = Array.ConvertAll(Console.ReadLine().Split(), int.Parse);
                for(int j=0 ;j<n ;j++)
                {
                    board[i, j] = inputs[j] == 0 ? INF : inputs[j];
                }
            }

            Floyd();

            for(int i = 0 ; i < n ; i++)
            {
                for(int j = 0 ; j < n ; j++)
                {
                    sb.Append(board[i, j] == INF ? "0 " : "1 ");
                }
                sb.Append('\n');
            }

            Console.WriteLine(sb.ToString());
        }

        static void Floyd()
        {
            for(int k = 0 ; k < n ; k++)
                for(int x = 0 ; x < n ; x++)
                    for(int y = 0 ; y < n ; y++)
                        if(board[x, y] > board[x, k] + board[k, y])
                            board[x, y] = board[x, k] + board[k, y];
        }
    }
}

📙 오답노트

📒 알고리즘 분류

• 그래프 이론
• 그래프 탐색
• 플로이드–워셜