[BOJ][C#] 1914 하노이 탑

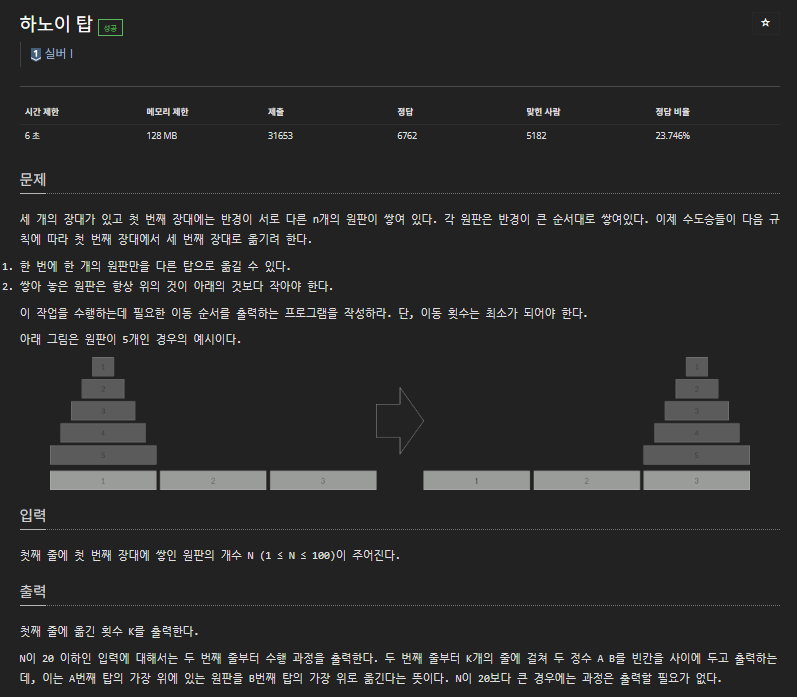
📕 문제

📌 링크

📗 접근 방식

하노이 탑 이동 횟수 계산:

• 이 탑 문제의 이동 횟수는 수학적인 규칙을 가지고 있습니다.
• 하노이 탑의 이동 횟수는 $2^n - 1$입니다.
• 따라서, BigInteger.Pow(2, n) - 1을 사용하여 이동 횟수를 계산합니다.
• n이 최대 100이므로 long타입으로 표현할 수 없기때문에 System.Numberics 네임스페이스의 BigInteger를 사용하였다.

이동 경로 출력:

• 이동 횟수가 20을 넘어갈 경우 전체 이동 경로를 출력하지 않고, 이동 횟수만 출력하고 종료한다.
• 이동 횟수가 20 이하일 경우, Hanoi 함수를 호출하여 하노이 탑의 이동 경로를 StringBuilder에 저장한다.
• Hanoi 함수는 재귀적으로 하노이 탑의 이동 경로를 계산하고, Move 함수를 호출하여 이동 경로를 출력한다.

결과 출력:

• 최종적으로 계산한 이동 횟수를 출력하고, 20 이하인 경우에는 하노이 탑의 이동 경로를 출력한다.

📘 코드

using System.Numerics;
using System.Text;

namespace BOJ
{
    class No_1914
    {
        static StringBuilder sb = new StringBuilder();
        
        static void Main()
        {
            int n = int.Parse(Console.ReadLine());

            BigInteger count = BigInteger.Pow(2, n) - 1;

            sb.AppendLine(count.ToString());

            if (n > 20)
            {
                Console.WriteLine(sb);
                return;
            }
            
            Hanoi(n, 1, 2, 3);
            
            Console.WriteLine(sb);
        }

        static void Move(int from, int to)
        {
            sb.AppendLine($"{from} {to}");
        }

        static void Hanoi(int n, int from, int by, int to)
        {
            if (n == 0) return;

            Hanoi(n - 1, from, to, by);
            Move(from, to);
            Hanoi(n - 1, by, from, to);
        }
    }   
}

📙 오답노트

📒 알고리즘 분류

• 임의 정밀도 / 큰 수 연산
• 재귀