📗깊이우선탐색(DFS):
그래프가 있을 때 그래프를 탐색하는 방법이 있을것이다. 깊이우선탐색은 시작노드에서부터 시작하여 그 시작노드의 하위 노드에 대한 탐색을 반복하고 더이상 하위노드가 존재하지 않을 때까지 이를 계속 반복한다.
모르는사람에게 이렇게 설명하면 😅 이런표정 나오기 쉽다.
그냥 깊은 터널에서 두가지 갈림길이 있다고 생각해보자.

어느 한 갈림길을 선택하였다면 그 끝까지 간다. 끝까지 갔더니 다른 한 갈림길도 궁금해졌다. 그 이전 갈림길로 돌아가 그 갈림길의 끝까지 간다. 이게 전부다.
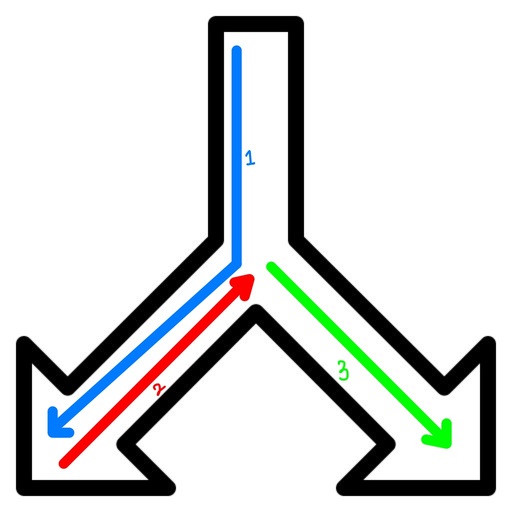
그림으로 살펴보면 먼저 1번 루트를 통해 끝까지 방문, 2번으로 되돌아와서 다시 3번방향으로 탐색한다.
(오른쪽 노드(갈림길), 왼쪽 노드(갈림길)의 방문 순서는 상관 없다)
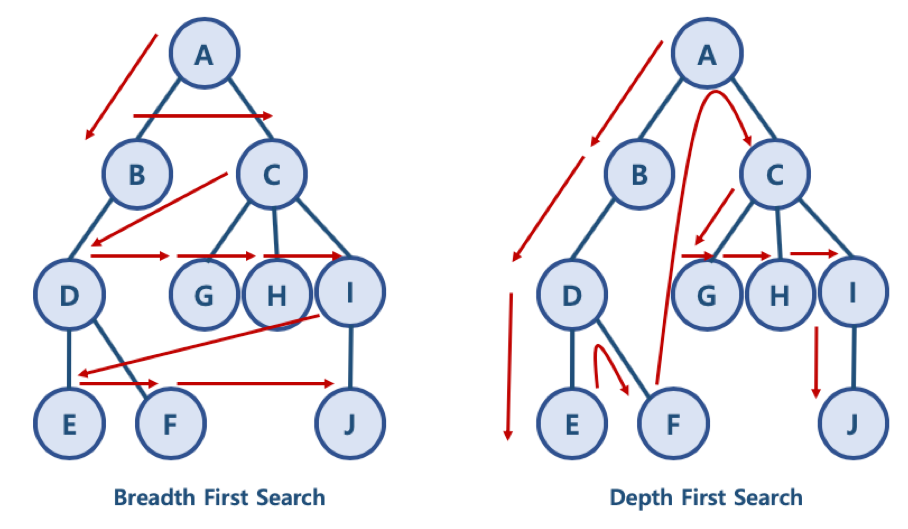
노드가 많아져도 앞서 살펴본 개념만 이해하면 쉽게 출력결과를 파악할 수 있다.
A를 시작노드로 할 때,
A->B->D->E->F->C->G->H->I->J로 방문할 것이다
(A->C->I->J->H->G->B->D->F->E도 가능)
DFS 구현 방법은 크게 재귀를 이용하는 방법, 스택을 이용하는 방법이 있다.
✏️ DFS 재귀 구현
graph = dict()
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
def dfs_recursive(graph, start, visited = []):
visited.append(start)
for node in graph[start]: #인접노드방문 ['A'] = ['B', 'C']일때 최소 2번
if node not in visited: # 방문을 하지 않았다면
dfs_recursive(graph, node, visited)#계속 반복
return visited
print(dfs_recursive(graph, 'A'))출력결과
['A', 'B', 'D', 'E', 'F', 'C', 'G', 'H', 'I', 'J']
재귀구현은 컴퓨터가 재귀함수를 반복적으로 호출한다. 그렇다면 호출된 함수는 운영체제가 관리하여 스택 메모리영역인 스택 프레임에 쌓는다. 스택프레임에 쌓인 함수들은 자기 안에서 호출된 가장 마지막 함수부터 수행하고 가장 마지막으로는 가장 먼저 불린 함수가 수행될 것이다.
✔️장점
DFS 알고리즘을 for문이나 while문으로 만들기 위해서는 스택 자료구조를 사용하면서 추가적인 변수 정보 등을 사용자가 추가로 관리해주어야 한다. 파이썬에서는 deque나 list를 사용할 것이다. 하지만 재귀로 구현을 한다면 스택메모리에 재귀적으로 호출된 함수들의 스택프레임이 만들어지고 변수 정보를 가지고 있으므로 신경쓰어야할 부분이 적어진다.
❌단점
함수가 함수를 호출하므로 스택영역에 스택프레임이 계속해서 생성된다. 스택오버플로우가 일어날 수 있어 주의해야한다.
✏️ DFS 스택 구현
from collections import deque
graph = dict()
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
def dfs(graph, start_node):
visited = []
need_visited = deque()
#while문 밖에서 시작 노드를 설정한다
need_visited.append(start_node)
## 방문이 필요한 배열이 아직 존재한다면 계속 반복
while need_visited:
## 방문이 필요한 배열에서 가장 마지막 노드 pop (==stack)
node = need_visited.pop()
# 방문하지 않았다면
if node not in visited:
## 현재 노드를 앞으로는 방문하지 못하도록 방문처리
visited.append(node)
## 그에 대한 인접 노드들은 방문이 필요할 수 있으므로 배열에 추가
need_visited.extend(graph[node])
return visited
print(dfs(graph, 'A'))출력결과
['A', 'C', 'I', 'J', 'H', 'G', 'B', 'D', 'F', 'E']
✔️장점
재귀호출에 비해 시간제약이 덜하다.
❌단점
재귀호출에 비해 가독성이 떨어질 수 있다.
⚠️주의
Iterative하게 구현했을때 재귀와 방문순서가 다르게 출력된다.
📗너비우선탐색(BFS):
너비우선탐색은 루트노드에서 가장 가까운 거리에 있는 노드 순서로 탐색하는 알고리즘이다. 고층 빌딩을 청소한다고 할때 가장 최적의 움직임으로 청소를 하려면 어떻게 해야할까? 루프를 타고 내려올때 가장 넓은 범위까지 접근한 뒤 내려오는것이다. 넓게 탐색한다고 생각하면 편하다. 루트노드에서 가장 멀리 떨어진 노드를 가장 마지막에 방문한다.

A를 시작노드로 할 때, A->B->C->D->G->H->I->E->F->J로 방문한다.
✏️ BFS 큐 구현
from collections import deque
graph = dict()
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
def bfs(graph, start_node):
visited = []
need_visited = deque()
#while문 밖에서 시작 노드를 설정한다
need_visited.append(start_node)
## 방문이 필요한 배열이 아직 존재한다면 계속 반복
while need_visited:
## 방문이 필요한 배열에서 가장 처음 노드 pop (==queue)
node = need_visited.popleft()
# 방문하지 않았다면
if node not in visited:
## 현재 노드를 앞으로는 방문하지 못하도록 방문처리
visited.append(node)
## 그에 대한 인접 노드들은 방문이 필요할 수 있으므로 배열에 추가
need_visited.extend(graph[node])
return visited
print(bfs(graph, 'A'))출력결과
['A', 'B', 'C', 'D', 'G', 'H', 'I', 'E', 'F', 'J']
사실상 node = need_visited.pop()줄을 node = need_visited.popleft()로 고쳐만 주면 BFS코드가 된다.
최종정리 DFS, BFS 장단점
DFS
✔️장점
내가 찾고자 하는 목표 노드가 깊이 있는 곳에 존재하는 경우 BFS 보다 빠르게 탐색이 가능하다.
❌단점
목표에 이르는 경로가 다수일 때, DFS가 목표 노드에 도착하면 탐색을 종료하기 때문에 그 목표노드가 최단경로라는 보장을 하지 못한다.
BFS
✔️장점
그래프의 노드의 수가 적고 찾고자 하는 목표노드가 깊이가 얕은곳에 존재할 때 빠르게 동작할 수 있다.
모든 경로를 탐색하기때문에 답이 되는 경로가 여러 개인 경우 최단 경로임을 보장한다.
❌단점
최악의 경우 모든 노드를 탐색해야 하기 때문에 큰 공간을 필요로하고, 깊이 있는 곳에 목표노드가 있을 시 오랜시간이 소요된다.
🔎 참고
https://geniusnohkang.tistory.com/28
https://data-marketing-bk.tistory.com/44
https://veggie-garden.tistory.com/42
