
가중치 벌칙
규제 : 학습 모델이 훈련집합의 예측을 너무 잘 수행하지 못하도록 방지
+ 규제항은 훈련집합과 무관하며, 데이터 생성 과정에 내재한 사전 지식에 해당
+ 규제항은 매개변수를 작은 값으로 유지하여 모델의 용량(capacity)을 제한하는 역할(수치적 용량 크기 제한함)
-> 큰 가중치에 벌칙을 가해 작은 가중치를 유지하려고 주로 L2 Norm이나 L1 Norm을 사용
A regularizer is an additional criteria to the loss function to make sure that we don't overfit
It's called a regularizer sinde it tries to keep the parameters more normal/regular
It is a bias on the model forces the learning to prefer certain types of weights over others

Regularizaion term을 추가함으로 곡률이 바뀜(추가) -> overfitting을 극복
- Generally, we don't wand hube weights
- If weights are large, a small change in a feature can result in a large change in the prediction
- Might also prefer weights of 0 for features that aren't useful
=> Weight 값의 크기에 대한 규제
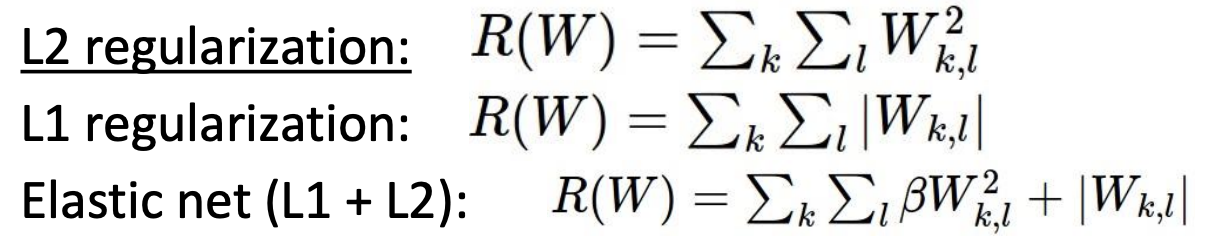
Reguliarization은 정규화라는 의미보다는 제약을 주는 것이라 기억하자!
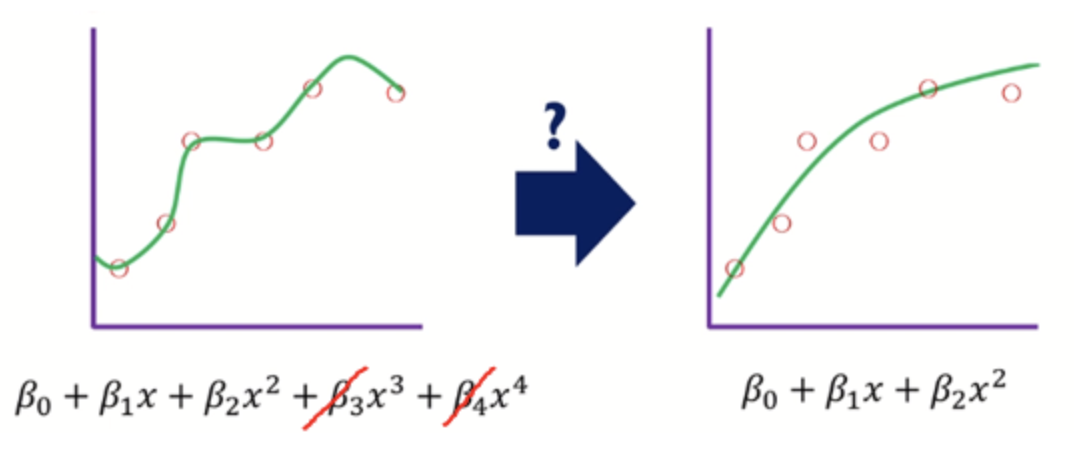
왼쪽의 그림 : high variance, low bias -> overfitting
일반화를 위해서 오른쪽의 그림처럼 완화시켜주어야 한다!
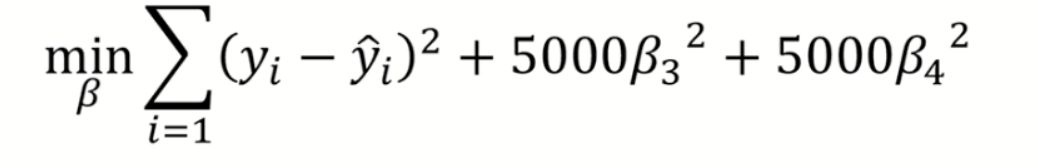
위의 손실함수 식에서 최적의 weight가 되기 위해서(손실함수가 0으로 수렴하기 위해서)는 B3, B4가 0가 가까워 져야 한다. 이렇게 B3과 B4의 영향력을 감소시켜줌으로 모델을 단순화 할 수 있고 이런 식으로 penalize, 즉 weight에 패널티를 줌으로 overfitting을 방지한다.
방법으로는 3가지 방법이 있다.
- L1 Norm(절대값)
- L2 Norm(제곱)
- Elastic Net(L1 + L2)
If W is positive, reduces W
If W is negative, increases W
L1은 절대값으로 gradient descent에서 weight 미분 시 weight의 부호만 남게 되어, weight의 크기(magnitude)에 상관 없이 constant하게 0으로 향한다.
L2는 제곱값으로 gradient descent에서 weight 미분 시 weight의 부호와 함께 크기도 남으므로, weight의 몸집에 따라 0으로 향한다.
일반적으로 NN에서는 L2를 사용한다.
