MaxHeap (Python)

Heap은 이진트리의 한 종류이며, 정렬시에 유용하게 사용됨

Heap

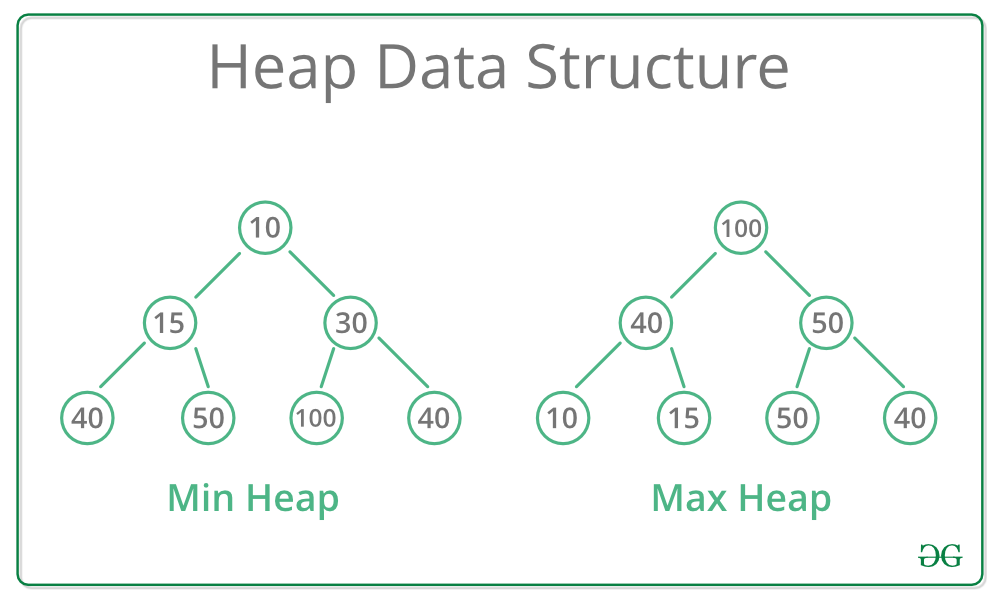
• BinaryTree의 한종류이며, 완전 이진트리의 구조를 가지고 있음

• 루트 노드가 언제나 최대 혹은 최소 값을 가짐. (MaxHeap, MinHeap)
• 서브트리도 모드 Heap 구조
• 자식 노드들 간의 관계는 이진탐색트리와 다르게 상관 없음
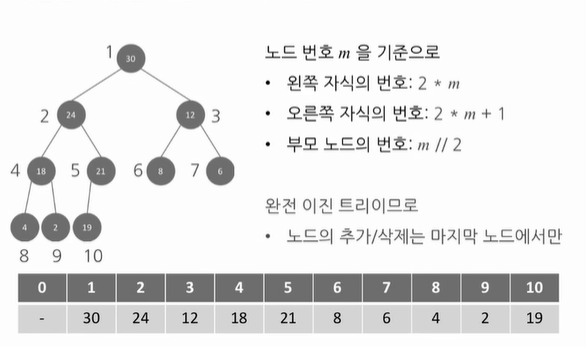
• 루트 노드는 1번으로 시작하며, 어레이 형식으로 담기에 편함 (왼쪽자식 2i, 오른쪽 자식 2m + 1
  

구현 및 시간복잡도

class MaxHeap:

    def __init__(self):
        self.data = [None]

1) 원소 삽입: insert()

트리의 마지막 인덱스에 새로운 원소를 임시 저장하고 부모노드와의 비교를 통해 위로 이동.

시간복잡도 : O(logN) - 부모노드와 대소 비교 횟수

def insert(self, item):
    self.data.append(item)
    idx = len(self.data) - 1
    while idx > 1:
        if self.data[idx] > self.data[idx//2]:
            self.data[idx], self.data[idx//2] = self.data[idx//2], self.data[idx]
            idx = idx//2
        else:
            break

2)원소의 삭제

루트 노드의 제거(Max Heap일 경우 최대값)
트리 마지막 인덱스의 Key 값을 루트 노드로 이동 후, Left Right 자식들과 비교하며 자리를 바꿈. (Left Right 중 더 큰 값과 교체)

시간복잡도 : O(logN) - 자식 노드와 대소 비교 횟수

def remove(self):
    if len(self.data) > 1:
        self.data[1], self.data[-1] = self.data[-1], self.data[1]
        data = self.data.pop(-1)
        self.maxHeapify(1)
    else:
        data = None
    return data

def maxHeapify(self, i):
    left = i * 2
    right = i * 2 + 1
    smallest = i
    if left < len(self.data) and self.data[left] > self.data[smallest]:
        smallest = left
    if right < len(self.data) and self.data[right] > self.data[smallest]:
        smallest = right

    if smallest != i:
        self.data[i], self.data[smallest] = self.data[smallest] = self.data[i]
        self.maxHeapify(smallest)

3) 활용방안

• Priority Que (Dequeue에서 최대 혹은 최소값 반환: O(logN)
• HeapSort