08-1. 트리의 개요
비선형 자료구조
트리(Tree)의 접근
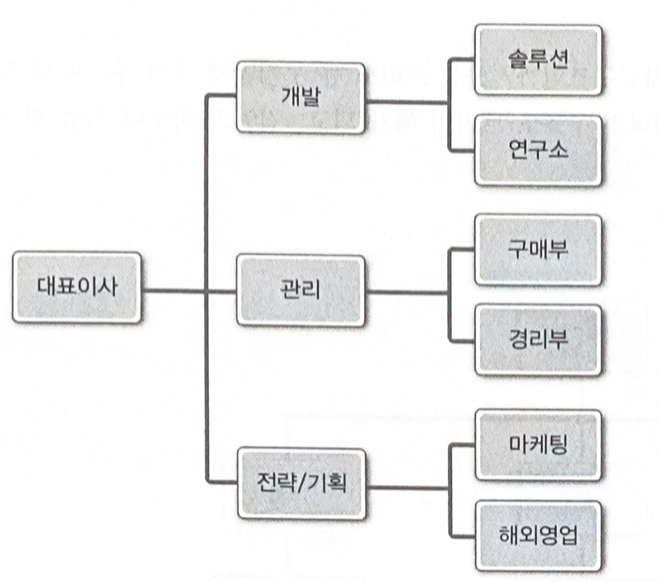
트리는 계층적 관계를 표현하는 자료구조이다
트리가 표현할 수 있는 것들
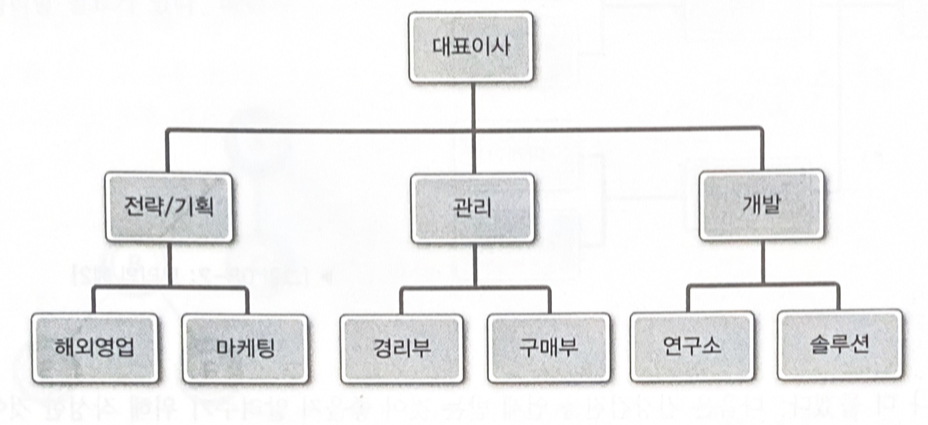
가지를 늘려가며 뻗어나간다
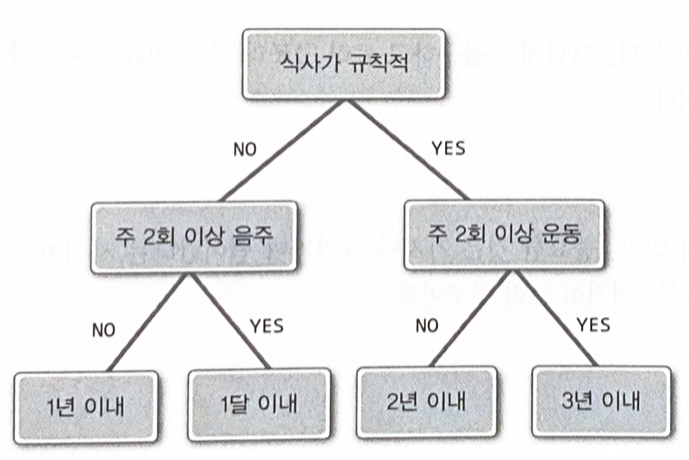
[의사 결정 트리]
트리 관련 용어의 소개
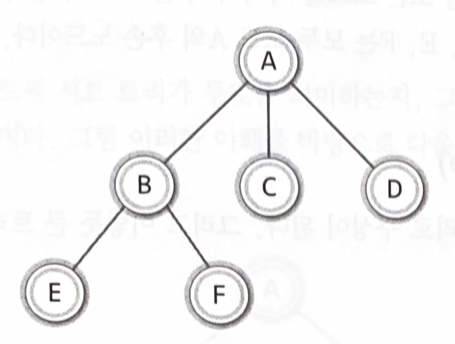
- 노드 : node
트리의 구성요소에 해당하는 A, B, C, D, E와 같은 요소 - 간선 : edge
노드와 노드를 연결하는 연결선 - 루트 노드 : root node
트리 구조에서 최상위에 존재하는 A와 같은 노드 - 단말 노드 : terminal node
아래로 또 다른 노드가 연결되어 있지 않은 C, D, E, F와 같은 노드 - 내부 노드 : internal node
단말 노드를 제외한 노드로 A, B와 같은 노드
단말 노드는 잎사귀 노드(leaf node) 라고도 불리며,
내부 노드는 단말 노드가 아니라고 하여 비단말 노드(noninternal node) 라고도 불린다
- 노드 A는 노드 B, C, D의 부모 노드(parent node)이다
- 노드 B, C, D는 노드 A의 자식 노드(child node)이다
- 노드 B, C, D는 부모가 같으므로, 서로가 서로에게 형제 노드(sibling node)이다
- 조상노드(Ancestor node)
특정 노드의 위에 위치하는 모든 노드 - 후손 노드(Descendent node)
특정 노드의 아래에 위치하는 모든 노드
이진 트리와 서브 트리
- 서브트리
큰 트리에 속하는 작은 트리
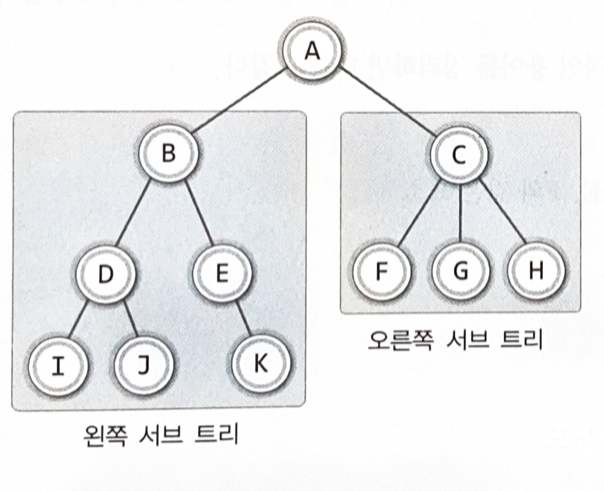
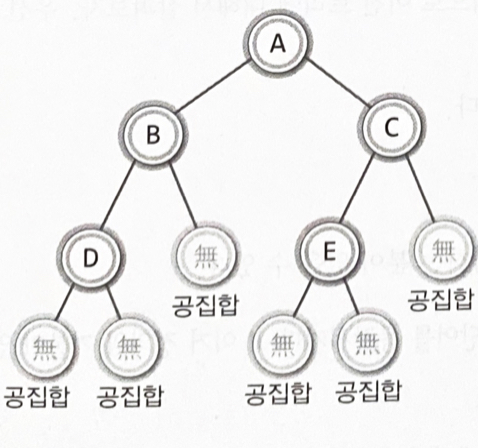
- 이진 트리(binary tree)
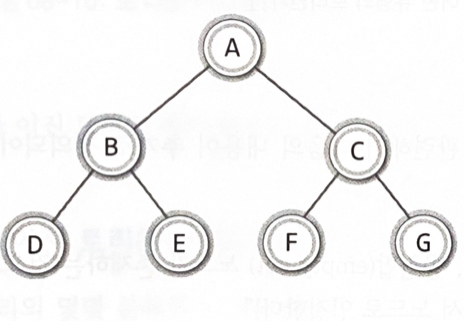
- 루트 노드를 중심으로 두 개의 서브트리로 나뉘어진다
- 나뉘어진 두 서브 트리도 모두 이진트리이다
Ex)
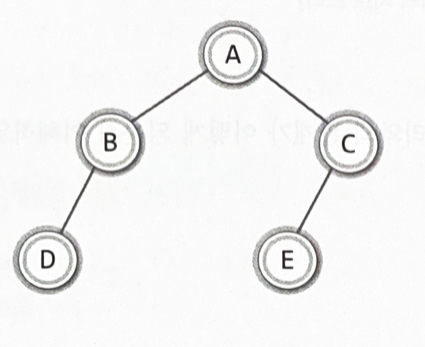
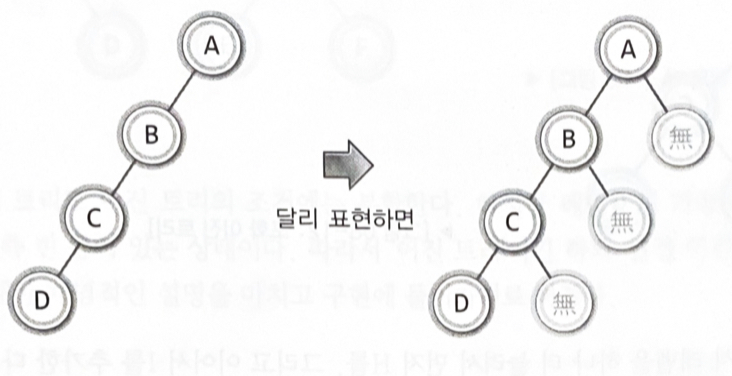
공집합(empty node)노드는 이진트리의 판단에 있어서 노드로 인정한다
포화 이진 트리(Full Binary Tree)와 완전 이진 트리(Complete Binary Tree)
- 레벨 : 층별로 숫자를 매긴 것
- 높이 : 트리의 최고 레벨

- 포화 이진 트리 : 모든 레벨이 꽉 차있어서 노드를 더 추가하려면 레벨을 높여야 한다
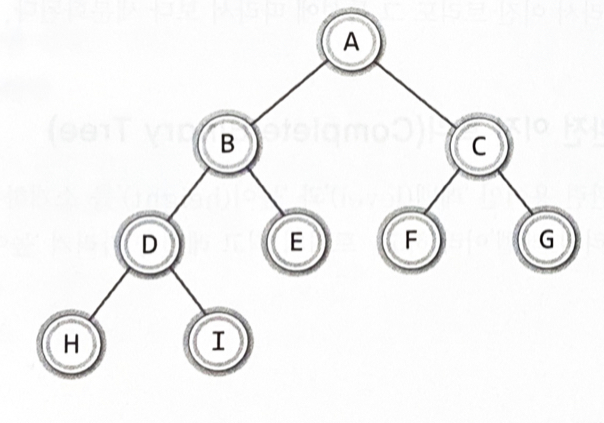
- 완전 이진 트리 : 포화 이진 트리처럼 모든 레벨이 꽉 차있는 것은 아니지만, 빈 틈 없이 노드가 채워진 이진 트리
위에서 아래로, 왼쪽에서 오른쪽의 순서대로 채워진다
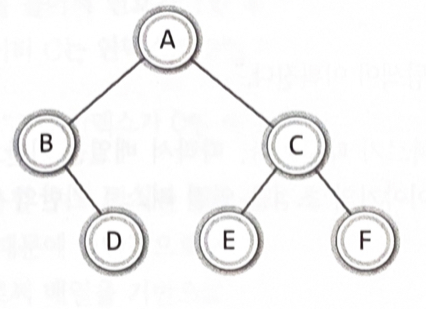
- 그냥 이진 트리
08-2. 이진 트리의 구현
이진 트리의 구현 방법 : 배열 or 연결리스트
트리를 표현하기에는 연결 리스트가 더 유연하다
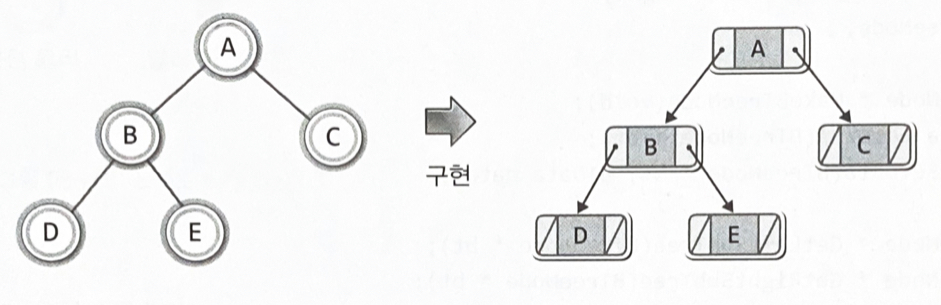
하지만 트리가 완성된 이후 매우 빈번한 탐색이 이루어지는 트리일 경우 배열로 구현한다. 탐색이 매우 용이하고 빠르기 때문이다
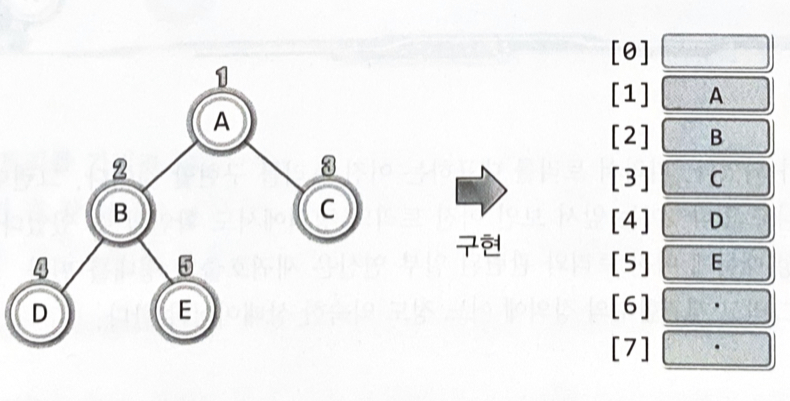
헤더파일에 정의된 구조체의 이해
#ifndef __BINARY_TREE_H__
#define __BINARY_TREE_H__
typedef int BData;
typedef struct _bTreeNode
{
BTdata data;
struct _bTreeNode * left;
struct _bTreeNode * right;
} BTreeNode;
BTreeNode * MakeBTreeNode(void);
BTData GetData(BTreeNode *bt);
void SetData(BTreeNode *bt, BTData data);
BTreeNode * GetLeftSubTree(BTreeNode * bt);
BTreeNode * GetRightSubTree(BTreeNode * bt);
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);
#endif헤더파일에 선언된 함수들의 기능
BTreeNode * MakeBTreeNode(void);: 노드의 생성BTData GetData(BTreeNode * bt);: 노드에 저장된 데이터를 반환void SetData(BTreeNode * bt, BTData data);: 노드에 데이터를 저장BTreeNode * GetLeftSubTree(BTreeNode * bt);: 왼쪽 서브 트리 주소 값 반환BTreeNode * GetRightSubTree(BTreeNode * bt);: 오른쪽 서브 트리 주소 값 반환
이진 트리 자료구조의 ADT
BTreeNode * MakeBTreeNode(void);
- 이진 트리 노드를 생성하여 그 주소 값을 반환한다
BTData GetData(BTreeNode * bt);
- 노드에 저장된 데이터를 반환한다
void SetData(BTreeNode * bt, BTData data);
- 노드에 데이터를 저장한다. Data로 전달된 값을 저장한다
BTreeNode * GetLeftSubTree(BTreeNode * bt);
- 왼쪽 서브 트리의 주소 값을 반환한다
BTreeNode * GetRightSubTree(BTreeNode * bt);
- 오른쪽 서브 트리의 주소 값을 반환한다
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub);
- 왼쪽 서브 트리를 연결한다
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub);
- 오른쪽 서브 트리를 연결한다
이진 트리의 구현
#include <stdio.h>
#include <stdlib.h>
#include "BinaryTree.h"
BTreeNode * MakeBTreeNode(void)
{
BTreeNode *nd = (BTreeNode*)malloc(sizeof(BTreeNode));
nd->left = NULL;
nd->right = NULL;
return nd;
}
BTData GetData(BTreeNode * bt)
{
return bt->data;
}
void SetData(BTreeNode * bt, BTData data)
{
bt->data = data;
}
BTreeNode * GetLeftSubTree(BTreeNode * bt)
{
return bt->left;
}
BTreeNode * GetRightSubTree(BTreeNode * bt)
{
return bt->right;
}
void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->left != NULL)
free(main->left);
main->left = sub;
}
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub)
{
if(main->right != NULL)
free(main->right);
main->right = sub;
}08-3. 이진 트리의 순회(Traversal)
순회의 세 가지 방법
- 전위 순회(Preorder Traversal) : 루트 노드를 먼저
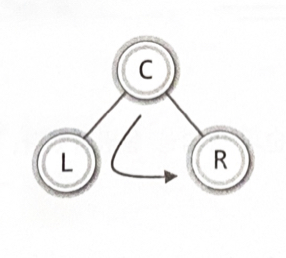
- 중위 순회(Inorder Traversal) : 루트 노드를 중간에

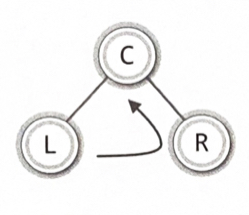
- 후위 순회(Postorder Traversal) : 루트 노드를 마지막에
순회의 재귀적 표현
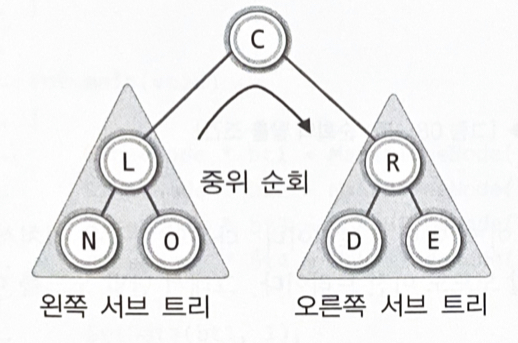
- 1단계 : 왼쪽 서브 트리의 순회
- 2단계 : 루트 노드의 방문
- 3단계 : 오른쪽 서브 트리의 순회
void InorderTraverse(BTreeNode * bt) // 이진 트리 전체를 중위 순회하는 함수
{
InorderTraverse(bt->left); // 1단계 왼쪽 서브 트리의 순회
printf(“%d \n”, bt->data); // 2단계 루트 노드의 방문
InorderTraverse(bt->right); // 3단계 오른쪽 서브 트리의 순회
}재귀의 탈출 조건이 정의되어 있지 않다
노드의 방문이 그저 데이터의 출력이다
재귀의 탈출 조건
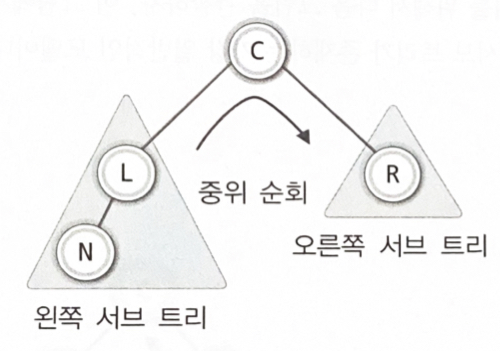
- 1단계 : 왼쪽 서브 트리의 순회 (노드N)
- 2단계 : 루트 노드의 방문 (노드L)
- 3단계 : 오른쪽 서브 트리의 순회 (공집합노드)
void InorderTraverse(BTreeNode * bt) // 이진 트리 전체를 중위 순회하는 함수
{
if(bt == NULL) // bt가 NULL이면 재귀 탈출!
return;
InorderTraverse(bt->left); // 1단계 왼쪽 서브 트리의 순회
printf(“%d \n”, bt->data); // 2단계 루트 노드의 방문
InorderTraverse(bt->right); // 3단계 오른쪽 서브 트리의 순회
}
전위 순회
void PreorderTraverse(BTreeNode * bt)
{
if(bt == NULL)
return;
printf(“%d \n”, bt->data); // 전위 순회이므로 루트 노드 먼저 방문
PreorderTraverse(bt->left);
PreorderTraverse(bt->right);
}후위 순회
void PostorderTraverse(BTreeNode * bt)
{
if(bt == NULL)
return;
PostorderTraverse(bt->left);
PostorderTraverse(bt->right);
printf(“%d \n”, bt->data); // 후위 순회이므로 루트 노드 나중에 방문!
}08-4. 수식 트리(Expression Tree)의 구현

루트 노드에 저장된 연산자의 연산을 하되, 두 개의 자식 노드에 저장된 두 피연산자를 대상으로 연산을 한다
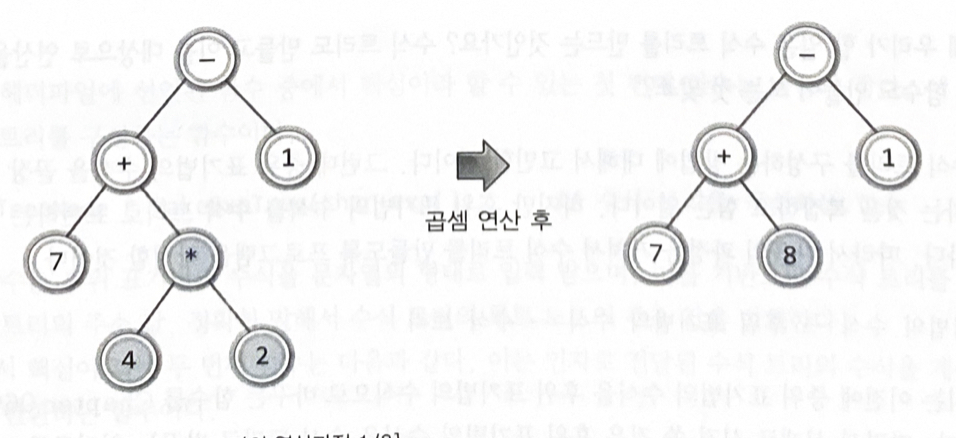
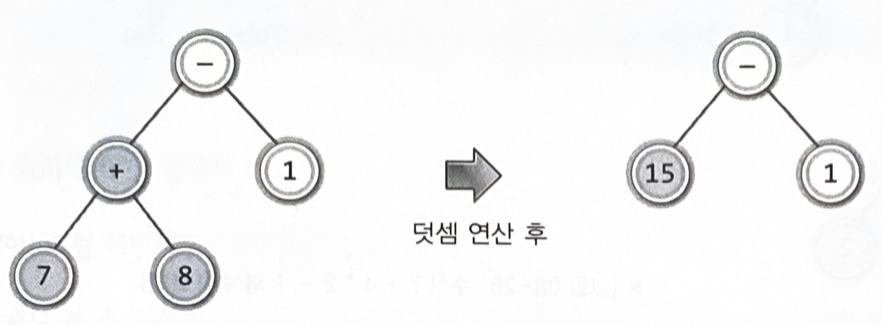
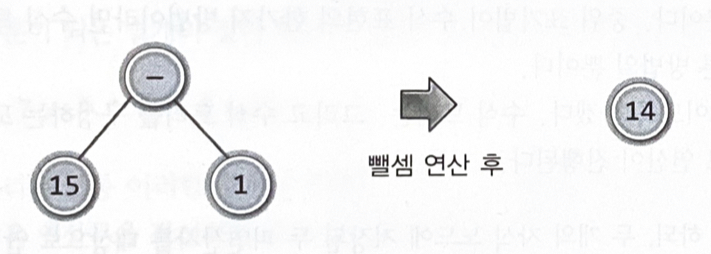
중위 표기법의 수식 -> 후위 표기법의 수식 -> 수식 트리
수식 트리의 구현에 필요한 도구와 헤더파일의 정의
#ifndef __EXPRESSION_TREE_H__
#define __EXPRESSION_TREE_H__
#include "BinaryTree2.h"
BTreeNode * MakeExpTree(char exp[]); // 수식 트리 구성
int EvaluateExpTree(BTreeNode * bt); // 수식 트리 계산
void ShowPrefixTypeExp(BTreeNode * bt); //전위 표기법 기반 출력
void ShowInfixTypeExp(BTreeNode * bt); // 중위 표기법 기반 출력
void ShowPostfixTypeExp(BTreeNode * bt); //후위 표기법 기반 출력
#endif후위 표기법
- 왼쪽에서 오른쪽으로 연산자가 나열된다
- 두 피연산자는 연산자 앞에 나열된다



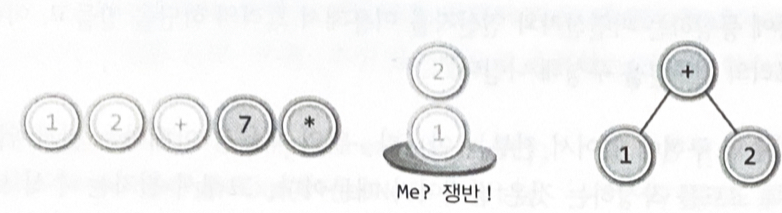
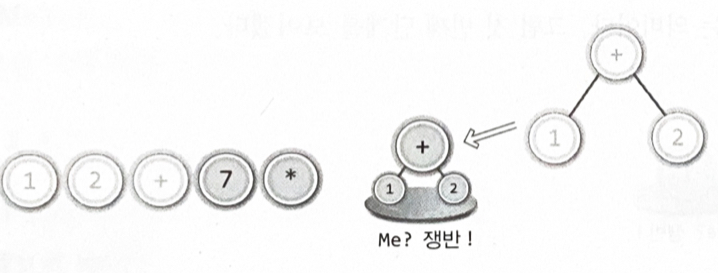

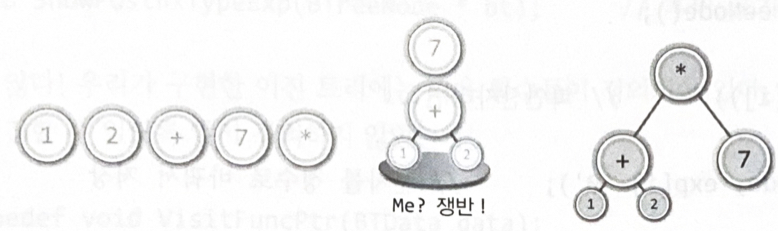
수식트리를 구성하는 방법
- 피연산자를 만나면 무조건 스택으로 옮긴다
- 연산자를 만나면 스택에서 두 개의 피연산자를 꺼내어 자식 노드로 연결한다
- 자식 노드를 연결해서 만들어진 트리는 다시 스택으로 옮긴다
BTreeNode * MakeExpTree(char exp[])
{
Stack stack;
BTreeNode * pnode;
int expLen = strlen(exp);
int i;
StackInit(&stack);
for(i = 0; i < expLen; i++)
{
pnode = MakeBTreeNode();
if(isdigit(exp[i])) // 피연산자라면 ...
{
SetData(pnode, exp[i]-'0'); //문자를 정수로 바꿔서 저장
}
else // 연산자라면...
{
MakeRightSubTree(pnode, SPop(&stack));
MakeLeftSubTree(pnode, SPop(&stack));
SetData(pnode, exp[i]);
}
SPush(&stack, pnode);
}
return SPop(&stack);
}수식 트리의 순회
- 전위 순회하여 데이터를 출력한 결과 : 전위 표기법의 수식
- 중위 순회하여 데이터를 출력한 결과 : 중위 표기법의 수식
- 후위 순회하여 데이터를 출력한 결과 : 후위 표기법의 수식
void ShowPrefixTypeExp(BTreeNode * bt) // 전위 표기법의 수식으로
{
PreorderTraverse(bt, ShowNodeData);
}void ShowInfixTypeExp(BTreeNode * bt) // 중위 표기법의 수식으로
{
InorderTraverse(bt, ShowNodeData);
}void ShowPostfixTypeExp(BTreeNode * bt) // 후위 표기법의 수식으로
{
PostorderTraverse(bt, ShowNodeData);
}수식 트리의 계산
int EvaluateExpTree(BTreeNode * bt)
{
int op1, op2;
if(GetLeftSubTree(bt) == NULL && GetRightSubTree(bt) == NULL) // 단말 노드라면
return GetData(bt);
op1 = GetData(GetLeftSubTree(bt)); // 첫 번째 피연산자
op2 = GetData(GetRightSubTree(bt)); // 두 번째 피연산자
switch(GetData(bt)) // 연산자를 확인하여 연산을 진행
{
case ‘+’ :
return op1+op2;
case ‘-‘ :
return op1-op2;
case ‘*’ :
return op1*op2;
case ‘/‘ :
return op1/op2;
}
return 0;
}