2xn 타일링

시간 제한	메모리 제한	제출	정답	맞힌 사람	정답 비율
1 초	256 MB	105065	39690	29038	35.517%

문제

2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.

아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.

입력

첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)

출력

첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.

예제 입력 1

2

예제 출력 1

2

예제 입력 2

9

예제 출력 2

55

코드

import java.io.*;

public class P_11726 {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int n = Integer.parseInt(br.readLine());
        int[] rectangle = new int[1001];

        rectangle[1] = 1;
        rectangle[2] = 2;
        for (int i = 3; i <= n; i++) rectangle[i] = (rectangle[i - 1] + rectangle[i - 2]) % 10007;

        bw.write(Integer.toString(rectangle[n]));
        bw.flush();
    }
}

코드 설명

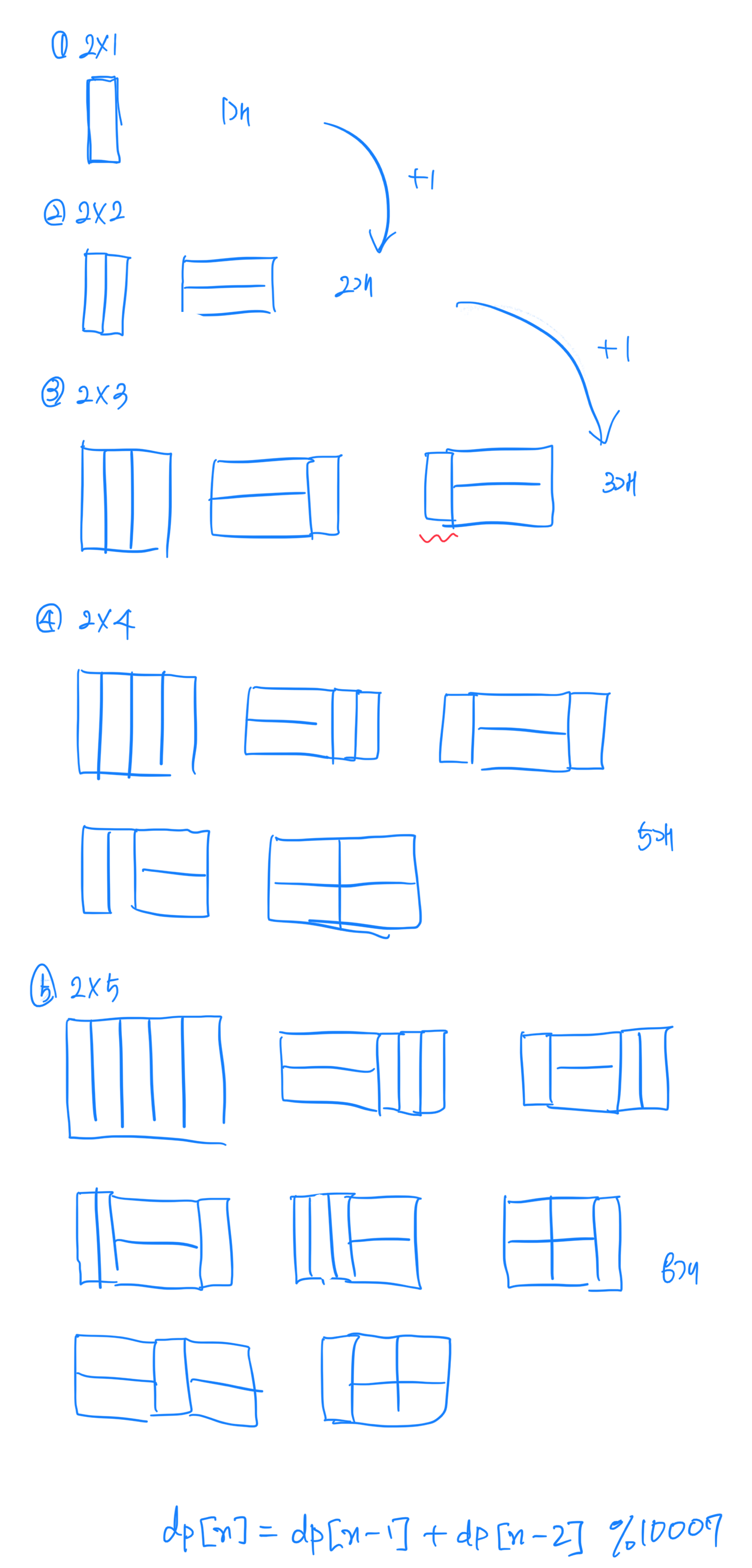
dp[n]은 2xn 타일의 직사각형을 채울 수 있는 최대 방법 수이다.
문제에서 제시된 타일 조각은 1x2와 2x1뿐이다.

그럼 dp[n]은 dp[n-1]의 조각들에 2x1 조각을 추가한 방법 수에 d[n-2]의 조각들에 1x2조각 두 개를 추가한 방법 수를 더한 것이라고 할 수 있다.