[DL] Error Back Propagation

Kyeongmin·2023년 10월 28일
인공지능
0

인공지능

목록 보기
1/9

이 글에서는 인공지능에 대해 공부하며 배웠던 것들에 대해서 정리하는 글입니다.

배경

Error Back Propagation은 Neural Network의 학습에 사용되는 학습 알고리즘이며,
기존의 Gradient Descent Method를 활용한 기법이다.

처음 Neural Network 구조가 제안되었을때 실제 문제에 활용할 수 없었는데,
바로 학습 알고리즘이 없어 Neural Network의 Weight를 계산할 수 없었기 때문이다.

Error Back Propagation에 대한 본격적인 설명에 앞서,
Neural Network의 학습과 Gradient Descent Method에 대해 간단히 알아보자.

Neural Network(신경망)의 학습

Neural Network을 포함한 대부분의 인공지능 모델의 목적은 모두 동일하다.
주어진 X를 가지고 실제 Y와 유사한 값을 예측하기 위함인데,
Neural Network은 Weight 값의 조정을 통해 주어진 X를 통해 예측값 Y'를 산출한다.

즉 Neural Network의 학습은 실제값 Y와 예측값 Y' 사이의 오차를 최소화하는 Weight 값을 찾아내는 과정이라고 말할 수 있다.

학습 과정을 수식으로 표현하면 아래와 같다.
Find weights w=(w1,w2, ⋯ wn)\textbf{w} = (w_1,w_2,\,\cdots\,w_n) so that NN(w,x) = yNN(\textbf{w},\textbf{x})\,=\,\textbf{y} for all (x,y)(\textbf{x},\textbf{y})

다만 예측값과 실제값이 완전히 같을 수 없기 때문에,
Neural Network은 둘 사이의 오차를 최소화하는 것을 목적으로 학습을 진행한다.
이를 다시 수식으로 표현하자면 아래와 같다.

minimizeE(w)  =  ∑(x,y)∈all  (y  −  NN(w,x))2minimize\quad\textbf{E}(\textbf{w})\;=\; \sum\limits_{(x,y)\in all}\;(\textbf{y}\;-\;NN(\textbf{w},\textbf{x}))^2

Gradient Descent Method (경사하강법)

그렇다면 E(w)\textbf{E}(\textbf{w}) 최소화되는 지점은 어디일까?
E\textbf{E} 를 w\textbf{w} 에 대해 미분했을 때 0이 되는 지점이라고 추정할 수 있다.

이러한 관점을 활용하는 것이 Gradient Descent Method 라고 할 수 있는데,
미분값(기울기)가 0이 되는 지점을으로 w\textbf{w} 값을 이동시키는 방식이다.

아래 수식을 통해 더 이상 이동할 지점이 없거나(미분값 0) 이동값이 작아질때까지 반복하여 최소화 되는 지점을 찾아내는 것이다.

wt+1  =  wt  −  η∂E∂ww^{t+1}\;=\;w^{t}\;-\;\eta\frac{\partial E}{\partial w}

※ η\eta (learning late, 학습률) : 구해진 기울기를 통해 어느정도 이동할 것인지 결정하는 Parameter

Error Back Propagation

자 이제 본격적으로 Neural Network 에서 Error Back Propagation(이하 EBP)이 어떤식으로 작동하는지 알아보자.

간단한 구조를 가진 Neural Network 가 있다고 가정해보자. (a1,a2a^1,a^2는 Activation Function의 결과값)

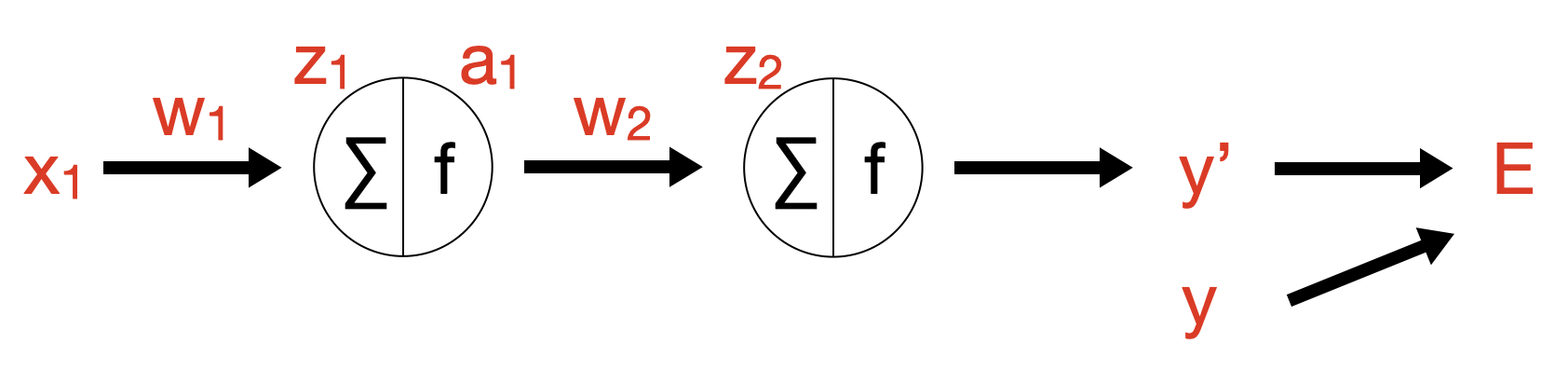
기울기 연산

① 각 항목별 수식은 아래와 같다.

z1  =  x1w1a1  =  sigmoid(z1)z2  =  a1w2y′  =  sigmoid(z2)E  =  ∑12(y−y′)2\begin{aligned} z_1\;&=\;x_1w_1 \\ a_1\;&=\;sigmoid(z_1) \\ z_2\;&=\;a_1w_2 \\ y^{\prime}\;&=\;sigmoid(z_2) \\ \textbf{E}\;&=\;\sum\frac{1}{2}(y-y\prime)^2 \end{aligned}

② 그렇다면 아래와 같이 편미분을 통해 w1,w2w_1, w_2 항목에 대해 기울기를 구할 수 있다.

∂E∂w2  =  ∂E∂y′∂y′∂z2∂z2∂w2=(y−y′)×y′(1−y′)×a1  ∂E∂w1  =  ∂E∂y′∂y′∂z2∂z2∂a1∂a1∂z1∂z1∂w1  =  (y−y′)×y′(1−y′)×w2×a1(1−a1)×x1\begin{aligned} \frac{\partial \textbf{E}}{\partial w_2}\;&=\; \frac{\partial \textbf{E}}{\partial y\prime} \frac{\partial y\prime}{\partial z_2} \frac{\partial z_2}{\partial w_2} = (y-y\prime) \times y\prime(1-y\prime) \times a_1 \\\;\\ \frac{\partial \textbf{E}}{\partial w_1}\;&=\; \frac{\partial \textbf{E}}{\partial y\prime} \frac{\partial y\prime}{\partial z_2} \frac{\partial z_2}{\partial a_1} \frac{\partial a_1}{\partial z_1} \frac{\partial z_1}{\partial w_1} \\\;\\ &=\;(y-y\prime) \times y\prime(1-y\prime) \times w_2 \times a_1(1-a_1) \times x_1 \end{aligned}

③ 구해진 도함수를 통해 기울기를 알 수 있고, 오차를 최소화하는 방향으로 weight를 이동시킬 수 있다.

w2t+1  =  w2−η∂E∂w2  w1t+1  =  w1−η∂E∂w1\begin{aligned} w^{t+1}_{2}\;&=\;w_2-\eta\frac{\partial\textbf{E}}{\partial w_2} \\\;\\ w^{t+1}_{1}\;&=\;w_1-\eta\frac{\partial\textbf{E}}{\partial w_1} \end{aligned}

⓸ 위 과정을 반복하면 오차를 최소화하는 w\textbf{w} 를 구할 수 있다.

연산 최적화

  1. back propagation 방법
  2. 연산량 최적화 방법 ... 공통 수식을 활용한

단점

위와 같이 GD(gradient descent)를 이용한 EBP의 계산 방식에는 단점이 있다. 바로 연산량이다.
Back propagation으로 연산량을 줄였지만, weight를 1번 업데이트 하기 위해서는 모든 데이터에 대한 오차를 구해야한다.

최적점(minima)에 도달하기 위해서는 무수히 많은 업데이트를 해야하는데,
업데이트 때마다 모든 데이터에 대한 오차를 계산하게 되면 연산량이 커지고 시간이 오래 걸린다는 단점 때문에 SGD(stochastic gradient descent)라는 기법을 활용하기도 한다.

기회가 된다면 다음에 SGD에 대해서도 다뤄보겠다.

profile
Kyeongmin
개발자가 되고 싶은 공장장이🛠
다음 포스트

[DL] Regression and Classification

0개의 댓글