자료구조 #7 트리(Tree)

Kyeongmin·2025년 5월 8일

대학원

목록 보기

34/34

이 글은 이소연 교수님의 자료구조 강의를 듣고 정리한 내용입니다.

먼저 Tree는 우리 주변에서 굉장히 많이 사용되는 자료구조로써 흔히 회사에서 조직도를 표현할때, 나라-지방-시 형태의 주소를 표현하거나 컴파일러에서도 사용되는 굉장히 중요한 자료구조이다.
이번 글에서는 Tree가 무엇인지에서부터 어떻게 활용할 수 있는지에 대해서 다뤄보고자 한다.

트리(Tree)란?

트리(Tree)는 비선형 자료구조의 하나로써, 연속적인 데이터가 아닌 계층적인 구조를 가진 데이터를 저장할때 주로 사용되는 자료구조이다. 트리는 이름에서처럼 알 수 있듯이 나무처럼 뿌리에서 시작해서 가지가 갈라지는 형태를 지니는데, 자료구조에서는 뿌리가 위에 있고 가지들이 아래로 뻗어 나가는 거꾸로 된 나무의 형태로 표현하며 우리 주변에서는 아래 그림과 같이 조직도를 나타낼때나 파일 시스템을 구성할때에 많이 사용되는 것을 알 수 있다.

1️⃣ 트리의 정의

트리는 기본적으로 1개 이상의 Node를 갖는 집합으로, Node는 다음과 같은 특징을 지닌다.

1개의 Root Node를 가지고 있다.
Root Node에는 N개의 Subtree가 존재할 수 있고, Subtree 간에 중복되는 Node는 없다.
트리에는 Cycle이 없는 Acyclic Graph이다.

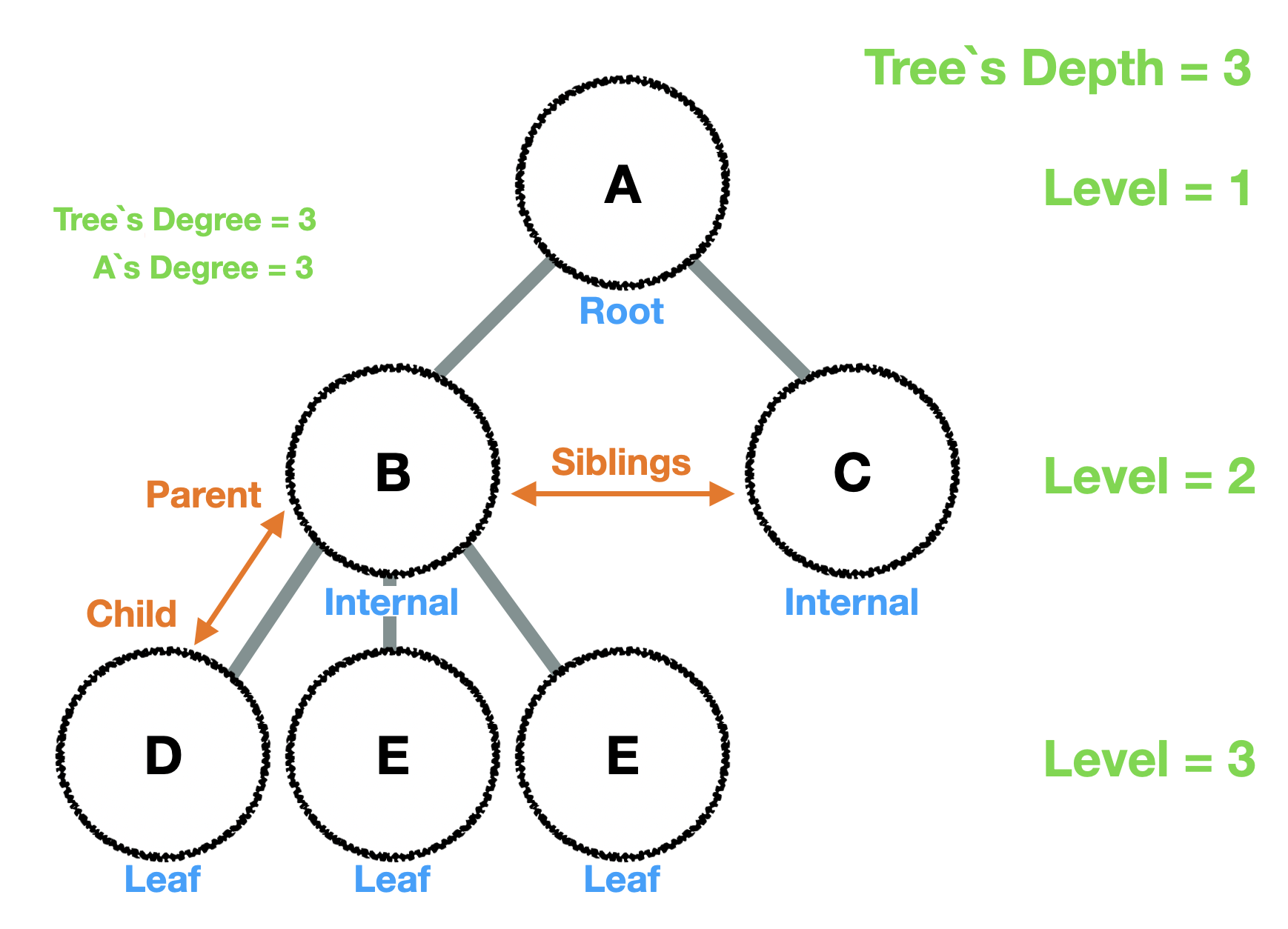
2️⃣ 트리의 용어

트리에서 주로 사용되는 용어들은 다음과 같다.

노드의 차수(degree) : 노드의 부속 트리의 개수
트리의 차수(degree of tree) : 트리의 최대 차수
단말(leaf, terminal) 노드 : 차수가 0인 노드, 즉 맨 끝에 달린 노드
내부(internal, non-terminal) 노드 : 차수가 1 이상인 노드
부모(parent) : 부속 트리(subtree)를 가진 노드
자식(child) : 부모에 속하는 부속노드
형제(sibling) : 부모가 같은 자식 노드들
조상(ancestor) : 노드의 부모 노드들의 총 집합
자손(descendant) : 노드의 부속 트리에 있는 모든 노드들
레벨(level) : 루트 노드들로부터 깊이(루트 노드의 레벨 = 1)
트리의 깊이(depth of tree) : 트리에 속한 노드의 최대 레벨

3️⃣ 트리의 표현 방법

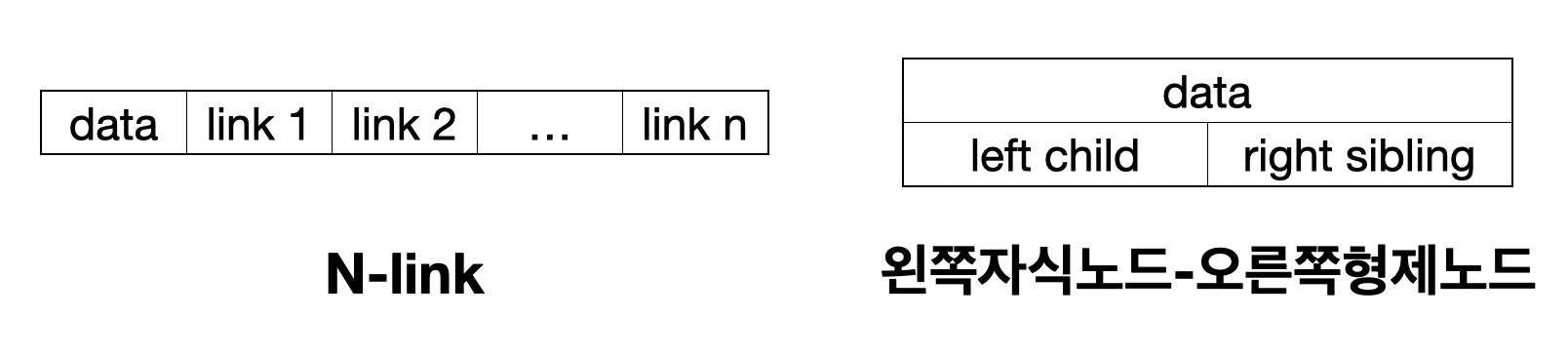
트리를 표현하는 방법은 2가지가 있으며, 왼쪽자식-오른쪽형제 Node 표현법의 경우 일반 트리를 이진 트리로 변환할때에도 사용된다.

n-링크 표현법
각 Node에 자식 수만큼 Link를 저장하는 방식이다.
왼쪽 자식-오른쪽 형제 Node 표현법
Node마다 2개의 링크를 사용하여 첫 번째 자식과 오른쪽 형제를 가리키는 방식이다.

이진 트리(Binary Tree)

이진 트리(Binary Tree)는 일반 트리보다 데이터를 보다 효율적으로 저장할 수 있기 때문에 주로 사용되는 형태이다.

1️⃣ 이진 트리의 정의

자식 Node의 수가 2개 이하인 Tree 구조이며 자식 Node가 비어있을 수도 있다.
2개의 자식 Node는 왼쪽 자식(left child)과 오른쪽 자식(right child)으로 구분된다.

2️⃣ 이진 트리의 성질

이진 트리는 일반 트리와 달리 자식 Node의 수가 제한되어 있기 때문에, 다음과 같은 특징을 가진다.

트리의 Level이 $i$ 일때, 해당 Level에서의 최대 Node 개수는 $2^{i-1}$ 이다.
트리의 Depth가 $h$ 일때, 트리가 가질 수 있는 최대 Node 개수는 $2^{i}-1$ 이다.
트리의 Node가 $n$ 개 일때, 최소 Depth는 $\log_2(n+1)$ 이고 최대 Depth는 $n$ 이다.
$n_0 = n_2 + 1$ ( $n_0$ : 차수가 0인 Node의 수, $n_2$ : 차수가 2인 Node의 수)

또한 아래와 같이 여러 형태의 Binary Tree가 존재한다.

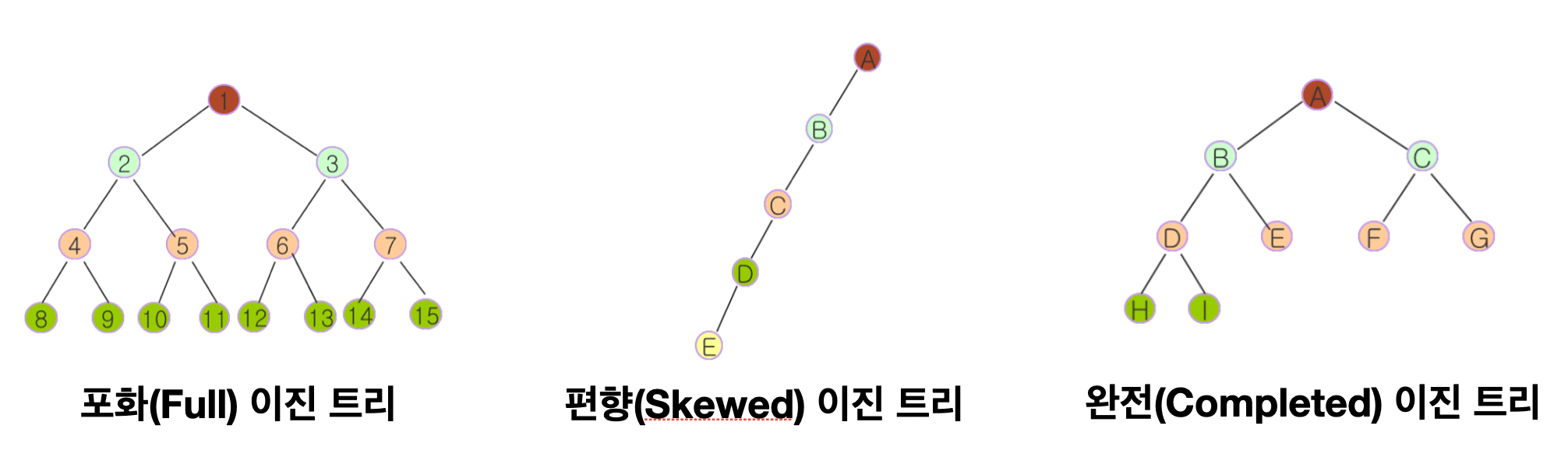
여기서 포화 이진 트리는 모든 Node의 Leaf Node가 꽉 차 있는 상태이고, 완전 이진 트리는 순서대로 Node가 채워져있는 상태를 의미하니 둘 간의 차이에 대해 유의하자.

이진 트리의 구현 및 알고리즘

1️⃣ 이진 트리 구현

이진 트리에서도 이전 선형 자료구조에서와 마찬가지로 정적/동적으로 각각 구현할 수 있다.

이진 트리 정적 구현(배열)

배열을 이용한 정적 구현 방식의 경우, Node를 레벨 순서대로 배열에 저장하는 방식이다.
이때 $i$ 번째 Node의 부모 Node의 위치는 $(i-1)/2$ 또는 0이고 왼쪽 자식 Node는 $2 \cdot i+1$ , 오른쪽 자식 Node는 $2 \cdot i+2$ 에 위치해있다.

다만 이러한 방식은 완전 이진 트리가 아닌 경우 저장 공간의 낭비가 발생한다는 문제점이 있다.

이진 트리 동적 구현(연결리스트)

연결리스트를 이용한 정적 구현 방식의 경우 선형 자료에서와 동일하게 구조체 포인터를 이용하는 방식으로, 배열을 이용한 정적 구현 방식과 달리 저장 공간을 효율적으로 사용할 수 있다는 장점이 있다.
아래와 같이 1개의 data 필드와 2개의 link 필드를 사용하는 방식을 주로 사용하며, 부모에 대한 link를 포함하여 3개 link 필드를 사용하는 방식은 구조의 복잡성 때문에 많이 사용되지 않는다.

2️⃣ 이진 트리 탐색

이진 트리를 탐색하는 방법은 총 4가지가 있다.
Node 레벨의 순서대로 탐색하는 레벨 탐색과 왼쪽/오른쪽 서브트리와 Root Node를 구분하고 이를 정해진 순서대로 탐색하는 전위탐색/중위탐색/후위탐색이 있다. 각각의 탐색 방법에 대한 예시는 아래를 참고하자.

레벨 탐색(Level Traversal)의 경우 Queue 자료구조를 이용한 BFS(Breadth First Search) 방식을 통해 구현할 수 있으며, 전/중/후위 탐색(pre/in/post order Traversal)의 경우 Stack 자료구조 또는 순환 알고리즘을 이용한 DFS(Depth First Search) 방식을 통해 구현할 수 있다.

3️⃣ 이진 트리 알고리즘

이진 트리에서 Node 수 계산, 트리의 깊이 계산, 트리의 복사 및 비교에 대해 어떤식으로 알고리즘을 작성할 수 있는지 아래의 C++ 코드를 통해 살펴보자. 아래의 알고리즘 모두 전체 Node를 탐색하여 원하는 결괏값을 계산한다.

전체 Node 수 계산

전체 Node 수의 경우 각각의 서브트리를 순환 호출하고 1을(현재 Node) 더해주는 방식으로 계산할 수 있다.

int get_node_count(TreeNode *node){
    int count=0;
    if(node != NULL)
        count = 1 + get_node_count(node->left)+get_node_count(node-›right);
    return count;
}

트리 깊이 계산

트리의 깊이도 마찬가지로 각각의 서브트리를 순환 호출하는데, 서브트리에서 구해진 값을 더하는게 아닌 왼쪽/오른쪽 서브트리 중 최댓값만 사용하고 여기에 1을(현재 Node)를 더해주는 방식으로 계산한다.

int get_height(TreeNode *node){
    int height=0;
    if(node != NULL)
        height = 1 + max(get_height(node->left)+get_height(node-›right));
    return height;
}

트리 복사

트리 복사의 경우 전체 트리를 탐색하면서 각각의 Node를 복사하며, 이때 후위 탐색 방식을 이용한다.

tree_ptr copy (tree_ptr original){
    tree_ptr temp;
    if(original){
        temp = (tree_ptr)malloc(sizeof(node));
        temp->left_child = copy(original->left_child);
        temp-›right_child = copy(original->right_child);
        temp->data = original->data;
        return temp;
    }
    return NULL;
}

트리 비교

2개의 이진 트리를 비교하는 것은 동일한 탐색 방식을 진행하며 Node를 만날때마다 비교하면 되는데, 아래는 전위 탐색을 이용한 방식이다.

int equal(tree_ptr first, tree_ptr second){
    return ((!first && !second)
            || (first && second
            && (first->data == second->data)
            && equal(first-> left_child, second->left_child)
            && equal(first->right_child, second->right_child)));
}

이진 트리의 변형

기존의 이진 트리 구조도 효율적이지만, 탐색 시간에 대한 효율성을 더 높이기 위해 새로운 구조 또는 제약 조건을 추가하는 방식을 사용한 변형 이진 트리 구조들이 존재하며 여기에 대해서 알아보자.

1️⃣ 쓰레드 이진 트리

기존의 이진 트리를 탐색할때, Leaf Node에 도착하게 되면 .... (여기서부터 수정)

쓰레드 이진 트리는 일반 이진 트리에서 사용되지 않는 포인터(NULL)를 활용하여, 중위 순회를 보다 효율적으로 수행할 수 있도록 한 구조이다. 자식이 없는 노드의 포인터에 이전 또는 다음 노드 정보를 저장해 탐색 시간을 줄인다.

구현 시, 각 링크가 자식 노드를 가리키는지, 쓰레드인지 구분하는 플래그가 필요하며, 이를 통해 중위 탐색을 반복 없이 쉽게 수행할 수 있다.

2️⃣ 이진 탐색 트리

이진 탐색 트리는 다음과 같은 규칙을 가진 이진 트리이다:

왼쪽 서브트리의 모든 키 < 루트 노드의 키

오른쪽 서브트리의 모든 키 > 루트 노드의 키

이 특성 덕분에 탐색, 삽입, 삭제 시 비교 횟수를 줄일 수 있다. 중위 순회를 하면 노드가 오름차순으로 출력된다.

이진 탐색 트리의 주요 연산:

탐색: 루트부터 비교하며 왼쪽 또는 오른쪽으로 진행

삽입: 탐색 실패 지점에 노드 삽입

삭제: 세 가지 케이스가 있음

단말 노드

하나의 서브트리만 있는 경우

두 개의 서브트리를 가진 경우(가장 유사한 값을 가진 노드로 대체)

이진 탐색 트리의 성능은 트리의 높이에 비례하며, 균형이 잡혀 있으면 log(n)의 시간복잡도로 빠른 탐색이 가능하다. 하지만 한쪽으로 치우친 트리는 성능이 떨어지므로, AVL 트리나 Red-Black 트리와 같은 균형 트리를 사용하는 것이 일반적이다.

Kyeongmin

개발자가 되고 싶은 공장장이🛠

이전 포스트