확률과 통계 #3 Probability Theory

이 글은 최성준 교수님의 확률과 통계 강의를 듣고 정리한 내용입니다.

---

앞서 다뤘던 내용을 먼저 살펴보시면 본 글의 이해에 도움이 됩니다.

• Set Theory (집합론)
• Measure Theory (측도론)

---

먼저 Probability, 확률은 무엇일까?
직전 글에서 Probability는 Normalized Measure 라고 잠깐 언급했었는데,
본 글에서는 Measure를 가지고 Probability가 무엇인지 더 자세히 정의해볼 것이다.

본격적으로 설명하기에 앞서, Probability를 설명할때 흔히 사용하는 육면체 주사위가 있다고 가정해보자.
그럼 아래 그림과 같이 주사위를 통해 나올 수 있는 결과는 1 ~ 6 사이일 것이고,
이러한 결과 공간을 sample space(표본 공간)이라고 말한다.

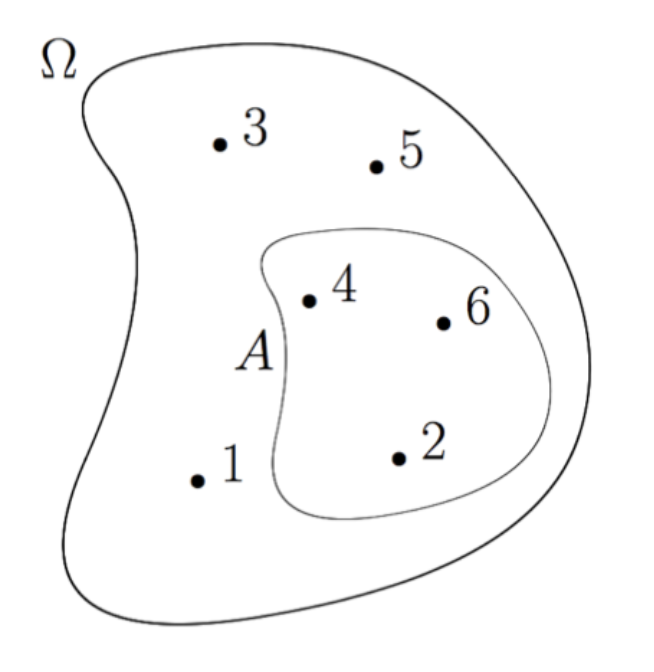
그럼 우리는 sample space $\Omega$ 에 대한 probability measure $P$를 정의할 수 있을 것이고,
이때 Image $P(\text{subset of }\Omega) =$ Probability = sample space의 subset에 해당하는 면적이라고 할 수 있다.

Sample Space

위 내용에서 알 수 있는 것은, probability measure라는 함수가 주어졌을때
발생할 수 있는 모든 결과를 포함한 Universal Set = sample space(표본 공간) 이라는 것이다.

그렇다면 먼저 probability measure가 정의되기 위해서 필요한 sample space에 대해서 좀 더 알아보자.

1️⃣ Sample Space의 조건

어떤 집합 $\Omega = \{s_1, s_2,\;\dots,\;s_n\}$ 이 있을때, 아래 조건을 만족해야 sample space라고 할 수 있다.

1. Mutually Exclusive
   • sample space 내의 결과들은 서로 배타적이어야 한다.
   • 하나의 결과가 발생하면 다른 결과는 발생하지 않아야 한다.
     (ex. 주사위를 던지면 1~6 중 하나의 결과만 나온다.)
2. Collectively Exhaustive
   • sample space 내의 결과들이 모든 결과를 포함해야 한다.
   • 어떤 실험이든 sample space에 속하는 결과가 발생해야 한다.
     (ex. 주사위를 던지면 나올 수 있는 1 ~ 6 이라는 결과는 sample space에 속해야 한다.)
3. Right Granularity
   • sample space는 우리가 관측하고자 하는 대상으로 적절하게 세분화되어야 한다.
   • sample space $\Omega$와 같은 전체 집합이 존재할 때,
     여기에 대한 $\sigma$-field를 $2^{\Omega}, \{\varnothing, \Omega\} \dots$ 등 적절하게 세분화해야 한다.

2️⃣ 용어

위에서 실험, 결과 등과 같은 용어를 사용했었는데 혼동되지 않도록 무슨 의미인지 짚고 넘어가자.

1. outcome (결과)
   : random experiment를 통해 발생할 수 있는 결과이며, 더 이상 나눌 수 없는 결과
2. sample point $\omega$
   : outcome을 의미하는 원소
3. sample space $\Omega$
   : 모든 sample point을 포함하는 집합
4. random experiment (무작위 실험)
   : sample space에서 무작위성을 통해 관측된 outcome

Probability

이전까지 Probability가 정의되기 위한 sample space를 정의해보았으니,
이제 Probability에 대해서 한번 살펴보자.

1️⃣ Probability의 공리

Probability $P$ 는 아래와 같이 $\Omega, \mathscr{A}$로 이루어진 측정 가능한 공간에서 정의되는 함수이며,
※ Measurable Space $(\Omega, \mathscr{A})$의 set function, Probability $P:\;\mathscr{A} \rightarrow [0, 1]$

이러한 Probability $P$ 가 정의되기 위한 공리는 다음과 같다. ($\mathscr{A}$ 는 $\sigma$-field를 의미한다.)

1. $P(\varnothing) = 0$
2. $P(A) \geq 0 \;,\quad \forall A \subset \Omega$
3. $P\left(\bigcup_{i=1}^{k} A_i\right) = \sum_{i=1}^{k} P(A_i) \quad\dots\quad(\text{disjoint set}\;A_i\;\text{and}\;A_j)$
4. $P(\Omega) = 1$

Probability 또한 Measure 이기 때문에 1~3번 조건은 Measure의 조건과 동일하다는 것을 알 수 있고,
Normalized Measure 라고 불리는 것처럼, 4번 조건이 추가되어있는 것을 알 수 있다.

2️⃣ Probability allocation function

그런데 Probability Measure에서의 입력은 subset이다.
subset에는 여러가지 사건(=원소, element)가 포함 될 수 있는데, 각각의 사건에 대한 확률을 어떻게 알 수 있을까?

이걸 위한 방법이 바로 Probability allocation function이다.
우선 Probability allocation function의 입력은 element 이며, Probability Measure와는 다르다.
(당연히 이후에 등장할 Probability mass/density function과도 다르다.)

Probability allocation function은,
Sample Space $\Omega$가 ①이산 / ②연속 인지에 따라 아래와 같이 달라진다.

이산 표본 공간 (Discrete $\Omega$)

아래에서 $p$ (=Probability allocation function), $P$ (=Probability Measure)를 의미하는데,
Probability allocation function의 입력은 element 이다.

연속 표본 공간 (Continuous $\Omega$)

Conditional Probability

그럼 이제 Conditional Probability, 조건부 확률에 대해서 알아보자.
우리가 실생활 측면에서 확률을 활용하려면 단순히 빈도주의 측면에서 생각하는 것보다,
다음과 같은 조건부 확률의 관점에 대해서 생각할 수 있어야 한다.

1️⃣ 정의

먼저 조건부 확률은, 어떠한 사건 $B$가 주어졌을때 사건 $A$가 발생한 확률을 의미한다.
우리가 일상생활에서도 여러 가지 사건들이 존재하고, 어떤 사건이 발생했을때 다른 사건이 일어날 확률과 같이 특정한 조건에서의 확률을 측정하려는 일들이 많을 것인데, 이때 필요한 것이 조건부 확률이다.

앞서 언급한 조건부 확률은 아래의 좌변과 같이 표기하고 이를 우변을 통해 계산하며,
이러한 식이 성립되기 위해서는, $A,B$ 사건 모두 같은 표본 공간 $\Omega$에 존재해야 한다.
($\triangleq$ : 좌변이 우변에 의해 정의됨을 의미)

위 수식을 통해 아래와 같이 유도할 수 있는데 참고만 해두자.

• Chain Rule
  $\begin{aligned} P(A \cap B) &= P(A | B) P(B) \\ P(A \cap B \cap C) &= P(A | B \cap C) P(B \cap C) = P(A | B \cap C) P(B | C) P(C) \end{aligned}$
• Total Probability Law
  $\begin{aligned} P(A) &= P(A \cap B) + P(A \cap B^C) \\ &= P(A | B) P(B) + P(A | B^C) P(B^C) \\ &= \sum_{x \in \{B, B^C\}} P(A | x) P(x) \end{aligned}$

2️⃣ 베이즈 정리

조건부 확률에서 중요한 유도 공식은 베이즈 정리(Bayes` Rule)이다.

기존 조건부 확률 공식을 아래와 같이 유도하는 것을 베이즈 정리라고 하는데,
이는 우리가 알고 있는 사전 지식에 기반하여 우리가 원하는 대상의 확률을 구하거나 또는 추론하는 방식이다.

위의 식에서 각각의 항목을 아래의 용어를 통해 표현하니 참고하자.

• $P(A|B)$, Likelihood (가능도)
• $P(B|A)$, Posterior Probability (사후 확률)
• $P(A)$, Evidence (증거)
• $P(B)$, Prior Probability (사전 확률)

베이즈 정리는 사전 확률(prior probability)의 유무에 따라

Independence

여기서 잠깐 Independence에 대해서 언급하고 넘어가려고 한다.
우리가 확률에서 흔히 말하는 Independent events(독립 사건)이라는 것은 과연 무엇을 의미할까?

사건 $A, B$가 독립 사건이라는 것은 아래 수식을 의미하는데, (P = Probability Measure)
이는 사건 $A, B$의 확률(=subset 면적)이 사건 $A, B$의 교집합의 확률과 동일하다는 것을 말한다.
※ 참고로 $P(A \cap B) = \varnothing$은 직교(Orthogonal)함을 의미한다.

Independence 유형

독립 사건에는 여러 유형이 존재하는데, 그 중 몇가지를 살펴보자.

• pair-wise independence
  : 임의의 2개 사건(subset)을 선택했을 때, 독립 사건인 경우
• 3-wise independence
  : 임의의 3개 사건을 선택했을 때, 독립 사건인 경우 (단, 3-wise $\neq$ pair-wise)
• (mutually) independence
  : 전체 사건 중 임의의 사건들을 선택했을 때, 모두 독립 사건인 경우

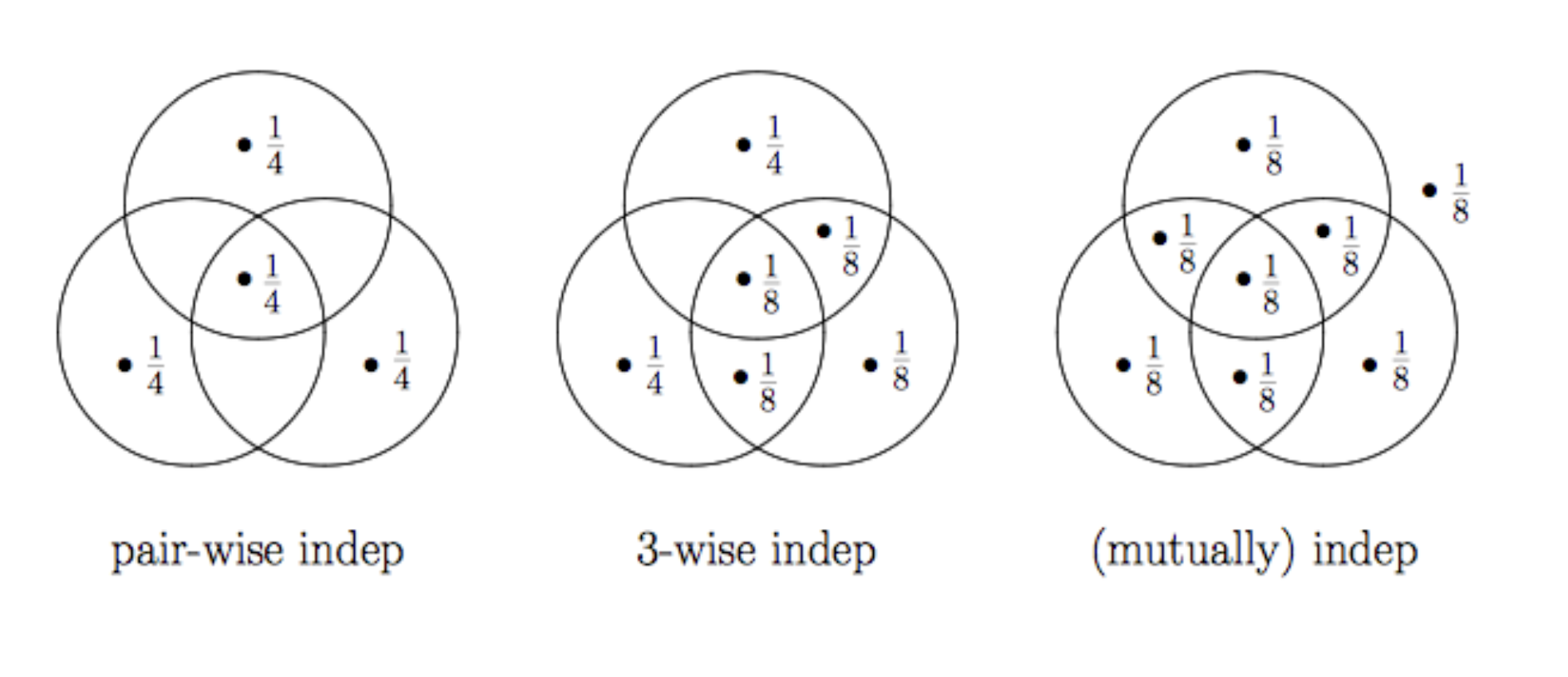
위 그림에서는 mutually independence의 경우, pair/triple wise를 만족하는 경우이나,
사건의 개수가 늘어난다면 모든 사건들의 조합에 대해 독립이어야 한다.