이 글은 최성준 교수님의 확률과 통계 강의를 듣고 정리한 내용입니다.
앞서 다뤘던 내용을 먼저 살펴보시면 본 글의 이해에 도움이 됩니다.
확률 변수
이제 우리가 확률에서 본격적으로 많이 들어봤을만한 확률 변수(Random Variable) 에 대해서 말하려고 한다.
1️⃣ 정의
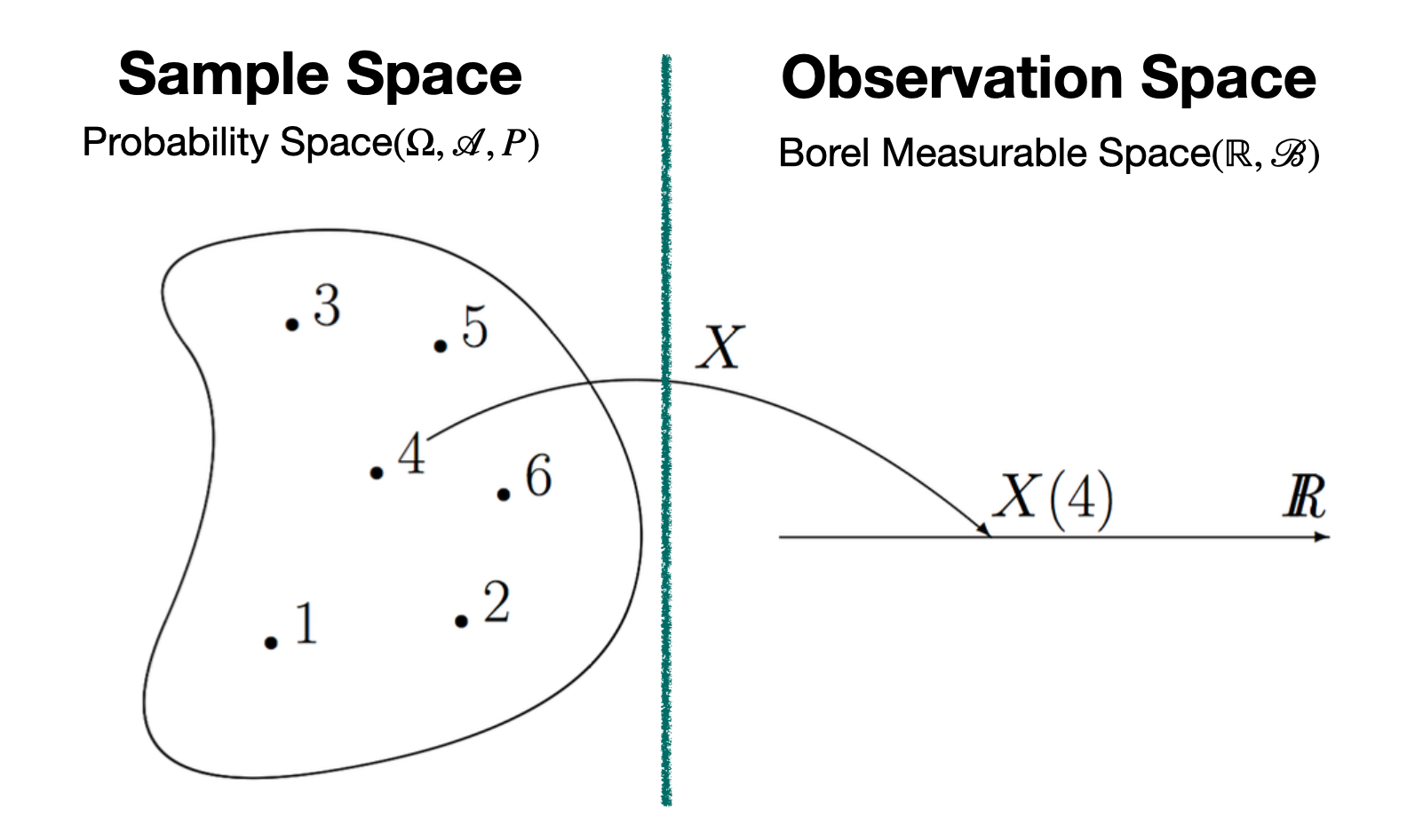
확률 변수 도 Probability Measure와 마찬가지로 입력을 Subset으로 하는 Set Function 이다.확률 변수(아래 그림의 X X X 시키는 함수이다.
이러한 확률 변수를 수식으로 나타내면 아래와 같다.
X : Ω → R such that ∀ B ∈ B , X − 1 ( B ) ∈ A X : \Omega \to \mathbb{R} \text{ such that } \forall B \in \mathscr{B},\;X^{-1}(B) \in \mathscr{A} X : Ω → R such that ∀ B ∈ B , X − 1 ( B ) ∈ A 확률 변수는 연속형 또는 이산형 값을 모두 가질 수 있으며,확률 변수의 값 에 해당되는 B B B 확률 변수값에 대한 확률 이라고 말할 수 있다.
P ( X ∈ B ) ≜ P ( X − 1 ( B ) ) = P ( { ω ∈ Ω : X ( ω ) ∈ B } ) P(X \in B) \triangleq P(X^{-1}(B)) = P(\{ \omega \in \Omega : X(\omega) \in B \}) P ( X ∈ B ) ≜ P ( X − 1 ( B ) ) = P ( { ω ∈ Ω : X ( ω ) ∈ B } )
용어
아래는 확률 변수에 사용되는 용어들인데, 참고만 하자.
Random experiment : 무작위 시행에 대한 결과 (ex. 우리가 실제 주사위를 굴렸을때 나온 값 in Sample Space)Realization : ω ∈ Ω \omega \in \Omega ω ∈ Ω X ( ω ) X(\omega) X ( ω ) Alphabet of X X X X X X Realization Set
2️⃣ 예시
Random Variable을 이용한 확률 계산
Ω = { 1 , 2 , 3 , 4 , 5 , 6 } , A = 2 Ω , X = 1 2 3 4 5 6 10 − 10 20 − 10 30 − 10 \Omega = \{1,2,3,4,5,6\}, \; \mathscr{A}=2^{\Omega},\; X=\begin{array}{|c|c|c|c|c|c|} \hline 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 10 & -10 & 20 & -10 & 30 & -10 \\ \hline \end{array} Ω = { 1 , 2 , 3 , 4 , 5 , 6 } , A = 2 Ω , X = 1 1 0 2 − 1 0 3 2 0 4 − 1 0 5 3 0 6 − 1 0 위와 같이 표본 공간과 확률 변수가 주어졌을때,P ( X ≤ 10 ) = P ( { 1 , 2 , 4 , 6 } = 2 3 P(X \leq 10) = P(\{1, 2, 4, 6\} = \frac{2}{3} P ( X ≤ 1 0 ) = P ( { 1 , 2 , 4 , 6 } = 3 2
Indicator function A A A I A ( ω ) = { 1 , ω ∈ A 0 , else and P ( I A = 1 ) = P ( A ) I_A(\omega) = \begin{cases} 1, & \omega \in A \\ 0, & \text{else} \end{cases} \quad \text{and} \quad P(I_A = 1) = P(A) I A ( ω ) = { 1 , 0 , ω ∈ A else and P ( I A = 1 ) = P ( A )
이산형 확률 변수
위에서 확률 변수는 연속형 / 이산형 값 모두 가질 수 있다고 말했는데,
1️⃣ 이산형 확률 변수
이산형 확률 분포는 아래 수식과 같이 정의할 수 있는데,확률 변수 X X X x i x_i x i x i x_i x i 한다.
{ x i : i = 1 , 2 , … } such that ∑ P ( X = x i ) = 1 \{x_i : i = 1, 2, \dots\} \text{ such that } \sum P(X = x_i) = 1 { x i : i = 1 , 2 , … } such that ∑ P ( X = x i ) = 1 여기서부터는 Sample Space를 비롯해서 Probability Measure, Probability Allocation Function에 대해서는
2️⃣ PMF 정의 및 조건
그렇다면, 기존에 Probability Measure를 통해 측정하던 확률은 어떻게 할 것인가?
이는 Observation Space의 PMF(Probability Mass Function, 확률 질량 함수) 로 정의할 것인데,
아래의 p X ( x ) p_{_X}(x) p X ( x ) P ( X = x ) P(X=x) P ( X = x )
p X ( x ) ≜ P ( X = x ) p_{_X}(x) \triangleq P(X=x) p X ( x ) ≜ P ( X = x ) PMF의 조건
이때 PMF도 마찬가지로 기존의 Probability Measure의 조건을 충족해야 한다.
0 ≤ p X ( x ) ≤ 1 0 \leq p_{_X}(x) \leq 1 0 ≤ p X ( x ) ≤ 1 ∑ x p X ( x ) = 1 \sum_x p_{_X}(x) = 1 ∑ x p X ( x ) = 1 P ( X ∈ B ) = ∑ x ∈ B p X ( x ) P(X \in B) = \sum_{x \in B} p_{_X}(x) P ( X ∈ B ) = ∑ x ∈ B p X ( x )
3️⃣ PMF 예시
3개의 동전이 있을 때, 확률 변수 X X X
그렇다면 PMF는 각각 동전 앞면의 개수에 따라 아래와 같이 정의할 수 있을 것이고,X ≥ 1 X\geq1 X ≥ 1
p X ( x ) = { 1 8 , x = 0 3 8 , x = 1 3 8 , x = 2 1 8 , x = 3 0 , else ⋯ P ( X ≥ 1 ) = 3 8 + 3 8 + 1 8 = 7 8 p_X(x) = \begin{cases} \frac{1}{8}, & x = 0 \\ \frac{3}{8}, & x = 1 \\ \frac{3}{8}, & x = 2 \\ \frac{1}{8}, & x = 3 \\ 0, & \text{else} \end{cases} \quad\quad\quad\cdots\quad\quad P(X \geq 1)=\frac{3}{8} + \frac{3}{8} + \frac{1}{8} = \frac{7}{8} p X ( x ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 8 1 , 8 3 , 8 3 , 8 1 , 0 , x = 0 x = 1 x = 2 x = 3 else ⋯ P ( X ≥ 1 ) = 8 3 + 8 3 + 8 1 = 8 7 이산형 확률 변수의 분포
이산형 확률 변수의 분포는 아래와 같은 유형이 있다.
1️⃣ 베르누이 분포
베르누이 분포(Bernoulli distribution) 는, 하나의 시행에서 두 가지 결과 중 하나(성공 또는 실패)가 나오는 확률분포이다. 아래 PMF에서 p p p 1 − p 1-p 1 − p
확률 질량 함수(PMF)
P ( X = x ) = { p if x = 1 1 − p if x = 0 P(X=x)= \begin{cases} p & \text{if} x=1\\ 1−p & \text{if} x=0\\ \end{cases} P ( X = x ) = { p 1 − p if x = 1 if x = 0 기댓값과 분산
E [ X ] = p Var ( X ) = p ( 1 − p ) \begin{aligned} E[X] &=p \\ \text{Var}(X) &=p(1−p) \end{aligned} E [ X ] Var ( X ) = p = p ( 1 − p ) 2️⃣ 균등 분포
: 균등 분포(Uniform distribution) 는, 모든 값이 동일한 확률을 가지는 확률 분포이다. 균등 분포는 이산 / 연속 확률 변수 둘 다 존재한다.
확률 질량 함수(PMF)
P ( X = x ) = 1 n , x ∈ { x 1 , x 2 , … , x n } P(X=x)= \frac{1}{n}, \quad\quad x\in\{x_1, x_2, \dots, x_n\} P ( X = x ) = n 1 , x ∈ { x 1 , x 2 , … , x n } 기댓값과 분산
E [ X ] = ∑ i = 1 n x i n Var ( X ) = ∑ i = 1 n ( x i − E [ X ] ) 2 n \begin{aligned} E[X] &= \frac{\sum_{i=1}^n x_i}{n} \\ \text{Var}(X) &= \frac{\sum_{i=1}^n (x_i - E[X])^2}{n} \end{aligned} E [ X ] Var ( X ) = n ∑ i = 1 n x i = n ∑ i = 1 n ( x i − E [ X ] ) 2 3️⃣ 기하 분포
: 기하 분포(Geometric distribution) 는, 특정 사건이 처음 발생할 때까지의 시행 횟수를 나타내는 확률분포이며, 각 시행은 독립적이고 성공 확률 p p p
확률 질량 함수(PMF)
P ( X = k ) = ( 1 − p ) k − 1 p , k = 1 , 2 , 3 , … P(X = k) = (1 - p)^{k-1} p, \quad k = 1, 2, 3, \dots P ( X = k ) = ( 1 − p ) k − 1 p , k = 1 , 2 , 3 , … 기댓값과 분산
E [ X ] = 1 p Var ( X ) = 1 − p p 2 \begin{aligned} E[X] &= \frac{1}{p} \\ \text{Var}(X) &= \frac{1 - p}{p^2} \end{aligned} E [ X ] Var ( X ) = p 1 = p 2 1 − p 4️⃣ 이항 분포
: 이항 분포(Binomial Distribution) 는, 고정된 시행 횟수 n n n p p p
확률 질량 함수(PMF)
P ( X = x ) = ( n k ) p k ( 1 − p ) n − k , k = 0 , 1 , 2 , … , n P(X=x)= \binom{n}{k} p^k (1-p)^{n-k}, \quad k = 0, 1, 2, \dots, n P ( X = x ) = ( k n ) p k ( 1 − p ) n − k , k = 0 , 1 , 2 , … , n 기댓값과 분산
E [ X ] = n ⋅ p Var ( X ) = n ⋅ p ⋅ ( 1 − p ) \begin{aligned} E[X] &= n \cdot p \\ \text{Var}(X) &= n \cdot p \cdot (1-p) \end{aligned} E [ X ] Var ( X ) = n ⋅ p = n ⋅ p ⋅ ( 1 − p ) 5️⃣ 음이항 분포
: 음이항 분포(Negative Binomial Distribution) 는, k k k r r r
확률 질량 함수(PMF)
P ( X = x ) = ( k + r − 1 k ) ( 1 − p ) r p k P(X=x)= \binom{k+r-1}{k} (1-p)^{r}p^k P ( X = x ) = ( k k + r − 1 ) ( 1 − p ) r p k 기댓값과 분산
E [ X ] = r p Var ( X ) = r ( 1 − p ) p 2 \begin{aligned} E[X] &= \frac{r}{p} \\ \text{Var}(X) &= \frac{r(1-p)}{p^2} \end{aligned} E [ X ] Var ( X ) = p r = p 2 r ( 1 − p ) 6️⃣ 포아송 분포
: 포아송 분포(Poisson Distribution) 는, 단위 시간 또는 공간에서 특정 사건이 발생하는 횟수를 나타내며, 사건 발생은 독립적이며 고정된 비율 λ \lambda λ
확률 질량 함수(PMF)
P ( X = x ) = λ k e − λ k ! , k = 0 , 1 , 2 , … P(X=x)= \frac{\lambda^k e^{-\lambda}}{k!}, \quad k = 0, 1, 2, \dots P ( X = x ) = k ! λ k e − λ , k = 0 , 1 , 2 , … 기댓값과 분산
E [ X ] = λ Var ( X ) = λ \begin{aligned} E[X] &= \lambda \\ \text{Var}(X) &= \lambda \end{aligned} E [ X ] Var ( X ) = λ = λ 연속형 확률 변수
1️⃣ 연속형 확률 변수
연속형 확률 분포는 아래 수식과 같이 정의할 수 있는데,확률 변수 X X X x i x_i x i x i x_i x i 한다.
f X ( x ) such that P ( X ∈ B ) ∫ B f X ( x ) d x f_X(x) \text{ such that } P(X\in B) \int_B f_X(x)dx f X ( x ) such that P ( X ∈ B ) ∫ B f X ( x ) d x 2️⃣ PDF 정의 및 조건
이는 Observation Space의 PDF(Probability Density Function, 확률 질량 함수) 로 정의할 것인데,
아래의 f X ( x ) f_{_X}(x) f X ( x ) P ( X = x ) P(X=x) P ( X = x )
f X ( x ) ≜ P ( X = x ) f_{_X}(x) \triangleq P(X=x) f X ( x ) ≜ P ( X = x ) 이때 PDF도 마찬가지로 기존의 Probability Measure의 조건을 충족해야 한다.
∫ − ∞ ∞ f X ( x ) d x = 1 … ( 1 < f X ( x ) is possible ) \int^\infty_{-\infty} f_X(x)dx = 1 \quad\dots\quad (1 < f_X({x}) \text{ is possible}) ∫ − ∞ ∞ f X ( x ) d x = 1 … ( 1 < f X ( x ) is possible ) P ( X ∈ B ) = ∫ x ∈ B f X ( x ) d x P(X \in B) = \int_{x\in B} f_X(x) dx P ( X ∈ B ) = ∫ x ∈ B f X ( x ) d x
연속형 확률 변수의 분포
연속형 확률 변수의 분포는 아래와 같은 유형이 있다.
1️⃣ 균등 분포
균등 분포(Uniform distribution) 는, 특정 구간 [ a , b ] [a,b] [ a , b ]
확률 밀도 함수(PDF)
f ( x ) = { 1 b − a , if a ≤ x ≤ b 0 , otherwise f(x) = \begin{cases} \frac{1}{b-a}, & \text{if } a \leq x \leq b \\ 0, & \text{otherwise} \end{cases} f ( x ) = { b − a 1 , 0 , if a ≤ x ≤ b otherwise 기댓값과 분산
E [ X ] = a + b 2 Var ( X ) = ( b − a ) 2 12 \begin{aligned} E[X] &= \frac{a + b}{2} \\ \text{Var}(X) &= \frac{(b-a)^2}{12} \end{aligned} E [ X ] Var ( X ) = 2 a + b = 1 2 ( b − a ) 2 2️⃣ 지수 분포
지수 분포(Exponential distribution) 는, 사건이 발생하는 시간 간격을 모델링한다. 사건이 포아송 프로세스(Poisson Process)를 따를 때, 연속적 시간 간격은 지수 분포를 따른다.
확률 밀도 함수(PDF)
f ( x ) = { λ e − λ x , x ≥ 0 0 , otherwise f(x) = \begin{cases} \lambda e^{-\lambda x}, & x \geq 0 \\ 0, & \text{otherwise} \end{cases} f ( x ) = { λ e − λ x , 0 , x ≥ 0 otherwise 기댓값과 분산
E [ X ] = 1 λ Var ( X ) = 1 λ 2 \begin{aligned} E[X] &= \frac{1}{\lambda} \\ \text{Var}(X) &= \frac{1}{\lambda^2} \end{aligned} E [ X ] Var ( X ) = λ 1 = λ 2 1 3️⃣ 라플라스 분포
라플라스 분포(Laplace distribution) 는, 평균 주변에서의 변화가 기하급수적으로 감소하는 대칭적인 분포로 정규 분포와 유사하다. 이는 데이터의 변화가 급격한 경우를 모델링하는 데 적합하다.
확률 밀도 함수(PDF)
f ( x ) = 1 2 b exp ( − ∣ x − μ ∣ b ) f(x) = \frac{1}{2b} \text{exp}\Big({-\frac{|x-\mu|}{b}}\Big) f ( x ) = 2 b 1 exp ( − b ∣ x − μ ∣ ) 기댓값과 분산
E [ X ] = μ Var ( X ) = 2 b 2 \begin{aligned} E[X] &= \mu \\ \text{Var}(X) &= 2b^2 \end{aligned} E [ X ] Var ( X ) = μ = 2 b 2 4️⃣ 가우시안 분포
가우시안 분포(Gaussian distribution) 또는 정규 분포라고 말하며 이는, 평균과 분산만으로 정의가 가능한 분포로 가장 많은 확률 변수의 분포로 사용되는 분포이다.
확률 밀도 함수(PDF)
f ( x ) = 1 2 π σ 2 exp ( − 1 2 ( x − μ σ ) 2 ) f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \text{exp}\Big({-\frac{1}{2}\big(\frac{x-\mu}{\sigma}}\big)^2\Big) f ( x ) = 2 π σ 2 1 exp ( − 2 1 ( σ x − μ ) 2 ) 기댓값과 분산
E [ X ] = μ Var ( X ) = σ 2 \begin{aligned} E[X] &= \mu \\ \text{Var}(X) &= \sigma^2 \end{aligned} E [ X ] Var ( X ) = μ = σ 2 5️⃣ 코시 분포
코시 분포(Cauchy distribution) 는, 평균과 분산이 정의되지 않는 분포이며, 분포의 꼬리가 두꺼운 형태로 이상치가 많을 때 주로 사용된다.
확률 밀도 함수(PDF)
f ( x ) = 1 π γ ( 1 + ( x − x 0 γ ) 2 ) f(x) = \frac{1}{\pi \gamma \Big( 1 + \left(\frac{x-x_0}{\gamma}\right)^2 \Big)} f ( x ) = π γ ( 1 + ( γ x − x 0 ) 2 ) 1 Moment
Moment 는 Random Variable의 분포 형태(중심, 퍼짐, 비대칭성 등)와 같이 다양한 특성을 설명하기 위해 사용되며, 일반적으로 n n n E [ X n ] E[X^n] E [ X n ]
Moment 종류 수식 정의 1st Moment m X = E [ X ] m_{_X} = E[X] m X = E [ X ] 평균 : 데이터의 중심 위치를 나타냄2nd Moment σ X 2 = Var ( X ) = E [ ( X − m X ) 2 ] \sigma_X^2 = \text{Var}(X) = E[(X - m_{_X})^2] σ X 2 = Var ( X ) = E [ ( X − m X ) 2 ] 분산 : 평균 주변 데이터의 퍼짐 정도3rd Moment E [ ( X − m X ) 3 ] σ X 3 \frac{E[(X - m_{_X})^3]}{\sigma_X^3} σ X 3 E [ ( X − m X ) 3 ] 비대칭성 (Skewness): 꼬리 방향과 정도4th Moment E [ ( X − m X ) 4 ] σ X 4 \frac{E[(X - m_{_X})^4]}{\sigma_X^4} σ X 4 E [ ( X − m X ) 4 ] 첨도 (Kurtosis): 꼬리 두께와 중심 집중도
Joint Moment
Joint Moment 는, 2개 이상의 Random Variable 간의 관계를 설명하는데 사용되며, 아래와 같은 종류가 있다.
Moment 종류 수식 정의 correlation E [ X Y ] E[XY] E [ X Y ] 상관관계, 두 변수 간의 선형 관계의 강도와 방향 covariance E [ ( X − m X ) ( Y − m Y ) ] E[(X-m_{_X})(Y-m_{_Y})] E [ ( X − m X ) ( Y − m Y ) ] 공분산 cov ( X , Y ) \text{cov}(X, Y) cov ( X , Y ) correlation coefficient cov ( X , Y ) σ X σ Y \frac{\text{cov}(X, Y)}{\sigma_X\sigma_Y} σ X σ Y cov ( X , Y ) 상관계수 ρ X Y \rho_{_{XY}} ρ X Y
그리고 Random Variable 간의 관계에 따라 아래의 식이 성립한다.
uncorrelated 인 경우, E [ X Y ] = E [ X ] E [ Y ] E[XY] = E[X]E[Y] E [ X Y ] = E [ X ] E [ Y ] independent ⇒ \Rightarrow ⇒ uncorrelated 이지만, 그 반대는 성립하지 않는다.orthogonal 인 경우, E [ X Y ] = 0 E[XY] = 0 E [ X Y ] = 0