이진트리 시간복잡도

이진 트리

다양한 분야에서 많이 사용되고 있는 자료구조인 트리 중에서 이진트리에 대해 작성하고자 한다.

먼저 트리는 나무를 뒤집어 놓은 모양과 비슷하다고 트리라고 이름이 붙여졌다고 한다..

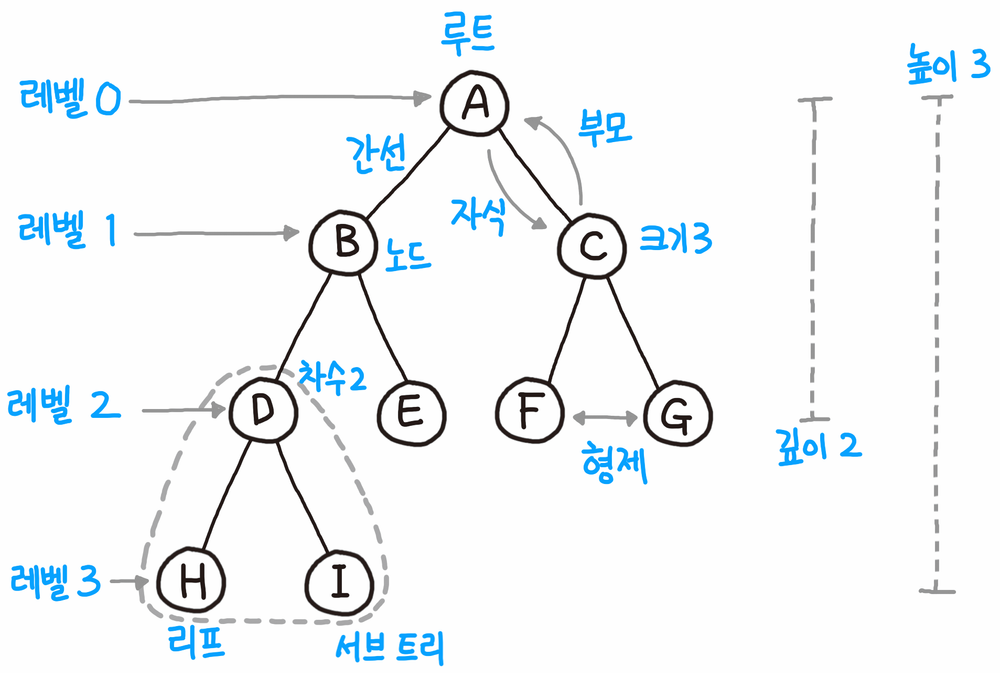
이 그림처럼 모든 동그라미를 노드, 노드와 노드를 이어주는 선을 간선이라고 합니다.

트리의 높이(h)는 루트 노드에서 말단 노드까지의 가장 긴 경로의 간선 수입니다. 트리의 특정 깊이를 가지는 노드의 집합을 레벨(level)이라고 합니다.

그럼 이진트리란 무엇일까요?

말 그대로 모든 노드의 자식노드가 최대 2개의 노드만을 가진 트리를 이진트리라고 합니다.

정 이진트리는 모든 노드의 자식노드가 2개로 꽉 채워진 트리를 말합니다.

탐색

이진트리의 원소를 탐색 하는데 많이 사용합니다.

이때 시간 복잡도는 O(logn)입니다.

어떻게 이렇게 나왔는지 알아봅시다.

빅오 표기법은 최대값을 기준으로 표기하기 때문에, 제일 말단 노드에 원하는 값이 있을경우 높이(h)만큼의 노드를 탐색해야합니다.

그럼 시간복잡도는 O(h)이지만 데이터의 수로 표기하는게 정석이기 때문에 이를 h를 n에 관한 식으로 바꿔서 표기해줘야합니다.

따라서

이는 위에 그림처럼 루트 노드를 depth 0으로 지정한 경우 이와 같은 공식에 따라

하지만 사람마다 케바케로 루트 노드를 depth 1로 지정하여 사용하는 경우가 있다. 이 경우에는 아래와 같은 방식으로 시간 복잡도를 계산하면 된다.

이와 같은 방식으로 계산되어 시간복잡도는

따라서 어떻게 depth를 결정하던간에 시간 복잡도는

이 된다.