NURBS 란
NURBS 는 Non-uniform rational basis spline 의 약자로, 일반적으로 컴퓨터 그래픽스에서 곡선이나 표면을 표현할 때 많이 사용한다. NURBS 이외에도 Spline 을 표현하는 방법으로 B-Spline 이나 Bezier Spline 등이 있으나, NURBS 를 활용하였을 때, 다른 Spline 표현 방법으로 표현할 수 있는 모든 Spline 을 표현할 수 있기 때문에 일반적으로 많이 사용되고 있다.
이 글에서는 NURBS 를 이용해 Spline 이 표현되어 있을 때, Spline 을 해석하는 방법을 다룰것이다.
Expressions
먼저 NURBS 를 표현할 때 사용하는 용어를 먼저 확인해보자.
Order
Order 는 차수 라고도 표현하는데, 스플라인을 그릴 때 얼마나 많은 제어점의 영향을 받을 것인지 결정하는 값이다. 일반적으로 1, 2, 3, 5차가 사용되고, NURBS 로 그려진 원은 2차, 그외 자유형상은 3차 또는 5차로 표현된다. 이렇게 설명해도 직관적으로 와닿지는 않으니 아래의 이미지를 확인해보자.
우선 1차 NURBS 이다.
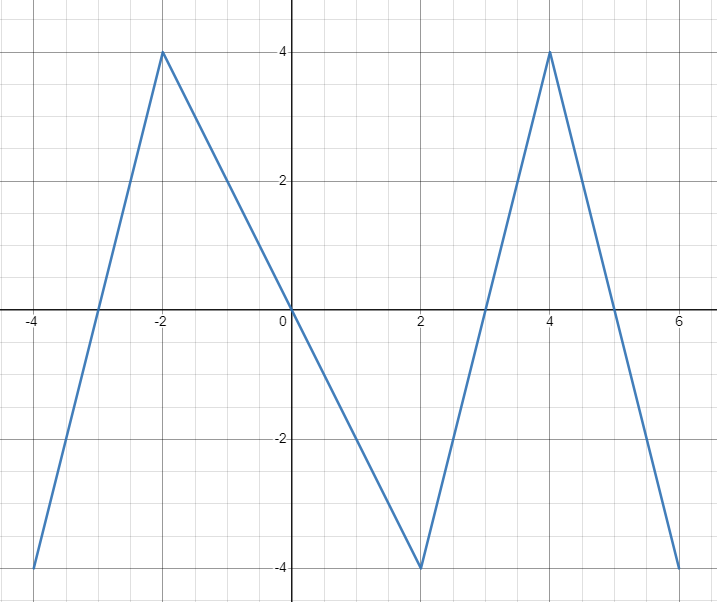
딱 보면 보이는것처럼 이건 곡선보다는 폴리곤에 가깝다. Spline 을 그릴 때 한점의 영향만 받으니 아무래도 값이 이렇게 표현된다.
다음은 2차 NURBS 이다.
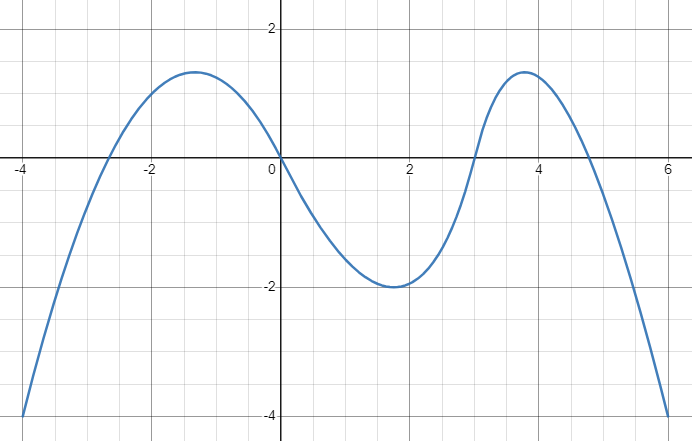
이제 곡선 부분이 보이기 시작한다.
다음은 3차 NURBS 이다.
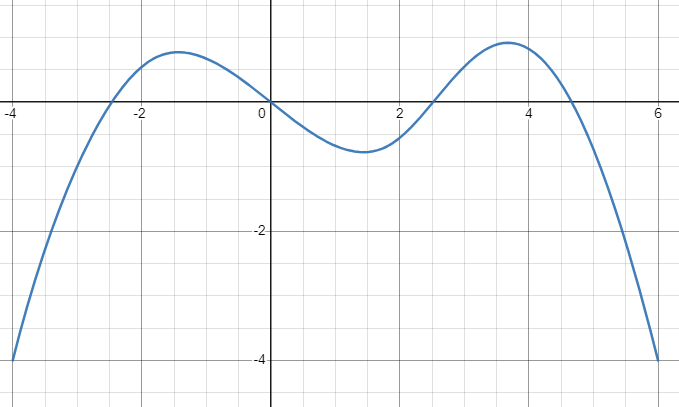
단순하게 생각하면 차수가 높을수록 더 많은 점의 영향을 받아 Spline 을 그리게 되고, 따라서 낮은 차수에 비해 복잡한 곡선의 표현이 가능하다고 생각하면 될 것 같다.
Control Point
Control Point 는 곡선을 결정할 때 기준으로 할 점이다. 아래의 그래프를 확인해보자.
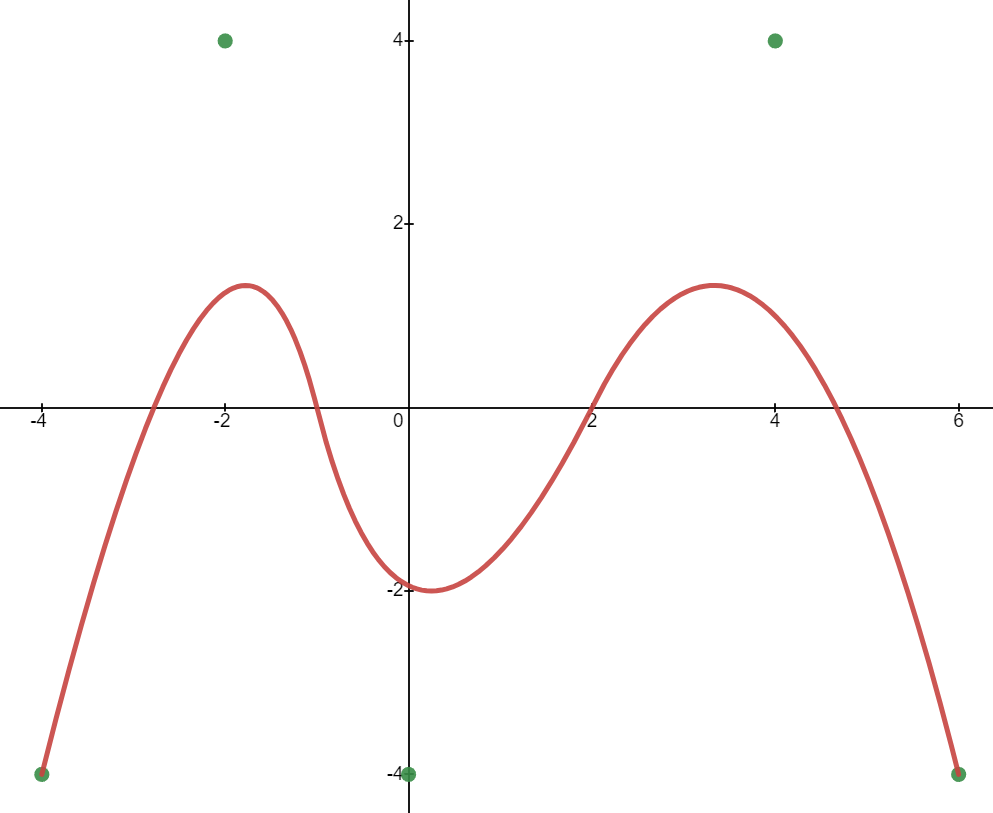
이 그래프는 NURBS 를 이용해 그린 2차원 Spline인데, 빨간 선이 생성된 NURBS 곡선이고, 초록색 점이 Control Point 이다. NURBS 곡선은 위치에 따라 이 초록색 점들 중 특정 점의 위치를 어떤 비율로 더할것인가를 기준으로 경로를 생성한다.
기본적인 제약 조건은 아래와 같다.
- Control Point 의 개수는 0이 될 수 없다.
- Control Point 의 개수는 Order + 1 과 같거나 이보다 많아야 한다.
Knot
Knot 는 NURBS 의 특정 지점이 어떤 Control Point 의 영향을 받을건지 결정하는 스칼라 값이다. 조금 내용이 어려워 보이는데, 이해하고 나면 전혀 어렵지 않다.
먼저 샘플로 Control Point 에서도 사용했었던 이미지를 가져와서 확인해보자.

Sample Values
이 2차 NURBS 커브는 아래의 값을 이용해 정의하였다.
Size of Knot set
는 Control Point 집합이고, 는 Knot 값의 집합이다.
Knot 의 값은 Control Point 의 개수와 NURBS 의 차수에 따라 결정된다.
공식은 아래와 같다.
여기에서 은 NURBS 의 차수이다.
이 공식을 확인하고 위의 값을 확인해보면 Control Point 는 5개이고, 2차 NURBS 이기 때문에 Knot 는 8개이다.
Describe Knot value
Knot 값이 어떻게 영향을 미치는지 알려면 먼저 간단하게 NURBS 의 차수에 따라 영향을 받는 포인트가 결정된다는 것을 이해해야 한다.
예를들어 n차 NURBS 커브가 있다 생각하고, 이 곡선의 시작점을 0, 끝점을 k로 한 상태에서 그 사이의 한 지점을 u 라고 하자. 이 경우 u의 위치를 연산하기 위해서는 해당 NURBS 가 몇차 NURBS 인지에 따라 영향을 받는 Control Point 의 개수가 결정된다.
- 1차 NURBS : 1 ~ 2개의 점
- 2차 NURBS : 1 ~ 3개의 점
- 3차 NURBS : 1 ~ 4개의 점
- 5차 NURBS : 1 ~ 6개의 점
이유는 아래의 공식을 보면 알수 있지만, 일단 지금은 Knot 를 이해하는 것이기 때문에 먼저 이까지만 알고 있자. 이렇게 보면 1 ~ 개의 점에게 영향을 받을 수 있다는 것을 알수있다. 그런데 정확하게 몇개의 점에 영향을 받는지는 알기 어렵다.
따라서 존재하는 값이 Knot 값이다.
위의 Knot 값을 다시 가져와보자.
값을 보면 알겠지만 처음 값은 0 이고, 끝값은 3 이다. 위의 내용에 따라 u 는 0 ~ 3 사이의 실수값이 된다. 설명을 위해 은 로, 는 정도로 값을 설정해보자.
우선 첫번째 점이 지정된 값에 영향을 주는지 확인해 볼 것이다.
의 첫번째 값을 기준으로 개의 값을 가져와보면 의 값이 된다.
여기에서 가장 큰 값과 작은 값을 가져오면 각각 , 이다.
그런다음 이 두 값 사이에 값이 있는지 확인해 보면 된다.
지금은 의 공식이 되는데, 이니까 이 식은 부정이 된다.
따라서 첫번째 점은 영향을 받지 않는다는 것을 알 수 있다.
이와 같은 방법으로 두번째 값에 대해 같은 과정을 수행하면 마찬가지로 값이 부정이 되지만, 3번째 값에 대해 같은 과정을 수행하면 로 값이 참이 된다. 위와 같이 모든 점에 대해서 이 처리 과정을 수행하면 3, 4번째 값을 기준으로 작업을 수행할 때 참이 됨을 알 수 있고, 지점은 3, 4번째 Control Point 값의 비율 조합으로 계산된다는 것을 알 수 있다.
Knots set rules
위의 설명을 통해 알 수 있다시피 값은 오른쪽으로 갈때 마다 값이 같거나 커져야 한다는 것을 알수있다. 이 외에도 몇가지 규칙이 있는데 이걸 다 설명하려면 포스트가 너무 길어지기 때문에 일단은 전체적인 규칙과 성질을 확인하고 넘어가자.
- Knot 값의 개수는 이여야 한다.
- Knot 값은 이전 값과 같거나 커야 한다.
- Knot 값은 회보다 많이 반복될 수 없다.
ex) 2차 NURBS 에서 는 허용되지 않는다. - Knot 값을 상수배 하였을 때의 Spline과 상수배 하기 이전의 Spline 은 같다.
Weights
Weight 는 Knot 값을 통해 특정 지점에서의 위치를 연산할 때, 특정한 Control Point 에서 받는 영향을 조정하기 위해서 사용한다. 예를들어 특정 지점에서 1, 2, 3 번 Control Point 의 영향을 받는다 하면, Weight 값의 비율에 따라 특정 Control Point 의 영향을 더 많이 받거나 적게 받을 수 있다.
다시 조금전의 그림을 가져와보자.

이 그림에서는 모든 점의 Weight 값이 1로 고정되어 있는데, 여기에서 3번 지점의 Weight 값을 0.5로 조정하면, 3번 지점의 영향을 적게 받아 아래와 같이 그래프의 모양이 변하게 된다.
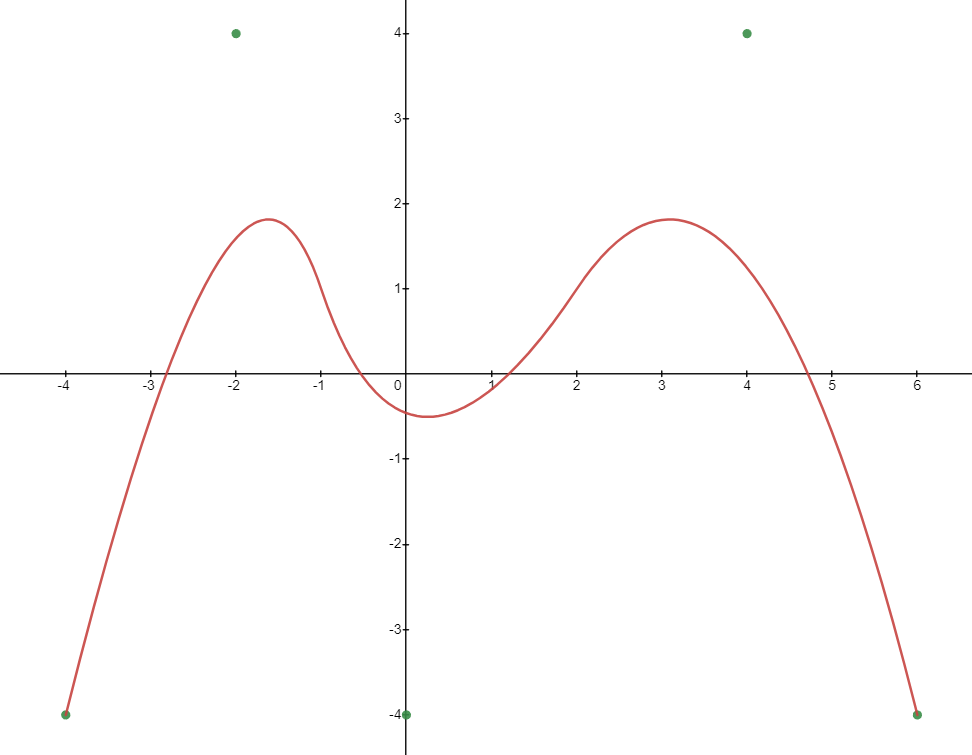
딱 보면 알겠지만, 가운데 움푹 패인 부분이 기존에는 -2에 가깝게 내려갔는데, 지금은 -1에도 한참 못미친것을 확인할 수 있다.
Fomula
NURBS 에서 사용하는 용어와 각각에 대한 설명이 끝났으니 이제 공식을 확인해보자.
먼저 사용될 상수 값은 아래와 같다.
- : Control Point 집합
- : Control Point 의 개수
- : Knots 값 집합
- : Weight 값 집합
- : NURBS 의 차수
- : 연산할 곡선의 지점 ()
NURBS 에서 지점에서 번째 Control Point 의 영향력을 결정하는 공식으로 아래의 공식을 사용한다.
단 이 0일때에는 아래의 조건에 따라 값을 결정한다.
여기에서 사용되는 와 는 일종의 activation 함수로 생각하면 된다. 공식은 아래와 같다.
마지막으로 아래의 공식을 통해 NURBS 커브를 결정하게 된다.
이 공식에서 영향력을 결정하는 부분을 별도의 함수로 빼면 아래와 같이 정리할 수 있다.
Implementation
위에서 본 공식을 Python 을 통해 구현하고, matplotlib 을 이용해 시각화해보자.
개발은 Python 3.8.3 환경의 jupyter notebook 에서 진행하였다.
Full code
import numpy
import matplotlib.pyplot as plt
class Nurbs:
degree = 0
control_points = []
knots = []
weights = []
def __init__(self, degree, control_points, knots, weights):
self.degree = degree
self.control_points = control_points
self.knots = knots
self.weights = weights
if len(self.control_points) < self.degree + 1:
raise Exception("Too few control_points provieded")
if len(self.control_points) != len(self.weights):
raise Exception("Weight array size mismatch with control_points size")
if degree + len(self.control_points) + 1 != len(self.knots):
raise Exception("Knots size mismatch with expected size.")
def get_point(self, u):
point = numpy.zeros((2))
accum_effective = 0.0
for i in range(0, len(self.control_points)):
effective = self.calc_effective(i, self.degree, u) * self.weights[i]
accum_effective = accum_effective + effective
point = point + numpy.array(self.control_points[i]) * effective
point = point / accum_effective
return point
def calc_effective(self, i, n, u) -> float:
if n == 0:
return 1 if self.knots[i] <= u and u <= self.knots[i + 1] else 0
f = self.__bias_function(i, n, u)
g = 1 - self.__bias_function(i + 1, n, u)
effective = (f * self.calc_effective(i, n - 1, u) + g * self.calc_effective(i + 1, n - 1, u))
return effective
def __bias_function(self, i, n, u):
return (u - self.knots[i]) / (self.knots[i + n] - self.knots[i]) if ((self.knots[i + n] - self.knots[i])) != 0 else 0
degree = 2
control_points = [
[-4.0, -4.0],
[-2.0, 4.0],
[ 0.0, -4.0],
[ 4.0, 4.0],
[ 6.0, -4.0]
]
knots = [0, 0, 0, 1, 2, 3, 3, 3]
weights = [1, 1, 1, 1, 1]
curve = Nurbs(degree, control_points, knots, weights)
points = numpy.array([curve.get_point(i) for i in numpy.linspace(0, 3, 100)])
plt.scatter(points[0:,0], points[0:,1])
plt.xlim(-4,6)
plt.ylim(-4,4)
plt.show()Import libraries
먼저 NURBS 를 연산할 때 사용할 numpy 라이브러리와 시각화 할 때 사용할 matplotlib 을 import 해 주어야 한다.
import numpy
import matplotlib.pyplot as pltNURBS constructor
이제 NURBS 연산을 위한 클래스를 정의할건데, 데이터의 유효성을 검증하기 위한 생성자를 먼저 만들어보자.
class Nurbs:
degree = 0
control_points = []
knots = []
weights = []
def __init__(self, degree, control_points, knots, weights):
self.degree = degree
self.control_points = control_points
self.knots = knots
self.weights = weights
if len(self.control_points) < self.degree + 1:
raise Exception("Too few control_points provieded")
if len(self.control_points) != len(self.weights):
raise Exception("Weight array size mismatch with control_points size")
if degree + len(self.control_points) + 1 != len(self.knots):
raise Exception("Knots size mismatch with expected size.")위에서 여러가지 조건이 있었는데, 이 코드에서는 값의 유효성은 검사하지 않고, 데이터의 개수만을 체크하였다. 생성자에서 차수, Control Points, Knots, Weight 값을 받고, 클래스의 멤버 변수로 값을 저장한다.
Effective function
이번에는 위의 공식에서 로 설명된 Control Point 의 영향력을 결정하는 함수를 구현해보자.
class Nurbs:
def calc_effective(self, i, n, u) -> float:
if n == 0:
return 1 if self.knots[i] <= u and u <= self.knots[i + 1] else 0
f = self.__bias_function(i, n, u)
g = 1 - self.__bias_function(i + 1, n, u)
effective = (f * self.calc_effective(i, n - 1, u) + g * self.calc_effective(i + 1, n - 1, u))
return effective
def __bias_function(self, i, n, u):
return (u - self.knots[i]) / (self.knots[i + n] - self.knots[i]) if ((self.knots[i + n] - self.knots[i])) != 0 else 0위의 공식을 그대로 코드로 옮긴 것이기 때문에 크게 설명해야 할 부분은 없을 것이라 생각한다.
Get NURBS point
다음으로 NURBS 포인트를 결정하는 에 해당하는 함수를 작성해보자.
class Nurbs:
def get_point(self, u):
point = numpy.zeros((2))
accum_effective = 0.0
for i in range(0, len(self.control_points)):
effective = self.calc_effective(i, self.degree, u) * self.weights[i]
accum_effective = accum_effective + effective
point = point + numpy.array(self.control_points[i]) * effective
point = point / accum_effective
return point이 함수는 아래의 공식을 참고하여 구현하였다.
먼저 self.calc_effective 함수를 호출해 위 식의 에 해당하는 값을 구한다. 그리고 구한 값에 에 해당하는 self.weights 배열에서 값을 가져와 가중치를 적용해 준다.
이렇게 구해진 값은 accum_effective 변수에 적산해 분모에 해당하는 값을 연산하면서, 이 값과 Control Point 인 에 해당하는 self.control_points 에서 해당하는 값을 가져와 point 변수에 위치 값을 적산한다.
이 과정을 모든 Control Point 에 대하여 수행하면 최종적으로 point 변수에 분자에 해당하는 값이 계산되고, accum_effective 변수에 분모에 해당하는 값이 연산되기 때문에, 이 두 값을 나누어 최종적인 위치 값을 얻을 수 있게 된다.
Test with sample parameters
만들어진 NURBS 가 정상적으로 동작하는지 테스트해보자. 테스트할 때 사용할 파라미터는 아래와 같다.
- 차수 : 2
- Control Points :
- Knots :
- Weights :
위의 값을 이용해 Spline 을 그리면 아래의 이미지와 같은 곡선을 얻을 수 있다.

원하는 결과값을 확인하였으니 이제 python 코드가 정상적으로 동작하는지 확인해보자.
degree = 2
control_points = [
[-4.0, -4.0],
[-2.0, 4.0],
[ 0.0, -4.0],
[ 4.0, 4.0],
[ 6.0, -4.0]
]
knots = [0, 0, 0, 1, 2, 3, 3, 3]
weights = [1, 1, 1, 1, 1]
curve = Nurbs(degree, control_points, knots, weights)
points = numpy.array([curve.get_point(i) for i in numpy.linspace(0, 3, 1000)])
plt.scatter(points[0:,0], points[0:,1])
plt.xlim(-4,6)
plt.ylim(-4,4)
plt.show()먼저 degree, control_points, knots, weights 변수를 선언하고, 조금전에 확인한 값을 대입한다. 그리고 이 값들을 이용해 Nurbs 객체를 생성해 curve 변수에 저장한다.
그리고 points 배열을 만들어 여기에 얻어진 점들을 쭉 넣는데, numpy.linspace 함수를 이용해 knots 의 시작값인 0 부터 3 까지의 값을 1000 등분 하여 각각의 값으로 curve.get_point 함수를 실행하고 실행 결과를 배열로 만든다.
이후 matplotlib 을 이용해 데이터를 출력하면 아래의 이미지와 같이 데이터가 출력된다.
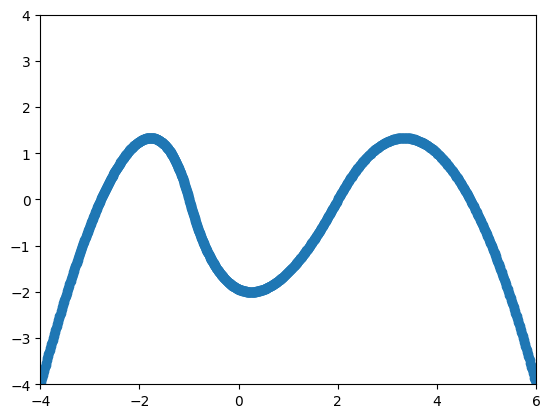
위의 이미지와 비교하면 거의 오차가 없는 것을 확인해 볼 수 있다.

안녕하세요. 포스팅 잘 봤습니다.
위의 예시를 이용해서 활용해보고 있는데요.
degree = 3 / control_point = 5개 / knots = 9개 / weight = 5 개로 변수를 구성할때,
point = point / accum_effective
에러가 발생하는데요. 무엇때문인지 알 수 있을까요?