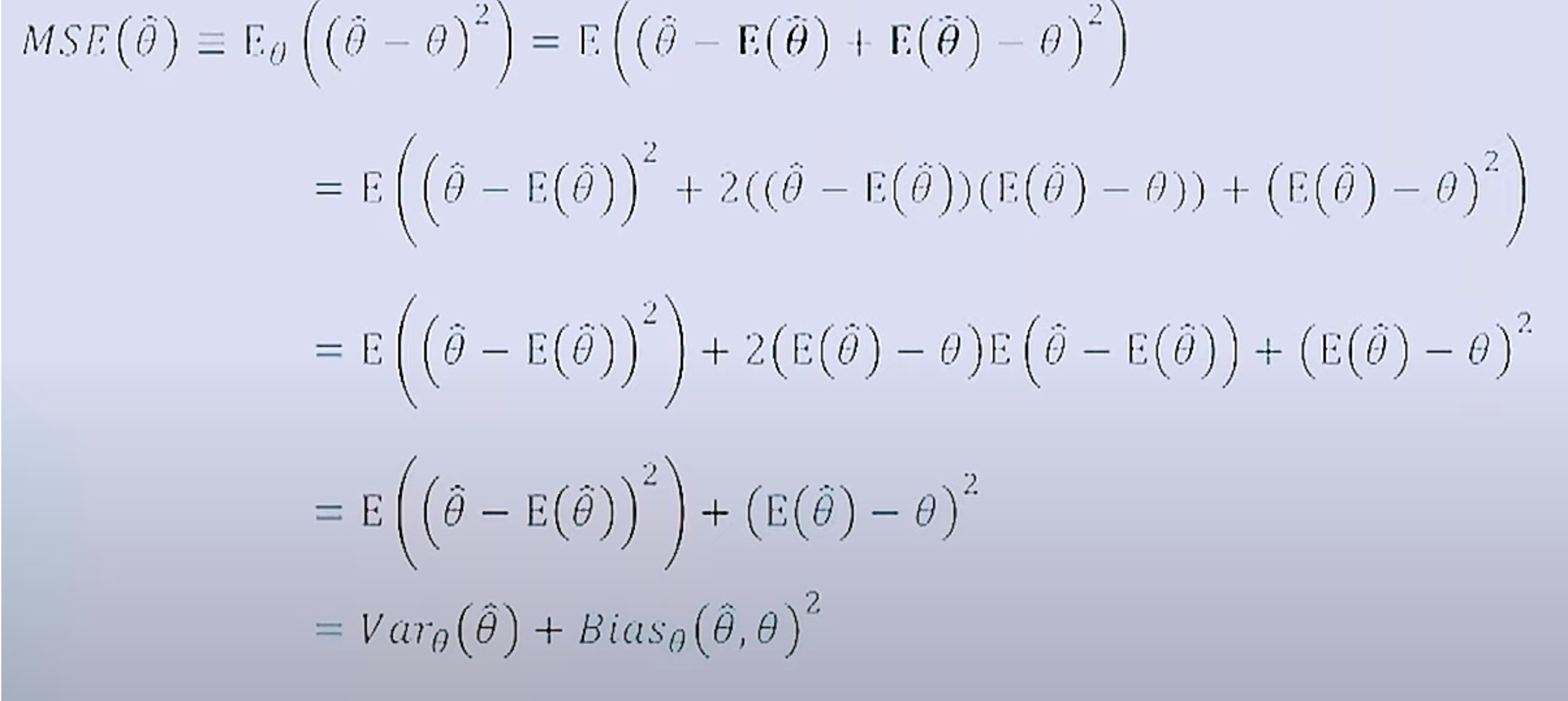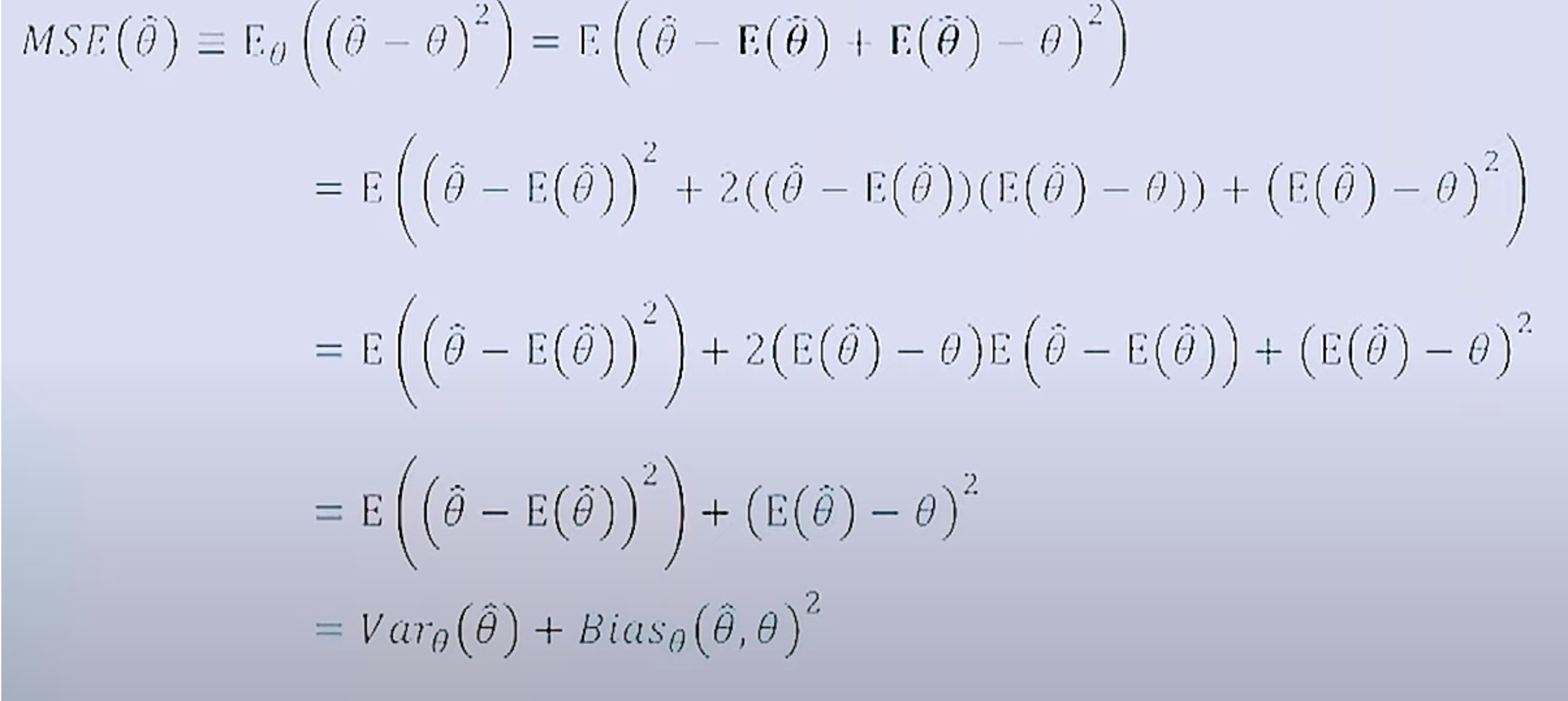
(ref: https://youtu.be/oyzIT1g1Z3U?si=1Z_e0T4jrlH9a5ak)

0. 개요

공부 중 MSE 전개에 대해 이해가 되지 않아서 세세하게 분석하여 정리함.

---

1. 전체 수식

${MSE}(\hat{\theta}) = E_{\theta}[(\hat{\theta} - \theta)^2] = E[(\hat{\theta} - E(\hat{\theta}) + E(\hat{\theta}) - \theta)^2]$

$= E[(\hat{\theta} - E[\hat{\theta}])^2 + 2(\hat{\theta} - E[\hat{\theta}])(E[\hat{\theta}] - \theta) + (E[\hat{\theta}] - \theta)^2]$

$= E[(\hat{\theta} - E[\hat{\theta}])^2] + 2(E[\hat{\theta}] - \theta)E[\hat{\theta} - E[\hat{\theta}]] + (E[\hat{\theta}] - \theta)^2$

1-a.

$\text{MSE}(\hat{\theta}) = E_{\theta}[(\hat{\theta} - \theta)^2] = E[(\hat{\theta} - E[\hat{\theta}] + E[\hat{\theta}] - \theta)^2]$

• $0 = - E[\hat{\theta}] + E[\hat{\theta}]$ 이기 때문에 중간에 삽입해도 결과값에 변화 없음.
• 치환할 경우 이 다음 라인 계산이 수월해짐.
  $E_{\theta}[(\alpha - \beta)^2]$
  • $\alpha = \hat{\theta} - E[\hat{\theta}]$
  • $\beta = E[\hat{\theta}] - \theta$

1-b.

원래 코드

${MSE}(\hat{\theta}) = E_{\theta}[(\hat{\theta} - \theta)^2]$
$= E[(\hat{\theta} - E(\hat{\theta}) + E(\hat{\theta}) - \theta)^2]$
$= E[(\hat{\theta} - E[\hat{\theta}])^2 + 2(\hat{\theta} - E[\hat{\theta}])(E[\hat{\theta}] - \theta) + (E[\hat{\theta}] - \theta)^2]$

치환하여 전개

${MSE}(\hat{\theta}) = E_{\theta}[(\hat{\theta} - \theta)^2]$
$= E[(\hat{\theta} - E(\hat{\theta}) + E(\hat{\theta}) - \theta)^2]$

• $\alpha = \hat{\theta} - E[\hat{\theta}]$
• $\beta = E[\hat{\theta}] - \theta$

$= E[(\alpha + \beta)^2]$
$= E[\alpha^2 + 2\alpha\beta + \beta^2]$
$= E[(\hat{\theta} - E[\hat{\theta}])^2 + 2(\hat{\theta} - E[\hat{\theta}])(E[\hat{\theta}] - \theta) + (E[\hat{\theta}] - \theta)^2]$

1-c.

$= E[(\hat{\theta} - E[\hat{\theta}])^2 + 2(\hat{\theta} - E[\hat{\theta}])(E[\hat{\theta}] - \theta) + (E[\hat{\theta}] - \theta)^2]$

$= E[(\hat{\theta} - E[\hat{\theta}])^2] + 2(E[\hat{\theta}] - \theta)E[\hat{\theta} - E[\hat{\theta}]] + (E[\hat{\theta}] - \theta)^2$

• $+ 2(E[\hat{\theta}] - \theta)E[\hat{\theta} - E[\hat{\theta}]] + (E[\hat{\theta}] - \theta)^2$
  => 해당 부분이 $E[]$ 에서 빠져나왔다.

• $2(E[\hat{\theta}] - \theta)E[\hat{\theta} - E[\hat{\theta}]]$
  $=2(E[\hat{\theta}] - \theta)(E[\hat{\theta}] - E[E[\hat{\theta}]])$ ※ 기대값의 성질 - 1
  $=2(E[\hat{\theta}] - \theta)(E[\hat{\theta}] - E[\hat{\theta}])$ ※기대값의 성질 - 2
  $=0$

• $(E[\hat{\theta}] - \theta)^2$
  해당 수식 자체가 bias 수식이기 때문에 이 자체로 상수 취급.
  그로 인해 기대값 성질에 의해 기대값에서 그대로 빠져 나올 수 있음.

※ 기대값의 성질 - 1
$E[X \pm Y] = E[X] \pm E[Y]$

※ 기대값의 성질 - 2
$E[C] = C$
$E[E[X]] = E[X]$
(E[X]는 그 자체로 결정된값. 상수이기 때문에 기대값의 기대값은 곧 기대값이 된다.)

(ref: https://m.blog.naver.com/running_p/90178494167)

1-d.

$= E[(\hat{\theta} - E[\hat{\theta}])^2] + 2(E[\hat{\theta}] - \theta)E[\hat{\theta} - E[\hat{\theta}]] + (E[\hat{\theta}] - \theta)^2$
$= E[(\hat{\theta} - E[\hat{\theta}])^2]+(E[\hat{\theta}] - \theta)^2$
$= \text{Var}_{\theta}(\hat{\theta}) + \text{Bias}_{\theta}(\hat{\theta}, \theta)^2$

• $\text{Var}_{\theta}(\hat{\theta}) = E[(\hat{\theta} - E[\hat{\theta}])^2]$
• $\text{Bias}_{\theta}(\hat{\theta}, \theta) = E[\hat{\theta}] - \theta$

---

2. 결론

• $\text{MSE}(\hat{\theta}) = \text{Var}_{\theta}(\hat{\theta}) + \text{Bias}_{\theta}(\hat{\theta}, \theta)^2$
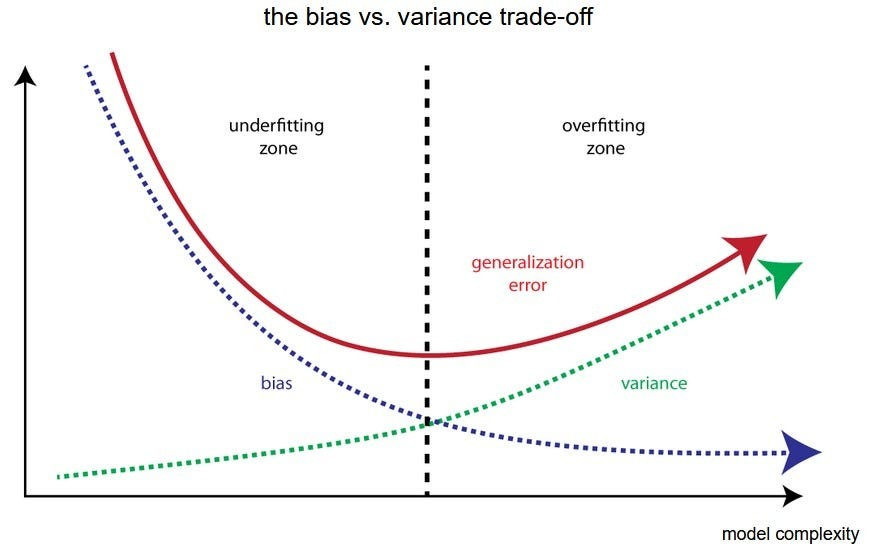
  • bias-variance tradeoff: bias와 variance는 상충 관계.(하나가 상승하면 다른 하나가 하락하는 관계)

• Variance(분산): 데이터의 다양성에 얼마나 민감한지에 대한 척도
  • V↑: 훈련데이터의 작은 변화에도 크게 반응 (overfitting)
• Bias(편향): 모델, 추정치가 실제 문제를 얼마나 잘 일반화지에 대한 척도
  • B↑: 모델이 너무 단순하여 데이터 중요성을 포착 불가 (underfitting)

• 복잡한 모델(V↑ B↓): 훈련 데이터의 노이즈까지 학습. 그로 인해 새로운 데이터에 대한 예측이 불안정.
• 복잡한 모델(V↓ B↑): 훈련 데이터의 노이즈에 덜 민감하지만 그로 인해 중요한 패턴을 놓칠 수 있음.
• 최적의 모델(V↓ B↓): 편향과 분산이 모두 낮은 상태. 이를 달성하기 위해서는 데이터와 문제에 적합한 모델 복잡도를 찾아야 한다.

(ref: https://www.linkedin.com/pulse/bias-variance-tradeoff-sanjay-kumar-mba-ms-phd/)

(ref: https://medium.com/@ivanreznikov/stop-using-the-same-image-in-bias-variance-trade-off-explanation-691997a94a54)

---

ref

1. https://youtu.be/oyzIT1g1Z3U?si=1Z_e0T4jrlH9a5ak
2. https://m.blog.naver.com/running_p/90178494167
3. https://www.linkedin.com/pulse/bias-variance-tradeoff-sanjay-kumar-mba-ms-phd/
4. https://medium.com/@ivanreznikov/stop-using-the-same-image-in-bias-variance-trade-off-explanation-691997a94a54